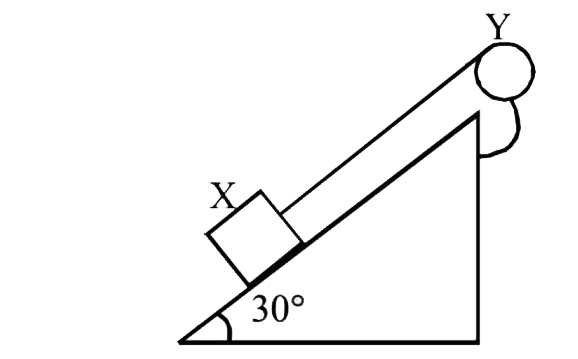
A block X of mass 0.5 kg is held by a long massless string on a frictionless inclined plane of inclination 30∘ to the horizontal. The string is wound on a uniform solid cylindrical drum Y of mass 2kg and of radius 0.2m as shown in Fingure. The drum is given an initial angular velocity such that the block X starts moving up the plane.
(i) Find the tension in the string during the motion.
(ii) At a certain instant of time the magnitude of the angular velocity of Y s 10rads−1 calculate the distance travelled by X from that instant of time until it comes to rest
a. i. First Method: "Force/ Torque" Method:
Force equation for the block are as follows:
N−5cos30∘=0………..i
5sin30∘−T=0.5×a…………..ii
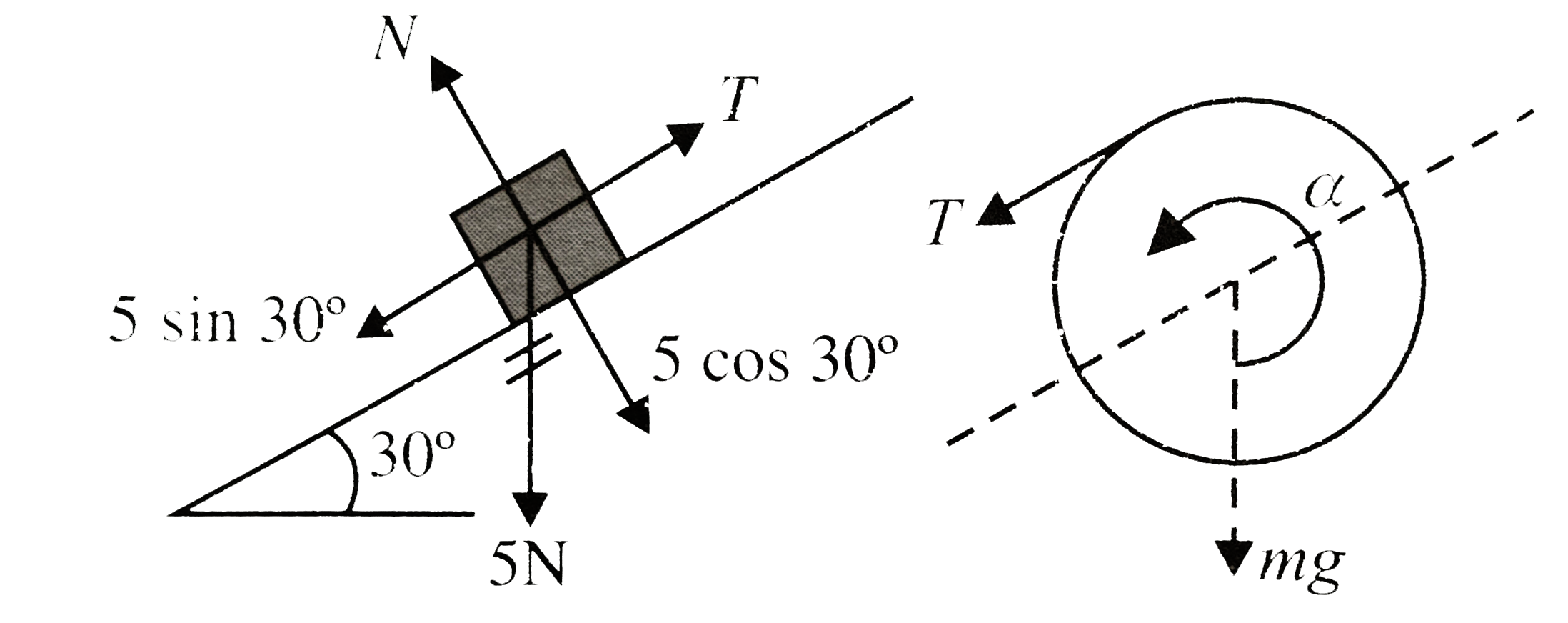
Torque equatioin for the drum
TR=(12MR2)α
⇒T=12MRα=12×2×0.2α⇒t=0.2α..........iii
Here a=Rα (The string does not slip on the drum)
Thus T=(0.2)(aR)=0.2(a0.2)=1×a .......i
From eqn ii and iv we get
a=53ms,T=53N
ii. Second Method: Using the equation →τ=−→dLdt
Take both block X and drum Y as a system.
Torque acting on the system about the centre of mass of the drum =(mgsin30∘)R, anticlockwise . Angular momentum of the system about the centre of mass of the drum,
L=mvR+12MR2ω
=m(rω)R+12MR2ω
=(mR2+12MR2)ω, clockwise
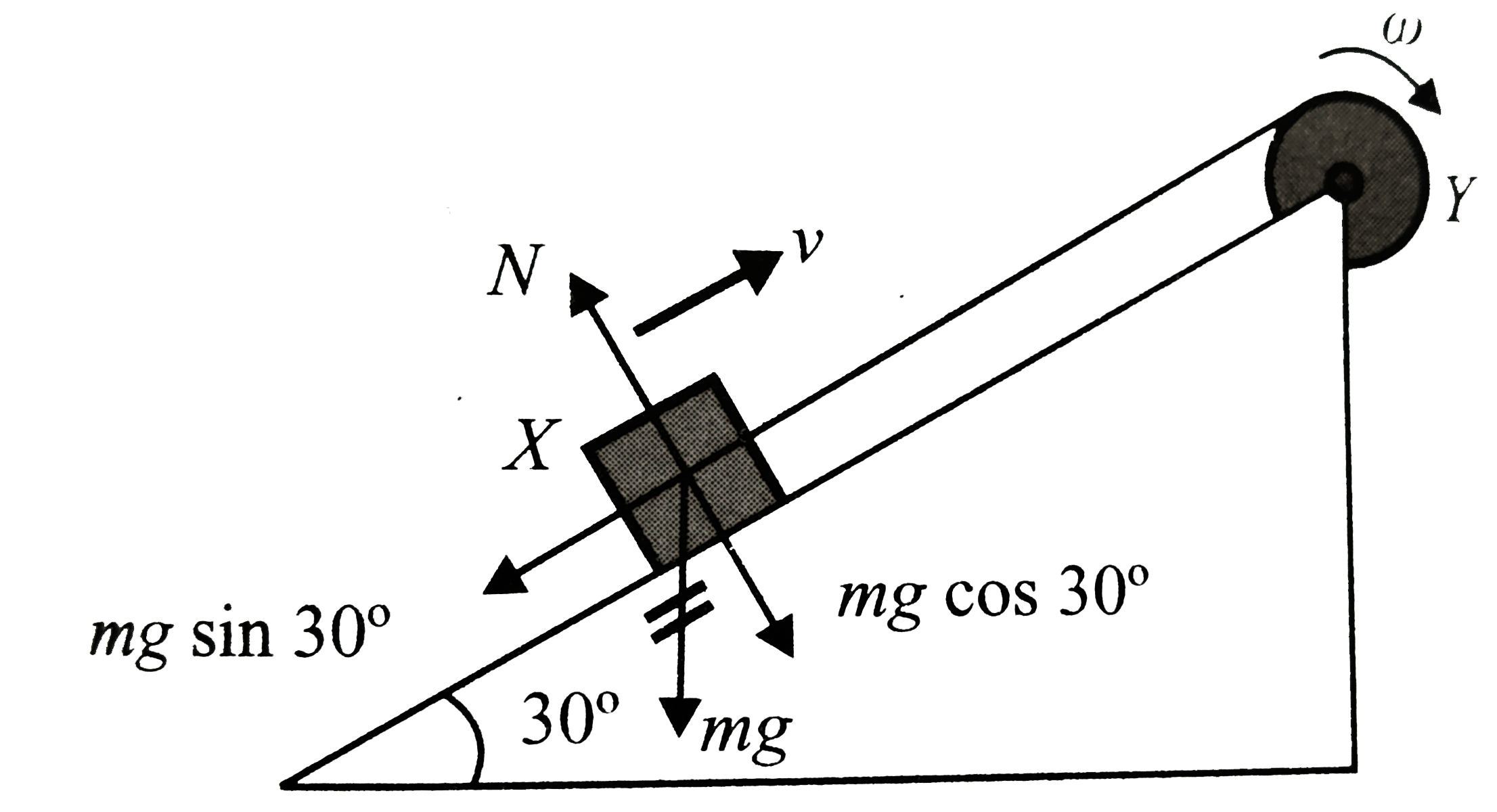
Apply equation →τ=−→dLdt
−mgRsin30∘=ddt(mR2ω+12MR2ω)
=(mR2+12MR2)dωdt
⇒dωdt=−mgRsin30∘(mR2+MR22)
⇒(dωdt)aniticlockwise
=mgRsin30∘(mR2+MR22)
(ω has been taken in the clockwise sennse dωdt is negative.
So, dωdt is in the anticlockwise sense).
clearly, τ=IαTR=I(dωdt)anticlock
=(12MR2)⎛⎝mgRsin30∘m+M2⎞⎠=53N
b. i. First method:
Angular velocity of Y=10rad/s
Velocity fo block X=Rω=0.2×10=2m/s, along the plane upwards
Acceleration of X=53ms2 along the plane downwards
Using equation v2=u2−2as,
02=(2)−2×53×s⇒s=4×32×5=1.25m
ii Second Method:
You can also calculate the distance X moves upwards from the energy considerations
WN+Wmg+Wf+Wmg=K2−K1
0−(mgsinθ)s+0+0=(12mv2+12IΩ2)
⇒(mgsinθ)s=12mv2+12Iω2
∴s=mv2+Iω22mgsinθs
=(0.5)(2)2+2×2×(0.2)2×(10)22x0.5×10×12=1.2m
iii. Third Method: By Mechanical Energy Conservation
Here the only force which does work on the system mg, the algebraic work done by other forces is zeros, is conservative in nature, therefore, the mechanical energy of the system will remain constant. Let the distance moved by the block X along the plane be s.
Gain in gravitational potential energy of X=mgssinθ.
Loss in kinetic energy of the block and the drum is
12mv20+12Iω20(v0=ω0r)
Thus, mgssinθ=12mv20+12Iω20
s=mv20+Iω202mgsiθ
After substituting the given values s=1.02m
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.1
11 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.2
13 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
A block of mass 10 kg is kept on a fixed rough (μ=0.8) inclined plane of angle of inclination 30∘. The frictional force acting on the block is

View SolutionA person pushes a block of mass 4 kg up a frictionless inclined plane 10 m long and that makes an angle of 30∘ with the horizontal . Then the work done is
View SolutionA block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
View SolutionA block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
View SolutionA block of mass 4 kg is pulled along a smooth inclined plane of inclination 30∘ with constant velocity 3 m/s as shown, power delivered by the force is
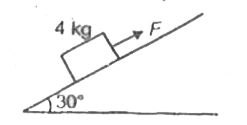
View SolutionA block of mass 30 kg is suspended by three string as shown in fig, Find the tension in each string.

View SolutionA block of mass 5 kg is at rest on a rough inclined surface. If angle of inclination of plane is 60∘, then force applied by it on block is
View SolutionA block of mass 2 kg rests on a rough inclined plane making an angle of 30° with the horizontal. If μS=0.6 , what is the frictional force on the block ?
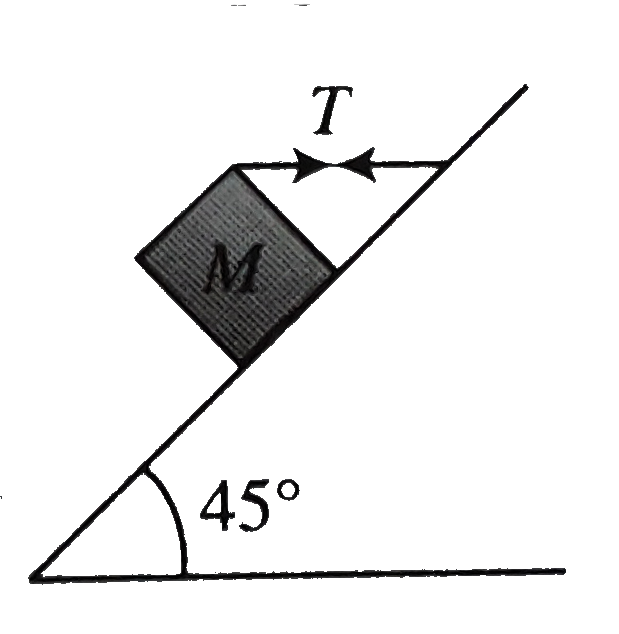
View SolutionA block of mass 15kg is resting on a rough inclined plane as shown in figure ,The block is tied by a horizontal string which has a tension 50N The coefficient of contact is
View SolutionA block of mass 5.0 kg slides down an incline of inclination 300 and length 10 m. find the work done by the force of gravity.
View Solution
