A body is projected with a speed 160 m/s at an angle 53∘ with the horizontal, At the highest point, body explodes into two pieces with mass ratio 1:3. Smaller piece comes to rest immediately after explosion. Find the distance of point from point of projection where heavier piece strikes the horizontal surface.
To solve the problem step by step, we will follow the procedure outlined in the video transcript.
Step 1: Identify the given data
- Initial speed u=160m/s
- Angle of projection θ=53∘
- Mass ratio of the two pieces after explosion m1:m2=1:3
Step 2: Calculate the range of the projectile before the explosion
The formula for the range R of a projectile is given by:
R=u2sin(2θ)g
Where:
- g=10m/s2 (acceleration due to gravity)
First, we calculate sin(2θ):
sin(2×53∘)=sin(106∘)≈0.961
Now substituting the values into the range formula:
R=(160)2⋅0.96110
R=25600⋅0.96110=2456.96m≈2160m
Step 3: Understand the explosion and the motion of the pieces
At the highest point of the projectile's motion, the body explodes into two pieces:
- The smaller piece (mass m1) comes to rest immediately after the explosion.
- The heavier piece (mass m2) continues to move.
Step 4: Calculate the center of mass of the system
Since the smaller piece comes to rest, the center of mass of the system will continue to follow the same trajectory as before the explosion. The center of mass Xcm can be calculated as:
Xcm=m1x1+m2x2m1+m2
Where:
- m1=M4 (smaller piece)
- m2=3M4 (heavier piece)
- x1=R/2=1080m (distance covered by the smaller piece)
Step 5: Solve for the distance x2 of the heavier piece
Substituting the known values into the center of mass equation:
2160=(M4)⋅1080+(3M4)x2M
This simplifies to:
2160=270M+3M4x2M
2160=270+34x2
Now, isolating x2:
2160−270=34x2
1890=34x2
Multiplying both sides by 43:
x2=1890⋅43=2520m
Final Result
The distance from the point of projection where the heavier piece strikes the horizontal surface is:
2520m
- Initial speed u=160m/s
- Angle of projection θ=53∘
- Mass ratio of the two pieces after explosion m1:m2=1:3
The formula for the range R of a projectile is given by:
R=u2sin(2θ)g
Where:
- g=10m/s2 (acceleration due to gravity)
sin(2×53∘)=sin(106∘)≈0.961
R=(160)2⋅0.96110
R=25600⋅0.96110=2456.96m≈2160m
At the highest point of the projectile's motion, the body explodes into two pieces:
- The smaller piece (mass m1) comes to rest immediately after the explosion.
- The heavier piece (mass m2) continues to move.
Since the smaller piece comes to rest, the center of mass of the system will continue to follow the same trajectory as before the explosion. The center of mass Xcm can be calculated as:
Xcm=m1x1+m2x2m1+m2
Where:
- m1=M4 (smaller piece)
- m2=3M4 (heavier piece)
- x1=R/2=1080m (distance covered by the smaller piece)
Substituting the known values into the center of mass equation:
2160=(M4)⋅1080+(3M4)x2M
This simplifies to:
2160=270M+3M4x2M
2160=270+34x2
Now, isolating x2:
2160−270=34x2
1890=34x2
Multiplying both sides by 43:
x2=1890⋅43=2520m
The distance from the point of projection where the heavier piece strikes the horizontal surface is:
2520m
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - NCERT FILE ( NCERT TEXTBOOK EXERCISES )
21 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - NCERT FILE ( NCERT (ADDITIONAL EXERCISES) )
12 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Conceptual Questions
24 Videos
- PHYSICAL WORLD BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)
6 Videos
- THERMAL PROPERTIES OF MATTERBOOK - MODERN PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
A body is projected at angle of 45∘ to the horizontal . What is its velocity at the highest point ?
View SolutionA projectile is fired at a spedd of 100 m/s at an angel of 370 above the horizontal. At the highest point, the projectile breaks into two parts of mass ratio 1:3 the smaller coming to rest. Findthe distance from the launching point to the where the heavier piece lands.
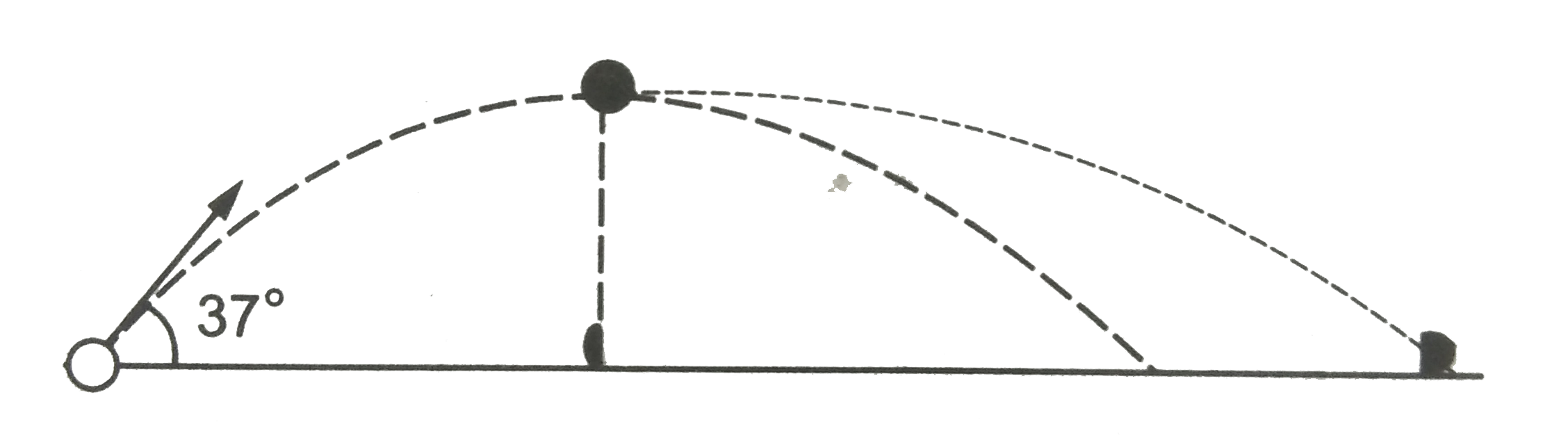
View Solution
Knowledge Check
A body of mass m is projected with intial speed u at an angle θ with the horizontal. The change in momentum of body after time t is :-
Am u sinθB2 m u sinθCm g tDzeroA stone is projected with speed of 50ms−1 at an angle of 60∘ with the horizontal. The speed of the stone at highest point of trajectory is
A75ms−1B25ms−1C50ms−1Dcannot findA body is projected at an angle of 30∘ with the horizontal with momentum P.At its highest point the magnitude of the momentum is:
A√32PB2√3PCPDP2
A projectile of mass "m" is projected from ground1 with a speed of 50 m/s at an angle of 53∘ with the horizontal. It breaks up into two equal parts at the highest point of the trajectory. One particle coming to rest immediately after the explosion.
The distance between the pieces of the projectile when they reach the ground are :
View SolutionA body is projected with a speed (u) at an angle to the horizontal to have maximum range. What is its velocity at the highest point ?
View SolutionA body is projected with speed u at an angle θ to the horizontal to have maximum range. Its velocity at the highest point will be ___.
View SolutionA bullet fired from gun with a velocity 30 m/s at an angle of 60∘ with horizontal direction. At the highest point of its path, the bullet explodes into two parts with masses in the ratio 1 : 3. The lighter mass comes to rest immediately. Then the speed of the heavier mass is
View SolutionA bomb of mass m is projected from the ground with speed v at angle θ with the horizontal. At the maximum height from the ground it explodes into two fragments of equal mass. If one fragment comes to rest immediately after explosion, then the horizontal range of centre of mass is
View Solution
