A body moves under the action of a constant force along a straight line. The instantaneous power developed by this force with time t is correctly represented by.
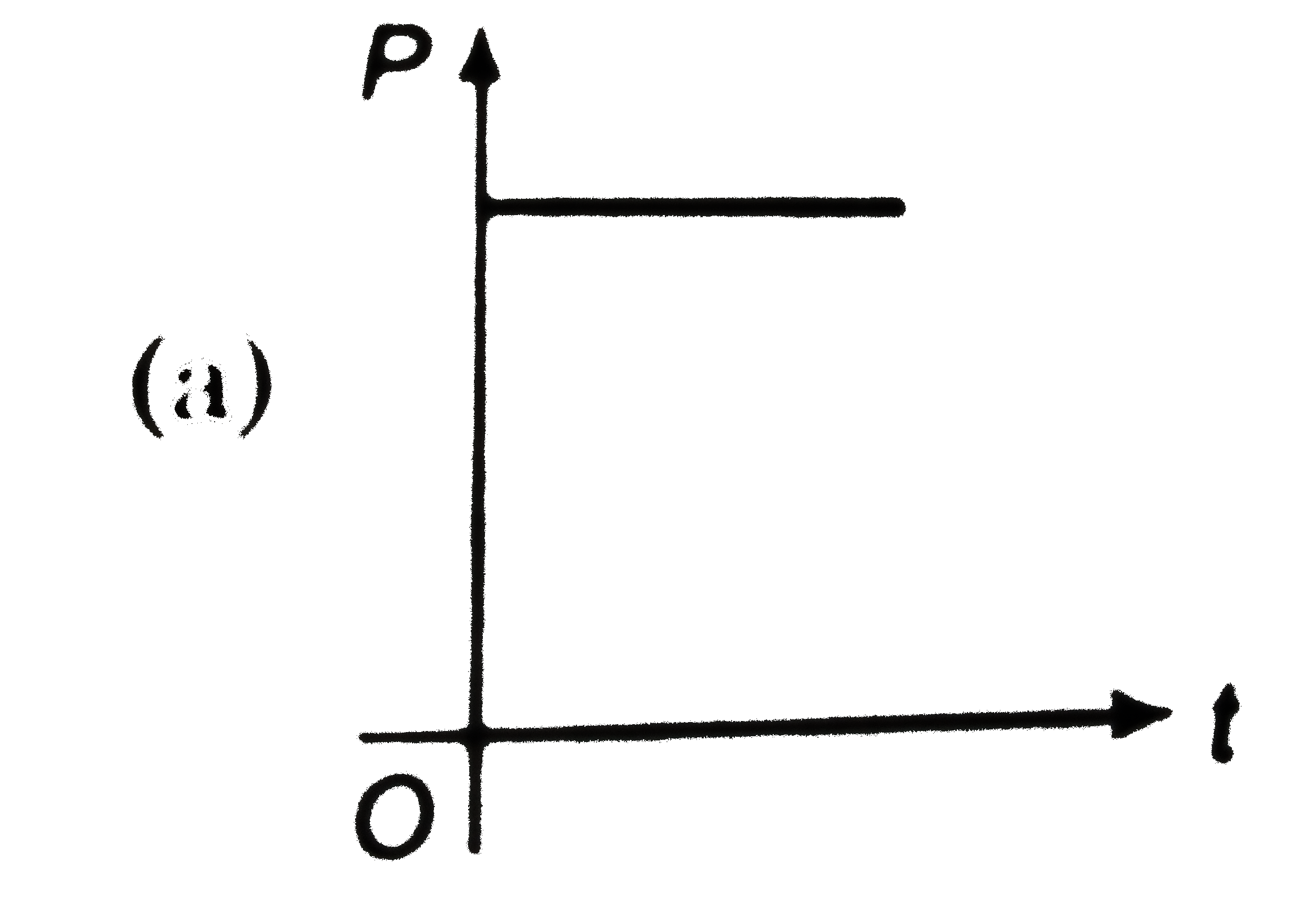
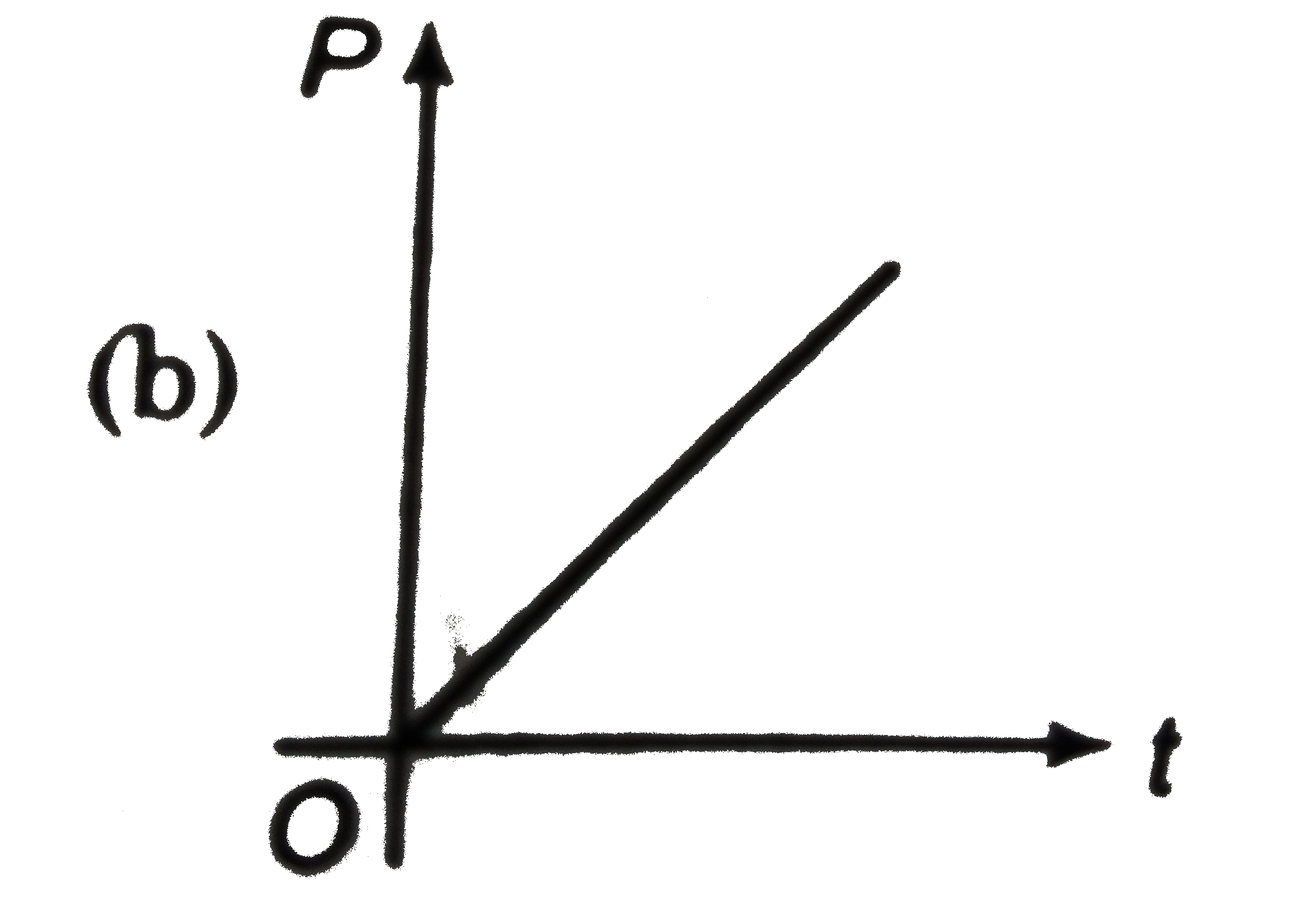
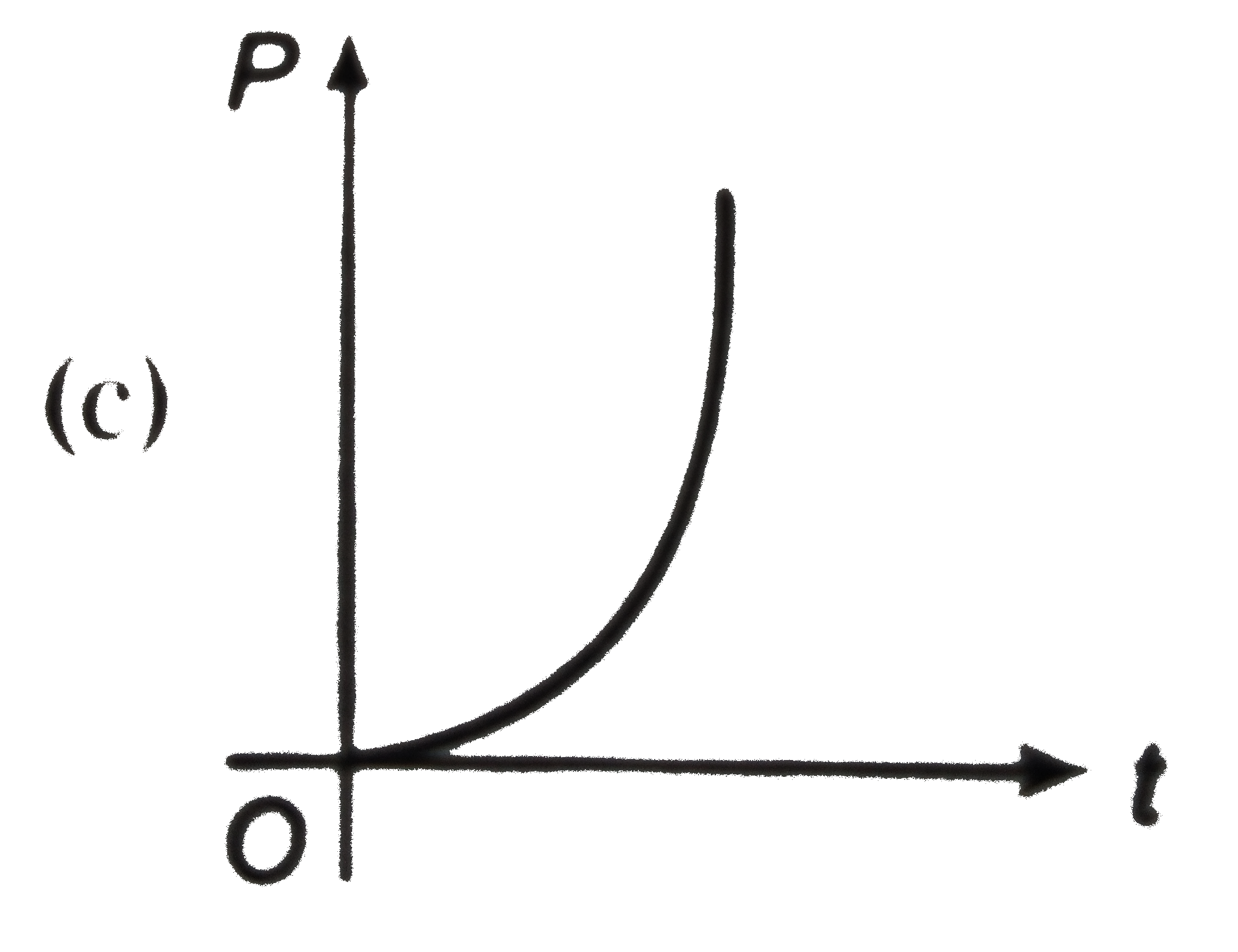

The correct Answer is:B
To solve the problem of determining how instantaneous power developed by a constant force changes with time, we can follow these steps:
Step 1: Understand the relationship between power, force, and velocity
The instantaneous power P developed by a force F acting on a body is given by the equation:
P=F⋅V
where V is the velocity of the body.
Step 2: Analyze the motion under constant force
Since the body is moving under the action of a constant force along a straight line, we know that the force F is constant. The acceleration a of the body can be expressed as:
a=Fm
where m is the mass of the body.
Step 3: Relate velocity to time
If the body starts from rest, the velocity V of the body at time t can be expressed as:
V=a⋅t=(Fm)⋅t
Step 4: Substitute the expression for velocity into the power equation
Now, substituting the expression for velocity V into the power equation:
P=F⋅V=F⋅(Fm⋅t)
This simplifies to:
P=F2m⋅t
Step 5: Analyze the relationship between power and time
From the equation P=F2m⋅t, we can see that power P is directly proportional to time t. This indicates that as time increases, the power also increases linearly.
Conclusion
The instantaneous power developed by the constant force with time t is represented by a linear function of time. Therefore, the correct option is:
Option B.
---
The instantaneous power P developed by a force F acting on a body is given by the equation:
P=F⋅V
where V is the velocity of the body.
Since the body is moving under the action of a constant force along a straight line, we know that the force F is constant. The acceleration a of the body can be expressed as:
a=Fm
where m is the mass of the body.
If the body starts from rest, the velocity V of the body at time t can be expressed as:
V=a⋅t=(Fm)⋅t
Now, substituting the expression for velocity V into the power equation:
P=F⋅V=F⋅(Fm⋅t)
This simplifies to:
P=F2m⋅t
From the equation P=F2m⋅t, we can see that power P is directly proportional to time t. This indicates that as time increases, the power also increases linearly.
The instantaneous power developed by the constant force with time t is represented by a linear function of time. Therefore, the correct option is:
Option B.
Topper's Solved these Questions
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 1 subjective
27 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Objective
30 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 1 Assertion And Reason
12 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question
11 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
Similar Questions
Under the action of a constant force, A particle is experiencing a constant acceleration. The power is
View SolutionA motor drives a body along a straight line with a constant force. The power P developed by the motor must vary with time t as
View SolutionA particle is moving with a constant speed along a straight line path. A force is not required to
View SolutionA particle moves under the action of a force F=20ˆi+15ˆj along a straight line 3y+αx=5, where, α is a constant. If the work done by the force F is zero the value of α is .
View SolutionA body starts from rest and acquires velocity V in time T. The instantaneous power delivered to the body in time 't' proportional to
View SolutionFor a body moving with uniform acceleration along straight line, the variation of its velocity (v) with position (x) is best represented by
View SolutionA particle moves with a velocity v=(5ˆi−3ˆj+6ˆk)ms−1 under the influence of a constant force
F=(10ˆi+10ˆj+20ˆh)N, the instantaneous power applied to the particle is.
View SolutionA particle moves with a velocity v=(5ˆi−3ˆj+6ˆk)ms−1 under the influence of a constant force
F=(10ˆi+10ˆj+20ˆh)N, the instantaneous power applied to the particle is.
View SolutionA particle moves with a velocity of (4ˆi−2ˆj+2ˆk)ms−1 under the influence of a constant force →F=(10ˆi+3ˆj−2ˆk)N. The instantaneous power applied to the particle is
View SolutionA body is moved along a straight line by a machine delivering constant power . The distance moved by the body is time t is proptional to
View Solution
