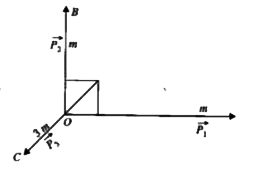
A body of mass 1 kg is initially at rest. It explodes into three pieces of masses in the ratio . Two pieces of equal masses fly off perpendicular to each other with a speed of . What is the velocity of the heavier mass ?
Let the mass of the three fragments be m kg, m kg, and 3m kg.
Total mass = 1kg
So
Momentum along OA is Mass Velocity
v velocity of the 3rd piece.
Total momentum after collision = Total momentum before collision. Initially 1kg was at rest.
Magnitude of
Topper's Solved these Questions
- BOOK - ICSECHAPTER - DYNAMICSEXERCISE - CONCEPTUAL SHORT ANSWER QUESTIONS WITH ANSWERS20videos
DYNAMICS
- BOOK - ICSECHAPTER - DYNAMICSEXERCISE - SHORT ANSWER QUESTIONS93videos
DYNAMICS
- BOOK - ICSECHAPTER - DYNAMICSEXERCISE - SHORT ANSWER QUESTIONS WITH ANSWERS12videos
DYNAMICS
- BOOK - ICSECHAPTER - DIMENSIONSEXERCISE - SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)9videos
DIMENSIONS
- BOOK - ICSECHAPTER - FRICTIONEXERCISE - Selected problems30videos
FRICTION
Similar Questions
A body of mass 1kg initially at rest explodes and breaks into threee fragments of masses in the ratio 1:1:3. The two pieces of equal masses fly off perpendicular to each other with a speed of 30m/s each What is the velocity of heavier fragments ? .
View SolutionA bomb of mass 5m initially at rest explodes and breaks into three pieces of masses in the ratio 1:1:3. The two pieces of equal mass fly off perpendicular to each other with a speed of v0. What is the velocity of the heavier piece? Also , calculate the energy released in explosion.
View Solution
Knowledge Check
- Question 1 - Select One
A body of mass 1kg initially at rest, explodes and breaks into three fragments of masses in the ratio 1:1:3. The two pieces of equal mass fly off perpendicular to each other with a speed of 15ms−1 each. What is the velocity of the heavier fragment?
A10√ms−1B5√3ms−1C10√3ms−1D5√2ms−1 - Question 2 - Select One
A body of mass 1kg initially at rest explodes and breaks into three parts of masses in the ration 1:2:3. If the two pieces of equal masses fly off perpendicular to each other with a speed of 30m/s The speed of third piece will be .
A10√2m/sB20√2m/sC5√2m/sD40√2m/s - Question 3 - Select One
A body of mass 5 kg explodes at rest into three fragments with masses in the ratio 1 : 1 : 3. The fragments with equal masses fly in mutually perpendicular directions with speeds of 21 m/s. The velocity of the heaviest fragment will be -
A11.5 m/sB14.0 m/sC7.0 m/sD9.89 m/s
A body of mass 1 kg initially at rest explodes and breaks into three fragments of masses in the ratio 1: 1: 3. The two pieces of equal mass fly off perpendicular to each other with a speed of 30ms−1 each. What is velocity of the heavier fragment?
View SolutionA body of mass 1kg initially at rest, explodes and breaks into three fragments of masses in the ratio 1:1:3. The two pieces of equal mass fly off perpendicular to each other with a speed of 15ms−1 each. What is the velocity of the heavier fragment?
View SolutionA body of mass 1 kg at rest explodes into three fragments of masses in the ratio 1 : 1 : 3 . The two pieces of equal mass fly in mutually perpendicular directions with a speed of 30m/s each . What is the velocity of the heavier fragment ?
View SolutionA body of mass 1kg initially at rest explodes and breaks into threee fragments of masses in the ration breaks into three fragments of masses in the ration 1:1:3. The two pieces of equal masses fly off perpendicular to each other with a speed of 30m/s each What is the velocity of heavier fragments ? .
View SolutionA body of mass 5 kg explodes at rest into three fragments with masses in the ratio 1 : 1 : 3. The fragments with equal masses fly in mutually perpendicular directions with speeds of 21 m/s . The velocity of the heaviest fragment will be
View Solution
