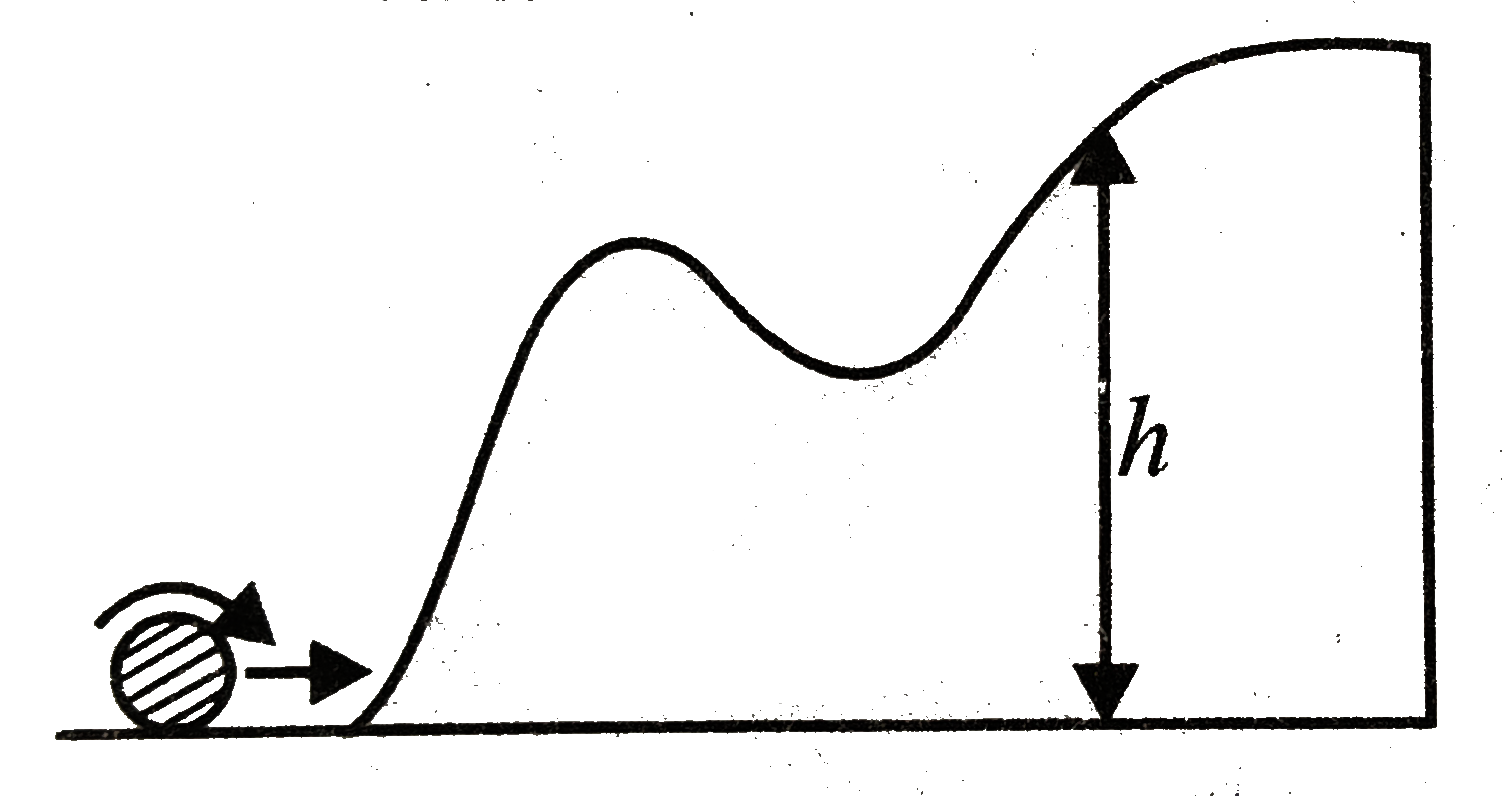
A body of mass $M$ and radius $r$ , rolling on a smooth horizontal floor with velocity $v$ , rolls up an irregular inclined plane up to a vertical height $(3 v^{2} / 4 g)$ . Compute the moment of inertia of the body.

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $\frac{M r^{2}}{2}$

The total kinetic energy of the body
$K = K_{T} = K_{R} = \frac{1}{2} M v^{2} + \frac{1}{2} I ω^{2}$
$= \frac{1}{2} M v^{2} [1 + (\frac{M}{M r^{2}})]$ [as $v = r ω]$
when it rolls up an iregular inclined plane of height $(h = 3 \frac{v^{2}}{4} g)$ , its $K E$ is converted into $P E$ , so by conservation of mechanical energy
$\frac{1}{2} M V^{2} [= 1 + \frac{1}{M r^{2}}] = M g [\frac{3 v^{2}}{4 g}]$
Which on simplification gives $I = \frac{M r^{2}}{2}$ . This result clearly indicates that the body is either a disc or a cylinder.

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A loop of mass M and radius R is rolling on a smooth horizontal surface with speed 'v'. It's total kinetic energy is
A $1 / 2 M v^{2}$
B $3 / 2 M v^{2}$
C $M v^{2}$
D $1 / 2 M R^{2} ω^{2}$
Question 2 - Select One
A body of mass M and radius R is rolling horizontally without slipping with speed v . It then rolls up a hill to a maximum height h . If $h = \frac{5 v^{2}}{6 g}$ , what is the M.I of the body ?
A $\frac{M R^{2}}{2}$
B $\frac{2}{3} M R^{2}$
C $\frac{3}{4} M r^{2}$
D $\frac{2}{5} M R^{2}$
Question 3 - Select One
An object of radius R and mass M is rolling horizontally without slipping with speed v . It then rolls up the hill to a maximum height $h = \frac{3 v^{2}}{4 g}$ . The moment of inertia of the object is ( g = acceleration due to gravity)
A $\frac{2}{5} M R^{2}$
B $\frac{M R^{2}}{2}$
C $M R^{2}$
D $\frac{3}{2} M R^{2}$

CENGAGE PHYSICS-RIGID BODY DYNAMICS 2-Subjective

Home
Ask Doubt
Profile