A body of mass m is placed on a rough surface with coefficient of friction μ inclined at θ. If the mass is in equilibrium , then
θ=tan−1μ
θ=tan−1(1μ)
θ=tan−1(m)μ
θ=tan−1(μ)m
The correct Answer is:A
To solve the problem step by step, we will analyze the forces acting on the body placed on the inclined plane and derive the relationship between the angle of inclination, the coefficient of friction, and the equilibrium condition.
1. Identify the Forces Acting on the Body:
- The weight of the body (mg) acts vertically downward.
- The weight can be resolved into two components:
- Perpendicular to the incline: mgcosθ
- Parallel to the incline: mgsinθ
2. Determine the Normal Force:
- The normal force (N) acts perpendicular to the surface of the incline.
- In equilibrium, the normal force balances the perpendicular component of the weight:
N=mgcosθ
3. Determine the Frictional Force:
- The frictional force (f) acts up the incline to counteract the component of the weight acting down the incline.
- The maximum static frictional force can be expressed as:
f=μN
- Substituting for N, we get:
f=μ(mgcosθ)
4. Set Up the Equilibrium Condition:
- Since the body is in equilibrium, the frictional force must balance the component of the weight acting down the incline:
mgsinθ=f
- Substituting for f, we have:
mgsinθ=μ(mgcosθ)
5. Simplify the Equation:
- We can cancel out mg from both sides (assuming m ≠ 0):
sinθ=μcosθ
6. Rearranging the Equation:
- Dividing both sides by cos θ gives:
tanθ=μ
7. Finding the Angle θ:
- Therefore, we can express θ in terms of the coefficient of friction:
θ=tan−1(μ)
Final Answer:
The angle of inclination θ is given by:
θ=tan−1(μ)
- The weight of the body (mg) acts vertically downward.
- The weight can be resolved into two components:
- Perpendicular to the incline: mgcosθ
- Parallel to the incline: mgsinθ
- The normal force (N) acts perpendicular to the surface of the incline.
- In equilibrium, the normal force balances the perpendicular component of the weight:
N=mgcosθ
- The frictional force (f) acts up the incline to counteract the component of the weight acting down the incline.
- The maximum static frictional force can be expressed as:
f=μN
- Substituting for N, we get:
f=μ(mgcosθ)
- Since the body is in equilibrium, the frictional force must balance the component of the weight acting down the incline:
mgsinθ=f
- Substituting for f, we have:
mgsinθ=μ(mgcosθ)
- We can cancel out mg from both sides (assuming m ≠ 0):
sinθ=μcosθ
- Dividing both sides by cos θ gives:
tanθ=μ
- Therefore, we can express θ in terms of the coefficient of friction:
θ=tan−1(μ)
The angle of inclination θ is given by:
θ=tan−1(μ)
Topper's Solved these Questions
- LAWS OF MOTIONBook:DC PANDEY ENGLISHChapter:LAWS OF MOTIONExercise:Match the columns
Explore 7 Videos
- KINEMATICS 1Book:DC PANDEY ENGLISHChapter:KINEMATICS 1Exercise:INTEGER_TYPE
Explore 15 Videos
- LAWS OF THERMODYNAMICSBook:DC PANDEY ENGLISHChapter:LAWS OF THERMODYNAMICSExercise:Level 2 Subjective
Explore 18 Videos
Similar Questions
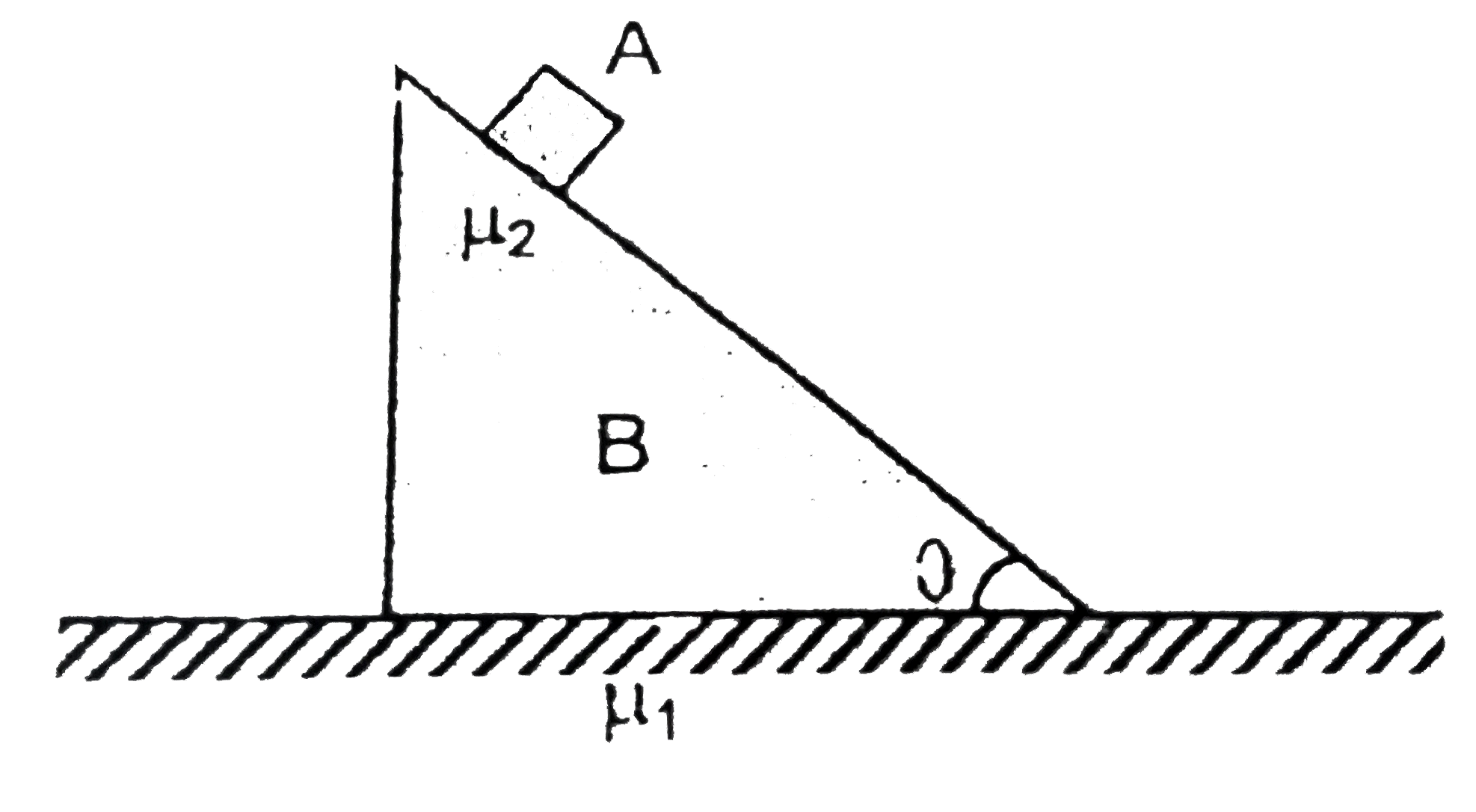
A wedge B of mass 2 m is placed on a rough horizontal suface. The coefficient of friction between wedge and the horizontal surface is μ1. A block of mass m is placed on wedge as shown in the figure. The coefficient of friction between block and wedge is μ2. The block and wedge are released from rest.
Q. Suppose the inclined surface of the wedge is at θ=37∘ from angle from horizontal and μ2=0 are wedge will remain in equilibrium if
View Solution
A wedge B of mass 2 m is placed on a rough horizontal suface. The coefficient of friction between wedge and the horizontal surface is μ1. A block of mass m is placed on wedge as shown in the figure. The coefficient of friction between block and wedge is μ2. The block and wedge are released from rest.
Q. Suppose the inclined surface of the wedge is at θ=37∘ from angle from horizontal and μ2=0 are wedge will remain in equilibrium if
View Solution
Knowledge Check
A block of mass 10kg is placed on a rough horizontal surface having coefficient of friction μ=0.5 . If a horizontal force of 100N is acting on it, then acceleration of the block will be.
A10ms−2B5ms−2C15ms−2D0.5ms−2
A block of mass m is pulled on an incline surface having coefficient of friction μ=1& angle of inclination θ=30∘, with the horizontal, such that required external force is minimum. The angle made by this force with the incline is :
View SolutionA block of mass 10kg is placed on a rough horizontal surface having coefficient of friction μ=0.5 . If a horizontal force of 100N is acting on it, then acceleration of the will be.
View SolutionA block of mass 10kg is placed on a rough horizontal surface having coefficient of friction μ=0.5 . If a horizontal force of 100N is acting on it, then acceleration of the will be.
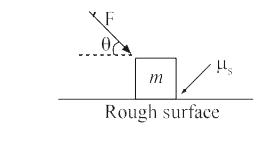
View SolutionWhat is the value of applied force ‘F’ which is exerted at an angle θ with the horizontal on a block of mass ‘m’ placed on a horizontal rough surface, if the coefficient of static friction between the block and the surface is , such that the block is on the verge of moving horizontally?
View SolutionA block of mass 10kg is placed on a rough horizontal surface having coefficient of friction μ=0.5 . If a horizontal force of 100N is acting on it, then acceleration of the block will be.
View SolutionA block of mass 10 kg is placed on a rough horizontal surface of coefficient of friction 0.1. A pulling force of 100 N acts on it at 37∘ with the horizontal. The frictional force acting on the body is ..... N.
View SolutionA block of mass m is attached with a massless spring of force constant K. the block is placed over a rough inclined surface for which the coefficient of friction is μ=34 find the minimum value of M required to move the block up the place. (Neglect mass of string and pulley. Ignore friction in pulley).
 .
.
View Solution