A lift is moving downwards with an acceleration equal to g. A block of mass m , kept on the floor of the lift of friction coefficient μ , is pulled horizontally . The friction acting on the block is
μMg
2μMg
zero
Mg
The correct Answer is:C
To solve the problem, we need to analyze the situation of the block in the lift that is accelerating downwards with an acceleration equal to g.
1. Understanding the System:
- The lift is moving downwards with an acceleration a=g.
- A block of mass m is placed on the floor of the lift.
- The coefficient of friction between the block and the lift is μ.
2. Reference Frame:
- We will analyze the block from the reference frame of the lift. In this frame, the block experiences a pseudo force due to the acceleration of the lift.
3. Forces Acting on the Block:
- The gravitational force acting on the block is mg (downwards).
- The pseudo force acting on the block (due to the downward acceleration of the lift) is ma where a=g. Thus, the pseudo force is mg (upwards).
- The normal force N acts upwards on the block from the lift floor.
4. Net Force in the Vertical Direction:
- Since the lift is accelerating downwards with g, the net force in the vertical direction must be zero for the block to remain in equilibrium in the lift's frame.
- Therefore, we can write the equation:
N+mg−mg=0
- Simplifying this gives:
N=0
5. Frictional Force Calculation:
- The frictional force Ff acting on the block is given by the equation:
Ff=μN
- Since we found that N=0, we substitute this into the friction equation:
Ff=μ⋅0=0
6. Conclusion:
- The friction acting on the block is zero because the normal force between the block and the lift is zero.
Final Answer:
The friction acting on the block is 0.
- The lift is moving downwards with an acceleration a=g.
- A block of mass m is placed on the floor of the lift.
- The coefficient of friction between the block and the lift is μ.
- We will analyze the block from the reference frame of the lift. In this frame, the block experiences a pseudo force due to the acceleration of the lift.
- The gravitational force acting on the block is mg (downwards).
- The pseudo force acting on the block (due to the downward acceleration of the lift) is ma where a=g. Thus, the pseudo force is mg (upwards).
- The normal force N acts upwards on the block from the lift floor.
- Since the lift is accelerating downwards with g, the net force in the vertical direction must be zero for the block to remain in equilibrium in the lift's frame.
- Therefore, we can write the equation:
N+mg−mg=0
- Simplifying this gives:
N=0
- The frictional force Ff acting on the block is given by the equation:
Ff=μN
- Since we found that N=0, we substitute this into the friction equation:
Ff=μ⋅0=0
- The friction acting on the block is zero because the normal force between the block and the lift is zero.
The friction acting on the block is 0.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Match the columns
7 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
A block of mass m is kept on a horizontal table. If the static friction coefficient is μ., find the frictional force acting on the block.
View SolutionA lift is moving down with an acceleration equal to the acceleration due to gravity. A body of mass M kept on the floor of the lift is pulled horizontally. If the coefficient of friction is μ then the frictional resistance offered by the body is:
View Solution
Knowledge Check
A block of mass 10kg is placed on a rough horizontal surface having coefficient of friction μ=0.5 . If a horizontal force of 100N is acting on it, then acceleration of the block will be.
A10ms−2B5ms−2C15ms−2D0.5ms−2
A block of mass 10 kg is kept on a fixed rough (μ=0.8) inclined plane of angle of inclination 30∘. The frictional force acting on the block is

View SolutionA lift is moving upwards with an acceleration of 2m/sec2. Inside the lift a 4kg block is kept on the floor. On the top of it , 3kg block is placed and again a 2kg block is kept on the 3kg . Calculator :
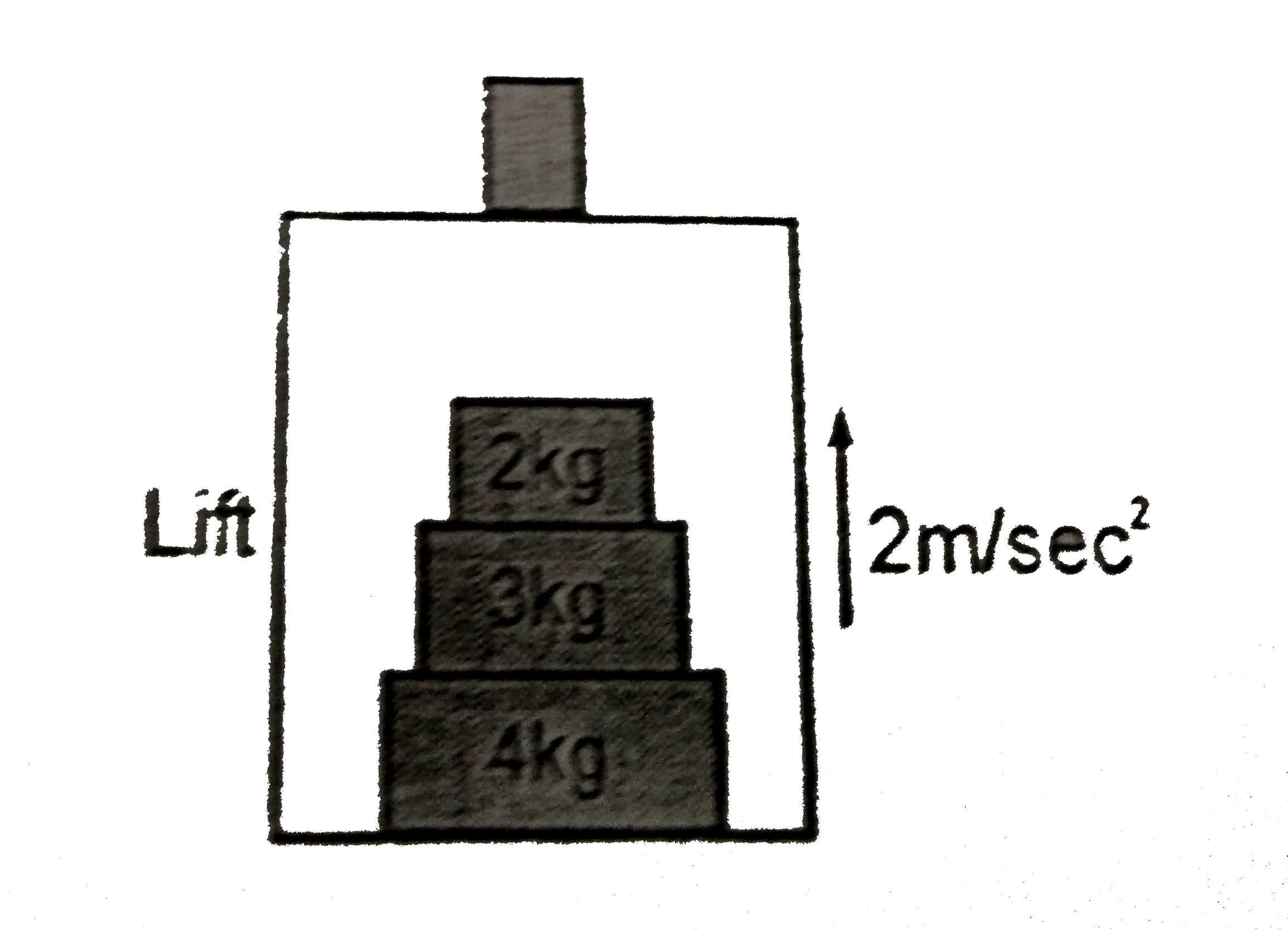
(i) contact force between 2kg block and the 3kg block.
(ii) contact force between 4kg block and floor of the lift.
Draw the free body diagrams properly & take g=10m/sec2
View SolutionA block of mass 'm' is placed on the floor of a lift, moving upward with an uniform acceleration a = g. (μis the coefficient of friction between block and the floor of lift). If a horizontal force of umg acts on the block, then horizontal acceleration of the body is .......
View SolutionA lift moving with a uniform velocity v in which a block of mass m is lying .The friction force offered by the when coefficient of friction is μ=0.5 will be
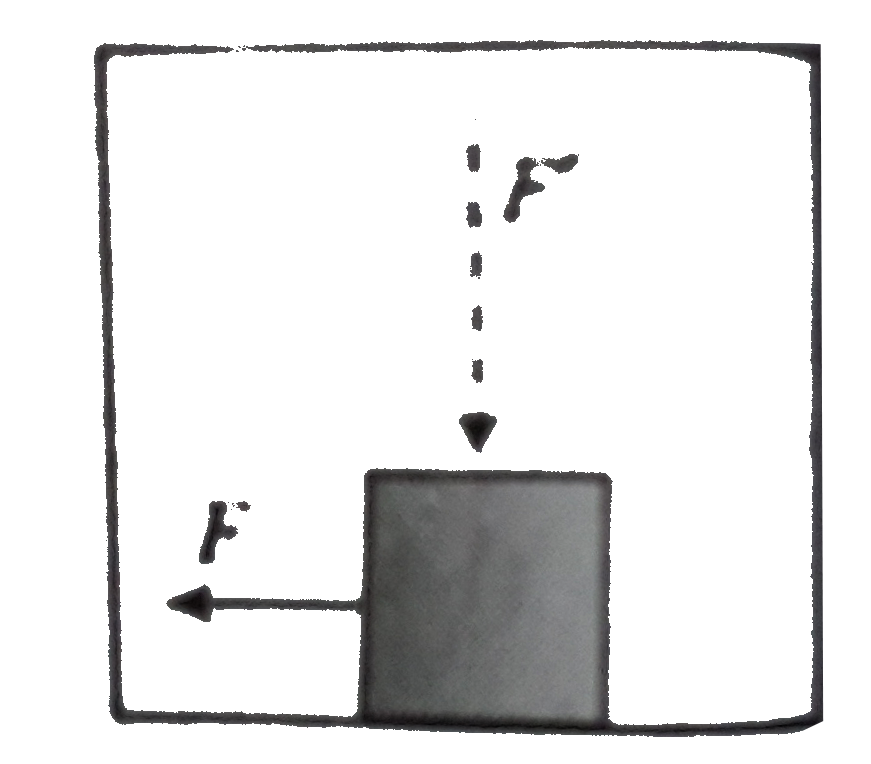
View SolutionA block of mass m is kept on the floor of a freely falling lift .During the free fall of the lift, the block is pulled horizontally with a force of F=5N,μs=0.1The friction force on the block will be
View SolutionA block of mass m is pulled by a force of constant power P placed on a rough horizontal plane. The friction coefficient between the block and the surface is μ. Then
View SolutionA block of mass 10kg is placed on a rough horizontal surface having coefficient of friction μ=0.5 . If a horizontal force of 100N is acting on it, then acceleration of the block will be.
View Solution
