A body of mass m is released from a height h to a scale pan hung from a spring. The spring constant of the spring is k, the mass of the scale pan is negligible and the body does not bounce relative to the pan, then the amplitude of vibration is
mgk√1−2hkmg
mgk
mgk+mgk√1+2hkmg
mgk−mgk√1−2hkmg
The correct Answer is:C
Decreases in potential energy of the mass when the pan gets lowered by distance y (due to mass hitting on the pan) =mg(h+y), where h is the height through which the mass falls on the pan. Increases in elastic potential of the spring =12ky2 (according to low of conservation of energy)
or mg(h+y)=12ky2
or ky2−2mgy−2mgh=0
y=2mg±√4m2g2+8mghk2k
=mgk±mgk√(1+2hkmg)
Velocity of the pan will be maximum at the time of collision and will be zero at the lowet position. Hence y should be the amplitude of oscillation.
So, amplitude of vibration=[mgk+mgk√(1+2hkmg)]
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct
35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Assertion Reasoning
6 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective
21 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
A load of mass m falls from a height h on to the scale pan hung from a spring , as shown in the figure . If the spring constant is k , mass of the not bounce , relative to the pan , then the amplitude of vibration is
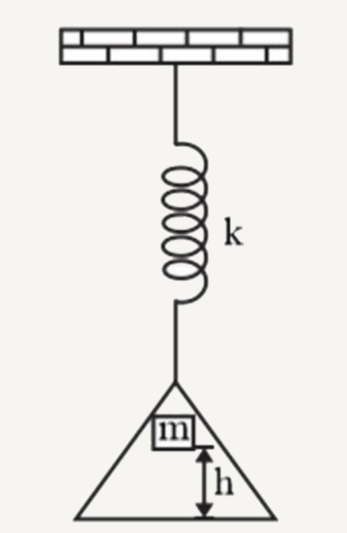
View Solution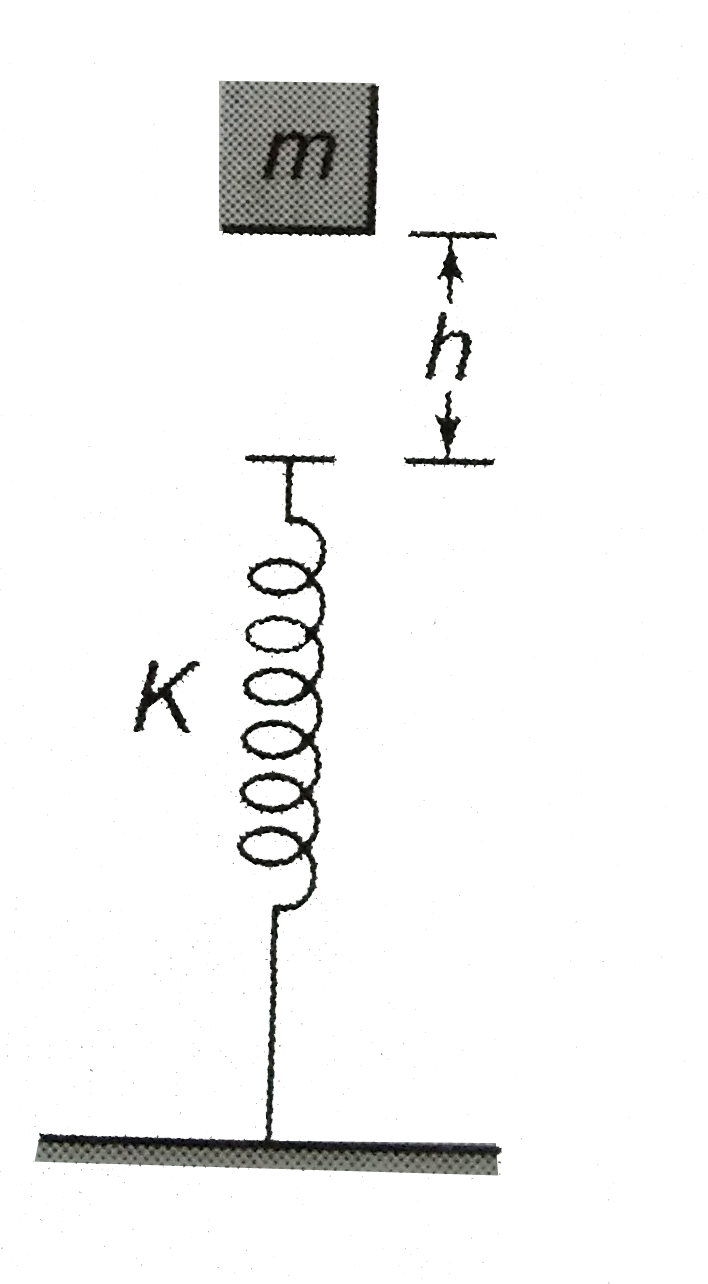
A block is released from height h, find the maximum compression of spring of spring constant k.
View Solution
Knowledge Check
A body of mass m falls from a height h onto the pan of a spring balance. The masses of the pan and spring are negligible. The force constant of the spring is k. The body sticks to the pan and oscillates simple harmonically. The amplitude of oscillation is
 AmgkBmgk√1+2hkmgCmgk+mgk√1+2hkmgDNone of these
AmgkBmgk√1+2hkmgCmgk+mgk√1+2hkmgDNone of theseA load of mass m falls from a height h on to the scale pan hung from a spring , as shown in the figure . If the spring constant is k , mass of the not bounce , relative to the pan , then the amplitude of vibration is
 Amg/dBmgk√(1+2hkmg)Cmgk+mgk√(1+2hkmg)Dmgk√(1+2hkMg−mgk)
Amg/dBmgk√(1+2hkmg)Cmgk+mgk√(1+2hkmg)Dmgk√(1+2hkMg−mgk)A load of mass m falls from a height h on to the scale pan hung from a spring as shown in the adjoining figure. If the spring constant is k and mass of the scale pan is zero and the mass m does not bounce relative to the pan, then the amplitude of vibration is
 AmgkBmgk√(1+2hkmg)Cmgk+mgk√(1+2hkmg)Dmgk√(1+2hkmg−mgk)
AmgkBmgk√(1+2hkmg)Cmgk+mgk√(1+2hkmg)Dmgk√(1+2hkmg−mgk)
A block of mass m is relesed from rest from a height h onto a smooth sledge of mass M fitted with an ideal spring of stiffness k.

View SolutionA body of mass m falls from a height h on to the pan of a spring balance. The masses of the pan and spring are negligible. The spring constant of the spring is k. Having stuck to the pan the body starts performing harmonic oscillations in the vertical direction. Find the amplitude and energy of oscillation.
View SolutionA block of 200 g mass is dropped from a height of 2 m on to a spring and compress the spring to a distance of 50 cm. The force constant of the spring is
View Solution
A block of mass m initially at rest is dropped from a height h on to a spring of force constant k . the maximum compression in the spring is x then
View SolutionA body of mass m falls from a height h onto the pan of a spring balance. The masses of the pan and spring are negligible. The force constant of the spring is k. The body sticks to the pan and oscillates simple harmonically. The amplitude of oscillation is

View Solution
