Frequency of a particle executing SHM is 10 Hz. The particle is suspended from a vertical spring. At the highest point of its oscillation the spring is unstretched. Maximum speed of the particle is (g=10ms)
2πms
πms
1πms
12π/ms
The correct Answer is:D
To find the maximum speed of a particle executing simple harmonic motion (SHM) suspended from a vertical spring, we can follow these steps:
1. Identify Given Values:
- Frequency f=10Hz
- Acceleration due to gravity g=10m/s2
2. Calculate Angular Frequency (ω):
The angular frequency ω is related to the frequency f by the formula:
ω=2πf
Substituting the given frequency:
ω=2π×10=20πrad/s
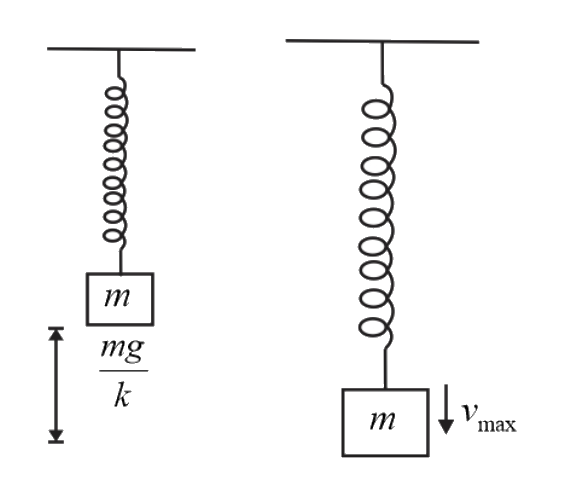
3. Set Up the Equilibrium Condition:
At the equilibrium position, the weight of the particle is balanced by the spring force:
mg=kx
Here, x is the amplitude a of the motion. Thus, we can write:
mg=ka
4. Express Spring Constant (k):
The angular frequency ω is also related to the spring constant k and mass m by:
ω2=km
Rearranging gives:
k=mω2
5. Substitute for k in the Equilibrium Condition:
Substitute k into the equilibrium condition:
mg=mω2a
Cancel m (assuming m≠0):
g=ω2a
6. Solve for Amplitude (a):
Rearranging gives:
a=gω2
Substitute g=10m/s2 and ω=20π:
a=10(20π)2=10400π2=140π2m
7. Calculate Maximum Speed (Vmax):
The maximum speed in SHM is given by:
Vmax=a⋅ω
Substitute the values of a and ω:
Vmax=(140π2)⋅(20π)=20π40π2=12πm/s
Final Answer:
The maximum speed of the particle is:
Vmax=12πm/s
- Frequency f=10Hz
- Acceleration due to gravity g=10m/s2
The angular frequency ω is related to the frequency f by the formula:
ω=2πf
Substituting the given frequency:
ω=2π×10=20πrad/s
At the equilibrium position, the weight of the particle is balanced by the spring force:
mg=kx
Here, x is the amplitude a of the motion. Thus, we can write:
mg=ka
The angular frequency ω is also related to the spring constant k and mass m by:
ω2=km
Rearranging gives:
k=mω2
Substitute k into the equilibrium condition:
mg=mω2a
Cancel m (assuming m≠0):
g=ω2a
Rearranging gives:
a=gω2
Substitute g=10m/s2 and ω=20π:
a=10(20π)2=10400π2=140π2m
The maximum speed in SHM is given by:
Vmax=a⋅ω
Substitute the values of a and ω:
Vmax=(140π2)⋅(20π)=20π40π2=12πm/s
The maximum speed of the particle is:
Vmax=12πm/s
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct
35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Assertion Reasoning
6 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective
21 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
Frequency of a particle executing SHM is 10Hz. The particle is suspended form a vertical spring. At the highest point of its oscillation the spring is unstretched. Find the maximum speed of the particle: (g=10m/s2)
View SolutionA particle suspended from a vetical spring oscillastes 10 times per sencon. At the highest point of oscillation the spring becomes unstretched. A. Find the maximum speed of the block. B. Find the speed when the spring is stretche by 0.20 cm. Take g=π2ms−2
View Solution
Knowledge Check
A particle suspended from a vertical spring oscillates 8 times per second. At the highest point of oscillation the spring becomes unstretched. The maximum speed of the block will be
A10 cm/sB20 cm/sC30 cm/sD40 cm/sThe acceleration of a particle executing S.H.M. is
AAlways directed towards the equilibrium positionBAlways towards the one endCContinuously changing in directionDMaximum at the mean positionA mass is suspended from a vertica spring which is executing SHM of frequency 5 Hz.
The spring is unstretched at the highest point of oscillation. Maximum speed of the mass is (take, acceleration due to gravity, g=10m/s2 )A2πm/sBπm/sC12πm/sD1πm/s
A particle suspended from a vertical spring oscillates 10 times per second. At the highest point of oscillation , the spring becomes upstretched . Find the speed when the spring is stretched by 0.20 cm . (Take , g=π2m/s2)
View SolutionDisplacement of a particle executing SHM s x=10(cosπt+sinπt). Its maximum speed is
View SolutionThe displacement of a particle executing SHM is given by y=0.5 sint cm . The maximum speed of the particle is
View SolutionA particle at the end of a spring executes S.H,M with a period t2 If the period of oscillation with two spring in .
View SolutionA particle executing S.H.M. has a maximum speed of 30cm/s and a maximum acceleration of 60cm/s2. The period of oscillation is
View Solution
