A body of mass m was suspended by a non-stretched spring, and then set fre without push. The stiffness of the spring is x. Neglecting the mass of the spring , find :
(a) the law of motion y(t), whee y is displacement of the body from the equilibrium position,
(b) the maximum and minimum tensions of the spring in the process of motion.
Let y(t)= displacement of the body from the end of the unstretched position of the spring (not the equilibrium position). Then
m..y=−ky+mg
This equation has the soloution of the form
y=A+Bcos(ωt+α)
if −mω2Bcos(ωt+α)=−k[A+Bcos(ωt+α)]+mg
Then ω2=km and A=mgk
we have y=0 and y=0 at t=0. So
−ωBsinα=0
A+Bcosα=0
Since B>0 and A>0 we have α=π
B=A=mgk
and y=mgk(1−cosωt)
(b) Tension in the spring is
T=ky=mg(1−cosωt)
so Tmax=2mg,Tmin=0
Topper's Solved these Questions
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electric Oscillations
56 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Elastic Waves
39 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Exercise
2 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics
49 Videos
Similar Questions
A body of mass m is suspended from a spring fixed to the ceiling of an elevator car. The stiffness of the spring is x. At the moment t=0 the car starts going up with an accelerationw. Neglecting the mass of the spring , find the law of motion y(t0 of the body relative to the elevator car if y(0)−0 and y(0)=0. Consider the following two cases :
(a) w=const,
(b) w=αt, where αis a constant.
View SolutionA block of mass m strikes a light pan fitted with a vertical spring after falling through a distance h. If the stiffness of the spring is k, find the maximum compression of the spring.
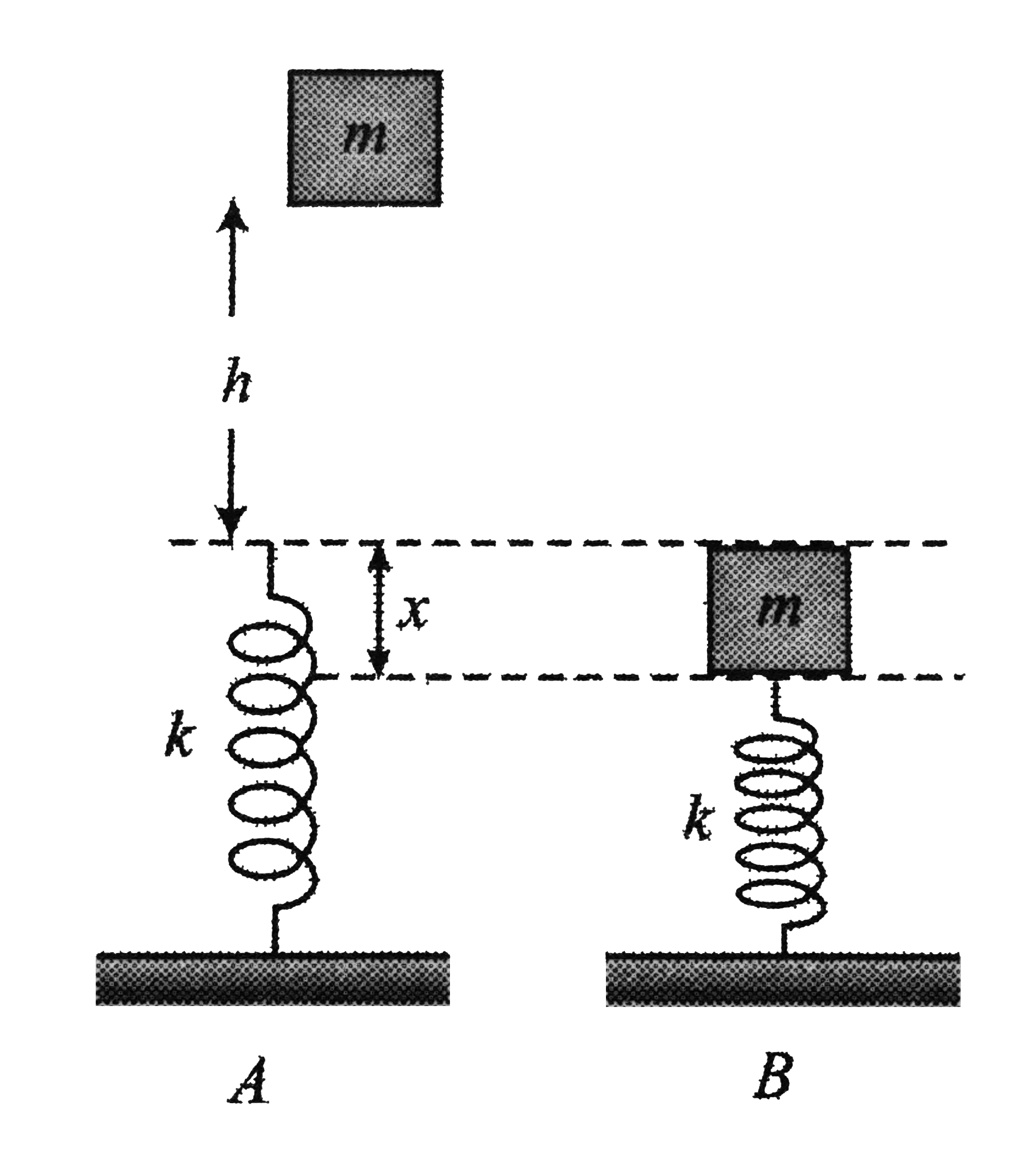
View Solution
Knowledge Check
A body of mass 8kg is suspended through two light springs X and Y connected in series as shown in figure the readings in X and Y respectively are
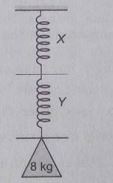 Azero.8kgB6kg,2kgC2kg,6kgD8kg,8kg
Azero.8kgB6kg,2kgC2kg,6kgD8kg,8kgA body of mass 8kg is suspended through two light springs X and Y connected in series as shown in figure the readings in X and Y respectively are
 Azero.8kgB6kg,2kgC2kg,6kgD8kg,8kg
Azero.8kgB6kg,2kgC2kg,6kgD8kg,8kgA body of mass 8 kg is suspended through two light springs X and Y connected in series as shown in figure. The readings is X and Y respectively are :
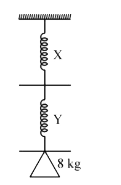 A8 kg, zeroBzero, 8 kgC6 kg, 2 kgD8 kg, 8 kg
A8 kg, zeroBzero, 8 kgC6 kg, 2 kgD8 kg, 8 kg
A block of mass m suspended from a spring of spring constant k. Find the amplitude of S.H.M.
View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionA body of mass m is suspended from a massless spring of natural length l. It stretches the spring through a vertical distance y. The potential energy of the stretched spring is
View SolutionA body of mass m is suspended from three springs as shown in figure. If mass m is displaced slightly then time period of oscillation is

View SolutionA body of mass m is suspended from vertical spring and is set into simple harmonic oscillations of time period T. Next the spring is fixed at one end on a smooth horizontal table and same body is attached at the other end. The body is pulled slightly and then released to produce horizontal oscillations of the spring. The time period of horizontal oscillations is
View Solution
