A body of mass M1 collides elastically with another mass M2 at rest. There is maximum transfer of energy when :
M1>M2
M1<M2
M1=M2
same for all values of M1 and M2
The correct Answer is:C
To solve the problem of maximum energy transfer during an elastic collision between two bodies of masses M1 and M2, we can analyze the situation step by step.
Step 1: Understand Elastic Collision
In an elastic collision, both momentum and kinetic energy are conserved. This means that the total momentum before the collision is equal to the total momentum after the collision, and the total kinetic energy before the collision is equal to the total kinetic energy after the collision.
Step 2: Set Up the Problem
Let:
- Mass M1 be moving with an initial velocity v.
- Mass M2 be at rest (initial velocity = 0).
Step 3: Apply Conservation of Momentum
The conservation of momentum before and after the collision can be expressed as:
M1v+M2⋅0=M1v′1+M2v′2
where v′1 and v′2 are the velocities of M1 and M2 after the collision.
Step 4: Apply Conservation of Kinetic Energy
The conservation of kinetic energy can be expressed as:
12M1v2+0=12M1(v′1)2+12M2(v′2)2
Step 5: Analyze Maximum Energy Transfer
For maximum energy transfer from M1 to M2, we want the velocity of M2 after the collision to be as high as possible. The maximum transfer of energy occurs when the entire kinetic energy of M1 is transferred to M2. This happens when the masses are equal:
M1=M2
Conclusion
Thus, the condition for maximum transfer of energy during an elastic collision is when the masses are equal:
M1=M2
Final Answer
The correct option is that maximum transfer of energy occurs when M1 is equal to M2.
---
In an elastic collision, both momentum and kinetic energy are conserved. This means that the total momentum before the collision is equal to the total momentum after the collision, and the total kinetic energy before the collision is equal to the total kinetic energy after the collision.
Let:
- Mass M1 be moving with an initial velocity v.
- Mass M2 be at rest (initial velocity = 0).
The conservation of momentum before and after the collision can be expressed as:
M1v+M2⋅0=M1v′1+M2v′2
where v′1 and v′2 are the velocities of M1 and M2 after the collision.
The conservation of kinetic energy can be expressed as:
12M1v2+0=12M1(v′1)2+12M2(v′2)2
For maximum energy transfer from M1 to M2, we want the velocity of M2 after the collision to be as high as possible. The maximum transfer of energy occurs when the entire kinetic energy of M1 is transferred to M2. This happens when the masses are equal:
M1=M2
Thus, the condition for maximum transfer of energy during an elastic collision is when the masses are equal:
M1=M2
The correct option is that maximum transfer of energy occurs when M1 is equal to M2.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Taking it together73videos
CENTRE OF MASS
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion and reason21videos
CENTRE OF MASS
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery27videos
CENTRE OF MASS
- BOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery38videos
CALORIMETRY AND HEAT TRANSFER
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions15videos
CENTRE OF MASS, IMPULSE AND MOMENTUM
Similar Questions
A body of mass m1 collides elastically with another body of mass m2 at rest. If the velocity of m1 after collision is 23 times its initial velocity, the ratio of their masses is :
View SolutionA body of mass m1 collides elastically with a stationary body of mass m2 and returns along the same line with one fourth of its initial speed, then m1/m2=
View Solution
Knowledge Check
- Question 1 - Select One
A spherical ball of mass m1 collides head on with another ball of mass m2 at rest . The collision is elastic . The fraction of kinetic energy lost by m1 is :
A4m1m2(m1+m2)2Bm1m1+m2Cm2m1+m2Dm1m2(m1+m2)2
A body of mass m kg collides elastically with another body at rest and then continues to move in the original direction with one half of its original speed. What is the mass of the target body ?
View SolutionA body of mass 3kg collides elastically with another body at rest and then continues to move in the original direction with one half of its original speed. What is the mass of the target body?
View SolutionTwo balls of masses m1=100g and m2=300g are suspended from point A by two equal inextensible threads, each of length l=3235m. Ball of mass m1 is drawn aside and held at the same level as A but at a distance (√32)l from A, as shown in Fig. When ball m1 is released, it collides elastically with the stationary ball of mass m2.
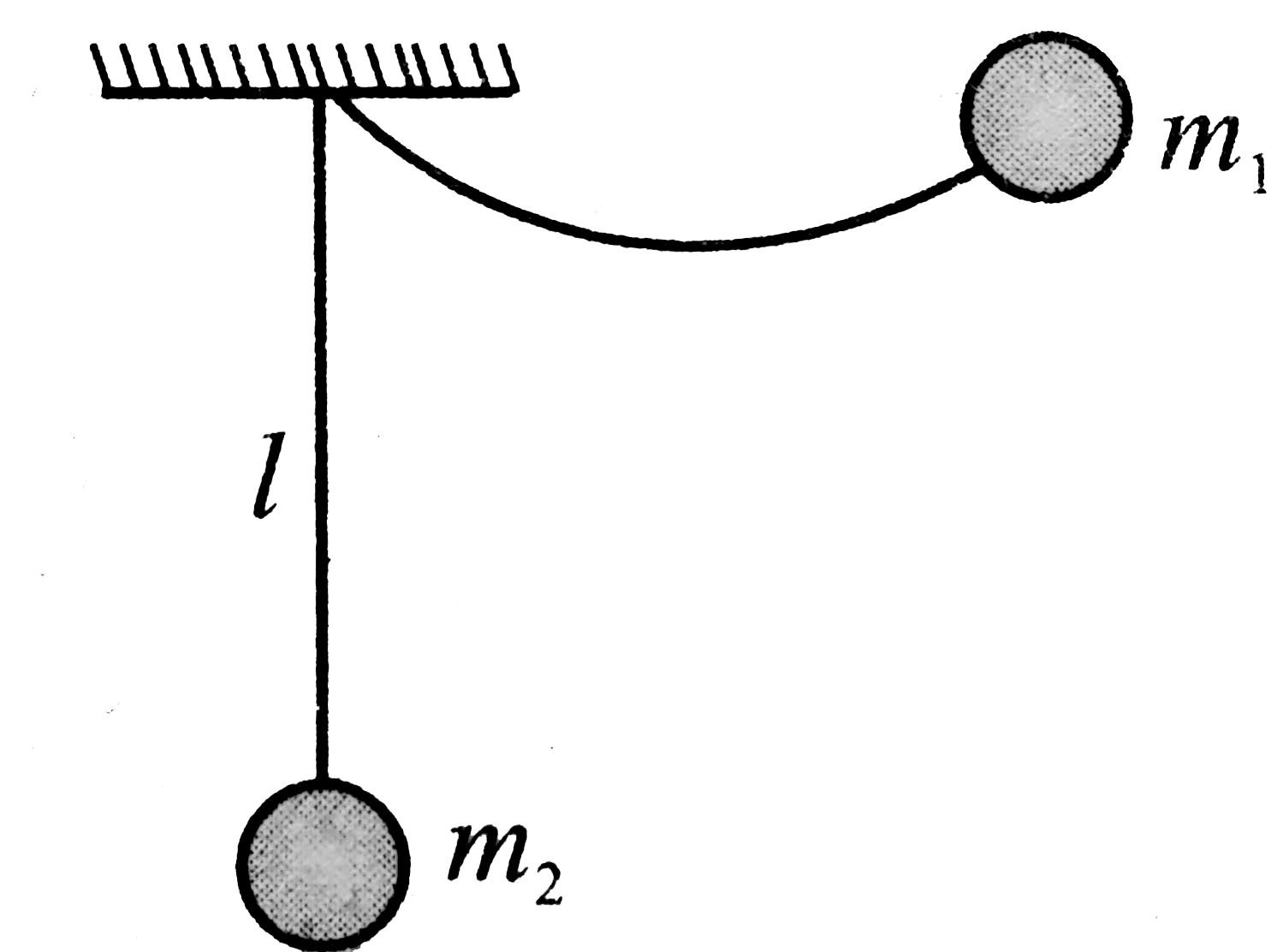 The maximum rise of centre of mass of the ball of mass m2 isView Solution
The maximum rise of centre of mass of the ball of mass m2 isView SolutionA ball of mass M moving with speed v collides perfectly inelastically with another ball of mass m at rest. The magnitude of impulse imparted to the first ball is
View SolutionA ball of mass M moving with speed v collides perfectly inelastically with another ball of mass m at rest. The magnitude of impulse imparted to the first ball is
View SolutionA ball of mass M moving with speed v collides perfectly inelastically with another ball of mass m at rest. The magnitude of impulse imparted to the first ball is
View SolutionAn object of mass M1 moving horizontally with speed u colides elstically with another object of mass M2 at rest. Select correct statement.
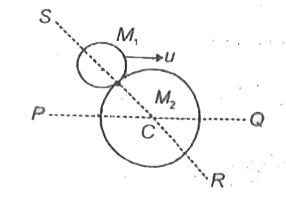 View Solution
View Solution

