A body of mass m1 collides elastically with a stationary body of mass m2 and returns along the same line with one fourth of its initial speed, then m1/m2=
1
2
0.66
0.33
The correct Answer is:C
To solve the problem, we need to analyze the elastic collision between two bodies, where one body is initially stationary. We will use the principles of conservation of momentum and the properties of elastic collisions.
1. Define Initial Conditions:
- Let the mass of the first body be m1 and its initial velocity be v.
- The mass of the second body is m2 and its initial velocity is 0 (since it is stationary).
2. Post-Collision Velocities:
- After the collision, the first body (mass m1) moves in the opposite direction with a velocity of −v4.
- Let the velocity of the second body (mass m2) after the collision be v2.
3. Apply Conservation of Momentum:
- The law of conservation of momentum states that the total momentum before the collision equals the total momentum after the collision.
- Initial momentum:
pinitial=m1⋅v+m2⋅0=m1v
- Final momentum:
pfinal=m1(−v4)+m2v2
- Setting initial momentum equal to final momentum:
m1v=−m1v4+m2v2
4. Rearranging the Equation:
- Rearranging gives:
m1v+m1v4=m2v2
- Simplifying:
54m1v=m2v2
5. Use Elastic Collision Property:
- For elastic collisions, the relative velocity of separation is equal to the relative velocity of approach:
v2−(−v4)=v−0
- This simplifies to:
v2+v4=v
- Rearranging gives:
v2=v−v4=3v4
6. Substituting v2 Back:
- Substitute v2 back into the momentum equation:
54m1v=m2(3v4)
- Cancel v from both sides (assuming v≠0):
54m1=34m2
7. Finding the Ratio m1m2:
- Rearranging gives:
m1m2=35
Final Answer:
m1m2=35
- Let the mass of the first body be m1 and its initial velocity be v.
- The mass of the second body is m2 and its initial velocity is 0 (since it is stationary).
- After the collision, the first body (mass m1) moves in the opposite direction with a velocity of −v4.
- Let the velocity of the second body (mass m2) after the collision be v2.
- The law of conservation of momentum states that the total momentum before the collision equals the total momentum after the collision.
- Initial momentum:
pinitial=m1⋅v+m2⋅0=m1v
- Final momentum:
pfinal=m1(−v4)+m2v2
- Setting initial momentum equal to final momentum:
m1v=−m1v4+m2v2
- Rearranging gives:
m1v+m1v4=m2v2
- Simplifying:
54m1v=m2v2
- For elastic collisions, the relative velocity of separation is equal to the relative velocity of approach:
v2−(−v4)=v−0
- This simplifies to:
v2+v4=v
- Rearranging gives:
v2=v−v4=3v4
- Substitute v2 back into the momentum equation:
54m1v=m2(3v4)
- Cancel v from both sides (assuming v≠0):
54m1=34m2
- Rearranging gives:
m1m2=35
m1m2=35
Similar Questions
A body of mass M1 collides elastically with another mass M2 at rest. There is maximum transfer of energy when :
View SolutionA body of mass m1 collides elastically with another body of mass m2 at rest. If the velocity of m1 after collision is 23 times its initial velocity, the ratio of their masses is :
View Solution
Knowledge Check
A spherical ball of mass m1 collides head on with another ball of mass m2 at rest . The collision is elastic . The fraction of kinetic energy lost by m1 is :
A4m1m2(m1+m2)2Bm1m1+m2Cm2m1+m2Dm1m2(m1+m2)2
A body of mass m kg collides elastically with another body at rest and then continues to move in the original direction with one half of its original speed. What is the mass of the target body ?
View SolutionTwo bodies of masses m1andm2(<m1) are connected to the ends of a massless cord and allowed to move as shown in figure. The pulley is both massless and frictionless. The acceleration of the centre of mass is (m1−m2)n(m1+m2)2g. Find the value of n.

View SolutionA body of mass 1 kg strikes elastically with another body at rest and continues to move in the same direction with one fourth of its initial velocity. The mass of the other bodyis-
View SolutionA particle of mass m1, makes a head on elastic collision with another stationary body of mass m2 If m1, rebounds with half of its original speed then (m1m2) is
View SolutionA body of mass m collides against a wall with the velocity v and rebounds with the same speed. Its magnitude of change of momentum is
View Solution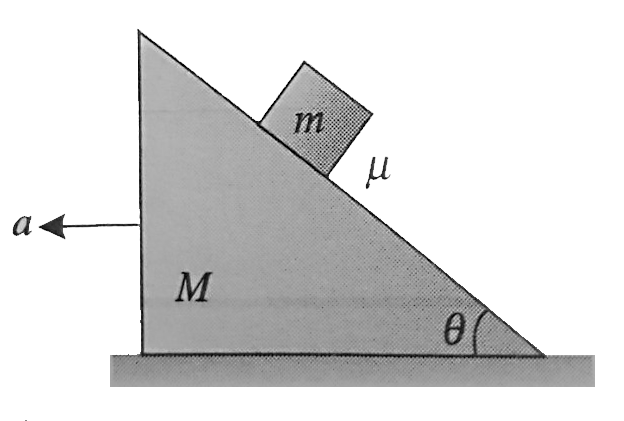
A block of mass m is at rest relative to the stationary wedge of mass M. The coefficient of friction between block and wedge is μ. The wedge is now pulled horizontally with acceleration a as shown in figure. Then the minimum magnitude of a for the friction between block and wedge to be zero is:
View SolutionA particle of mass m1 moves with speed v and collides head on with a stationary particles of mass m2 . The first particle continues to move in the same direction
If m1m2 is (e = coefficient of restitution )
View Solution
