A ball of mass M moving with speed v collides perfectly inelastically with another ball of mass m at rest. The magnitude of impulse imparted to the first ball is
Mv
mv
MmM+mv
M2M+mv
The correct Answer is:C
To solve the problem of finding the magnitude of impulse imparted to the first ball in a perfectly inelastic collision, we can follow these steps:
Step 1: Understand the scenario
We have two balls:
- Ball 1 (mass = M) is moving with speed v.
- Ball 2 (mass = m) is at rest.
Step 2: Apply the conservation of momentum
In a perfectly inelastic collision, the two balls stick together after the collision. Therefore, we can apply the conservation of momentum before and after the collision.
The initial momentum of the system is:
Pinitial=M⋅v+m⋅0=Mv
After the collision, the two balls move together with a common velocity V0. The total mass after the collision is M+m, so the final momentum is:
Pfinal=(M+m)⋅V0
By conservation of momentum:
Pinitial=Pfinal
Mv=(M+m)⋅V0
Step 3: Solve for the final velocity V0
Rearranging the equation gives us:
V0=MvM+m
Step 4: Calculate the impulse
Impulse is defined as the change in momentum. The impulse I imparted to the first ball can be calculated as:
I=Pfinal−Pinitial
The initial momentum of the first ball is:
Pinitial=Mv
The final momentum of the first ball after the collision (which is now part of the combined mass) is:
Pfinal=M⋅V0=M⋅MvM+m=M2vM+m
Now, substituting these into the impulse formula:
I=M2vM+m−Mv
Step 5: Simplify the impulse expression
To simplify:
I=M2vM+m−Mv(M+m)M+m
I=M2v−Mv(M+m)M+m
I=M2v−M2v−MmvM+m
I=−MmvM+m
Since impulse is a magnitude, we take the absolute value:
I=MmvM+m
Final Answer
The magnitude of impulse imparted to the first ball is:
I=MmvM+m
We have two balls:
- Ball 1 (mass = M) is moving with speed v.
- Ball 2 (mass = m) is at rest.
In a perfectly inelastic collision, the two balls stick together after the collision. Therefore, we can apply the conservation of momentum before and after the collision.
Pinitial=M⋅v+m⋅0=Mv
Pfinal=(M+m)⋅V0
Pinitial=Pfinal
Mv=(M+m)⋅V0
Rearranging the equation gives us:
V0=MvM+m
Impulse is defined as the change in momentum. The impulse I imparted to the first ball can be calculated as:
I=Pfinal−Pinitial
Pinitial=Mv
Pfinal=M⋅V0=M⋅MvM+m=M2vM+m
I=M2vM+m−Mv
To simplify:
I=M2vM+m−Mv(M+m)M+m
I=M2v−Mv(M+m)M+m
I=M2v−M2v−MmvM+m
I=−MmvM+m
I=MmvM+m
The magnitude of impulse imparted to the first ball is:
I=MmvM+m
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-B (SUBJECTIVE TYPE QUESTIONS) (ONE OPTIONS IS CORRECT)
45 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-C (OBJECTIVE TYPE QUESTIONS) (MORE THAN ONE OPTIONS ARE CORRECT)
16 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - TRY YOURSELF
95 Videos
- WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
12 Videos
Similar Questions
A particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 3 m at rest. Loss of KE of system in the collision is
View SolutionA particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 2m at rest. Find loss of kinetic energy of system in the collision.
View SolutionA particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 2m at rest. Find loss of kinetic energy of system in the collision.
View SolutionA small ball of mass m moving with speed v collides elastically with a simple pendulum with bob of mass m at rest. The maximum height attained by the bob after collision is
View SolutionAn object of mass m1 moving with speed v collides with another object of mass m2 at rest and stick to it. Find the impulse imparted to the second object.
View SolutionA ball of mass m moving with speed u collides with a smooth horizontal surface at angle θ with it as shown in figure. The magnitude of impulse imparted to surface by ball is [Coefficient of restitution of collision is e]

View SolutionA ball of mass m moving at a speed v collides with another ball of mass 3m at rest. The lighter block comes to rest after collisoin. The coefficient of restitution is
View SolutionA ball of mass m moving with velocity v collides head-on which the second ball of mass m at rest. I the coefficient of restitution is e and velocity of first ball after collision is v1 and velocity of second ball after collision is v2 then
View SolutionA ball of mass 4 kg moving on a smooth horizontal surface makes an elastic collision with another ball of mass m at rest in the line of motion of first ball. If after collision first ball moves in the same direction with one fourth of its velocity before collision, then mass of second ball is
View SolutionA spherical ball of mass M moving with initial velocity V collides elastically with another ball of mass M, which is fixed at one end of L shaped rigid massless frame as shown in Fig. (a). The L shaped frame contains another mass M connected at the other end.
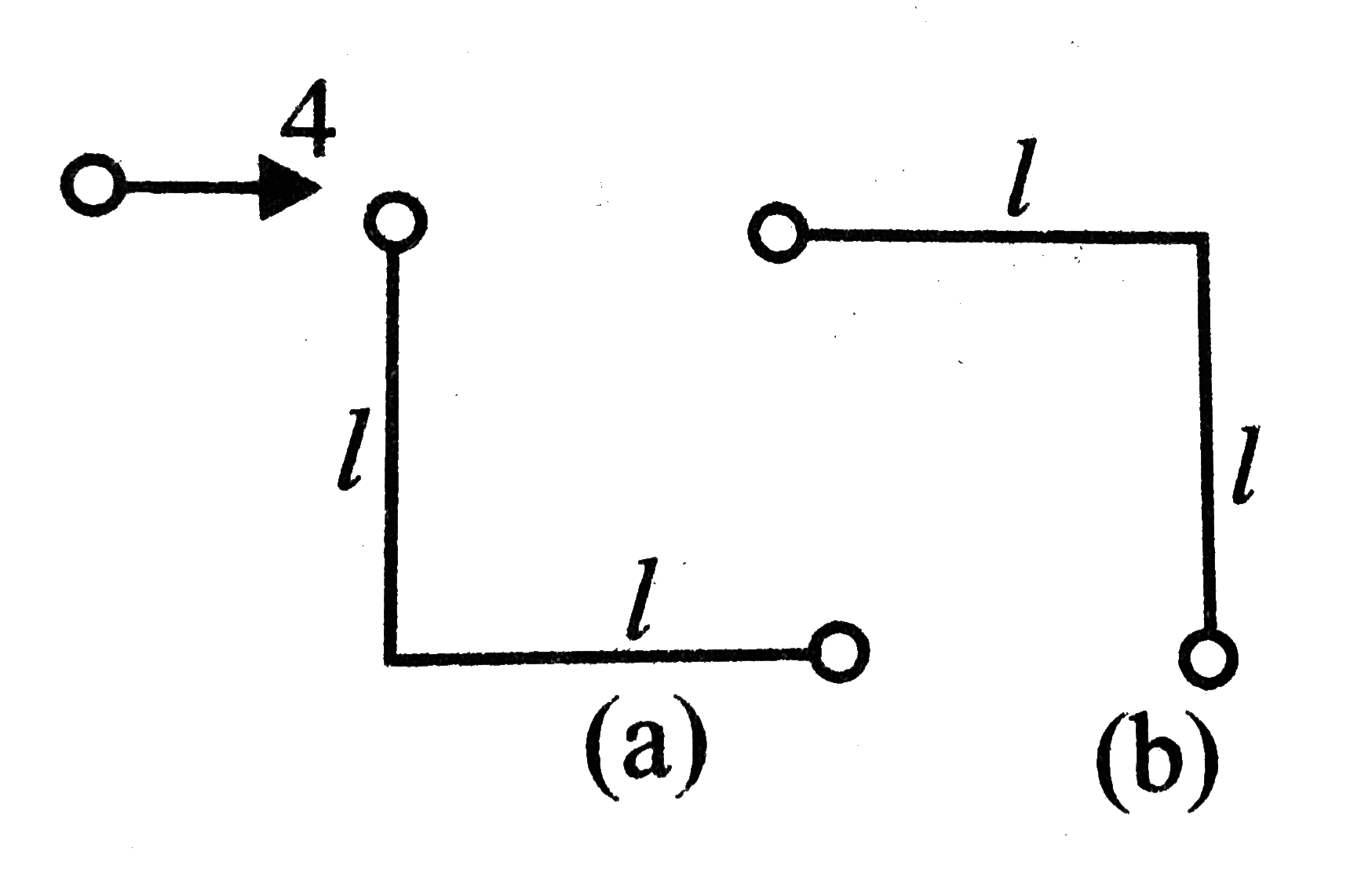
The speed of the striking mass after collision is
View Solution
