A capacitor having capacity of is charged to and then the plates of the capacitor are connected to a resistance wire. The heat produced in joule will be
The correct Answer is:B
To solve the problem of calculating the heat produced when a capacitor is discharged through a resistance, we can follow these steps:
1. Identify the given values:
- Capacitance (C) = 2 µF = 2×10−6 F
- Voltage (V) = 200 V
2. Use the formula for energy stored in a capacitor:
The energy (U) stored in a capacitor can be calculated using the formula:
U=12CV2
3. Substitute the values into the formula:
U=12×(2×10−6)×(200)2
4. Calculate V2:
V2=2002=40000
5. Plug V2 back into the energy formula:
U=12×(2×10−6)×40000
6. Simplify the expression:
U=(1×10−6)×40000=4×10−2 joules
7. Conclusion:
The heat produced when the capacitor is discharged through the resistance is 4×10−2 joules.
Final Answer:
The heat produced in joules is 0.04 joules or 4×10−2 joules.
---
- Capacitance (C) = 2 µF = 2×10−6 F
- Voltage (V) = 200 V
The energy (U) stored in a capacitor can be calculated using the formula:
U=12CV2
U=12×(2×10−6)×(200)2
V2=2002=40000
U=12×(2×10−6)×40000
U=(1×10−6)×40000=4×10−2 joules
The heat produced when the capacitor is discharged through the resistance is 4×10−2 joules.
The heat produced in joules is 0.04 joules or 4×10−2 joules.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (B) Chapter exercises
17 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
If the two plates of the charged capacitor are connected by a wire, then
View SolutionA 2μF capacitor is charged to 100V, and then its plates are connected by a conducting Wire. The heat produced is .
View SolutionA capacitor of capacity 2μF is charged to 100V. What is the heat generated when this capacitor is connected in parallel to an another capacitor of same capacity?
View SolutionTwo capacitors of 2μF and 3μF are charged to 150V and 120V, respectively. The plates of capacitor are connected as shown in the figure. An uncharged capacitor of capacity 1.5μF falls to the free end of the wire. Then
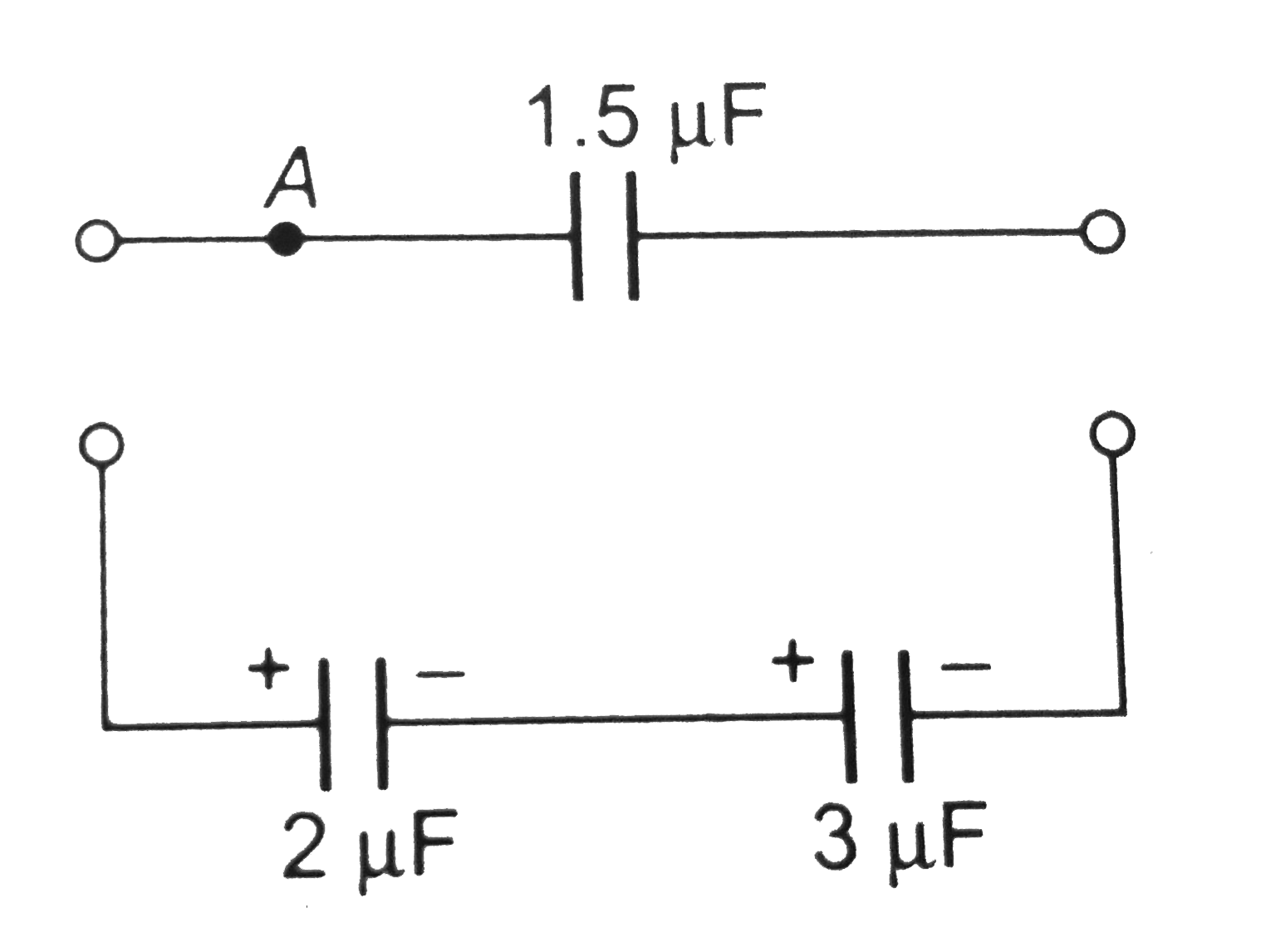
View SolutionTwo capacitors of 2μF and 3μF are charged to 150V and 120V, respectively. The plates of capacitor are connected as shown in the figure. An uncharged capacitor of capacity 1.5μF falls to the free end of the wire. Then

View SolutionA capacitor of capacitance 4μF is charged to 80V and another capacitor of capacitance 6μF is charged to 30V are connected to each other using zero resistance wires such that the positive plate of one capacitor is connected to the positive plate of the other. The energy lost by the 4μF capacitor in the process in X∗10−4J. Find the value of X.
View SolutionA capacitor of capacitance 4μF is charged to 80V and another capacitor of capacitance 6μF is charged to 30V are connected to each other using zero resistance wires such that the positive plate of one capacitor is connected to the positive plate of the other. The energy lost by the 4μF capacitor in the process in X∗10−4J. Find the value of X.
View SolutionA parallel -plate capacitor having plate area 25.0cm^2 and a separation2.00mm between the plates .the capacitor is connected to a bettery of 12.0V.(a)find the charge on the capacitor .(b) the plate separation is decrerased to 1.00mm. Find the extra charge given by the bettery to the positive plate.
View SolutionA capacitor of capacitance 5μF is charged to potential 20V and isolated. Now, an uncharged capacitor is connected in parallel to it. If the charge distributes equally on these capacitors, find total energy stored in capacitors.
View SolutionA capacitor 4μF charged to 50V is connected to another capacitor of 2μF charged to 100V with plates of like charges connected together. The total energy before and after connection in multiples of (10−2J) is
View Solution
