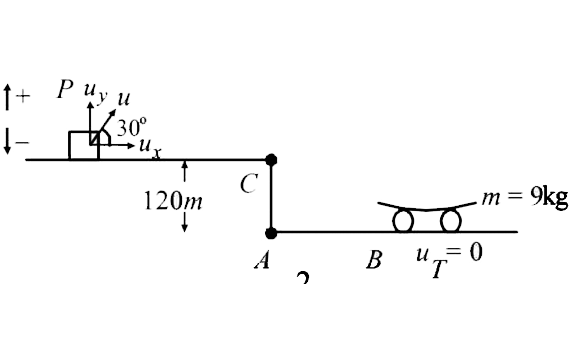
A car P is moving with a uniform speed $5 \sqrt{3} m / s$ towards a carriage of mass 9 kg at rest kept on the rails at a point B as shown in figure. The height AC is 120 m. Cannon balls of 1 kg are fired from the car with an initial velocity $100 m / s$ at an angle $30^{\circ}$ with the horizontal. The first cannon hall hits the stationary carriage after a time $t_{0}$ and sticks to it. Determine $t_{0}$ .

At $t_{0}$ , the second cannon ball is fired. Assume that the resistive force between the rails and the carriage is constant and ignore the vertical motion of the carriage throughout. If the second ball also hits and sticks to the carriage, what will be the horizontal velocity of the carriage just after the second impact?

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, B

Consider the vetical motion of the cannon ball
$u_{y} = + 100 {sin 30}^{\circ}$
$s_{y} = - 120 m$
$a_{y} = - 10 m / s^{2}$
$t = t_{0}$
$s = u t + \frac{1}{2} a t^{2} ∴ - 120 = 50 t_{0} - 5 t_{0}^{2}$
$\Rightarrow t_{0}^{2} - 10 t_{0} - 24 = 0$
$∴ t_{0} = \frac{(- 10) \pm \sqrt{100} - 4 (1) (- 24)}{2} = 12 or - 2$ [Not valid]
$∴ t_{0} = 12 sec .$

The horizontal velocity of the cannon ball remains the same
$∴ u_{x} = 100 {cos 30}^{\circ} = 50 \sqrt{3} m s^{- 1}$
$∴$ Applying conservation of linear momentum to the
cannon ball-trolley system in horizontal direction. If m is the mass of cannon ball and M is the mass of the trolley then,
$μ_{x} + M \times 0 = (m + M) v_{x}$
$∴ v_{x} = \frac{m u_{x}}{m + M}$ where $v_{x}$ is the velocity of the
cannon ball-trolley system.
$∴ v_{x} = \frac{1 \times 50 \sqrt{3}}{1 + 9} = 5 \sqrt{3} m / s$
The second ball also struck the trolley,
Therefore, in time 12 seconds, the trolley covers a distance
of $60 \sqrt{3} m .$
For trolley after 12 seconds,
$u = 5 \sqrt{3} m / s, v = ?, t = 12 s$

$s = 60 \sqrt{3} m, s = u t + \frac{1}{2} a t^{2}$
$\Rightarrow 60 \sqrt{3} = 5 \sqrt{3} \times 12 + \frac{1}{2} \times a \times 144$
$∴ a = 0 m / s^{2} ∴ v = u + a t = 5 \sqrt{3} m / s .$
To find the final velocity of the carriage after the second
impact we again apply conservation of linear momentum in
the horizontal direction
$μ_{x} + (M + m) v_{x} = (M + 2 m) v_{f}$
$∴ 1 \times 50 \sqrt{3} + (9 + 1) 5 \sqrt{3} = (9 + 2) v_{f}$
$\Rightarrow v_{f} = 15.75 m / s$

|

Updated on:21/07/2023

Class 11 PHYSICS CENTRE OF MASS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A canon of mass 150 kg shot a cannon ball of 1.5 kg which goes with a velocity of 60 m/s. the cannon will recoil with a speed of
A10.5 m/s
B6 m/s
C0.6 m/s
DNone of these
Question 2 - Select One
A shell is fired from a cannon with a velocity $20 m / s$ at an angle $60^{\circ}$ with the horizontal. At the highest point it explodes into three pieces of equal masses . One of the pieces retraces its path to the cannon , the second piece moves vertically up with speed $40 m / s$ , the third piece will move with velocity (immediately after the explosion)
A $20 m / s$ in a horizontal direction
B $40 m / s$ at an angle $45^{\circ}$ with horizontal in an upward direction
C $40 \sqrt{2} m / s$ at an angle $45^{\circ}$ with horizontal in an upward direction
D $40 \sqrt{2} m / s$ at an angle $45^{\circ}$ with horizontal in the downward direction
Question 3 - Select One
A shell is fired from a cannon with a velocity $v (m / s)$ at an angle $θ$ with the horizontal direction. At the highest point in its path it explodes into two pieces of equal mass. on, of the pieces retraces its path to the cannon and the speed, (in $m / s$ ) of the other piece immediately after the explosion is
A $3 v cos θ$
B $2 v cos θ$
C $\frac{3}{2} v cos θ$
D $\sqrt{\frac{3}{2}} v cos θ$

SUNIL BATRA (41 YEARS IITJEE PHYSICS)-MOMENTUM & IMPULSE-JEE Main And Advanced

Home
Ask Doubt
Profile