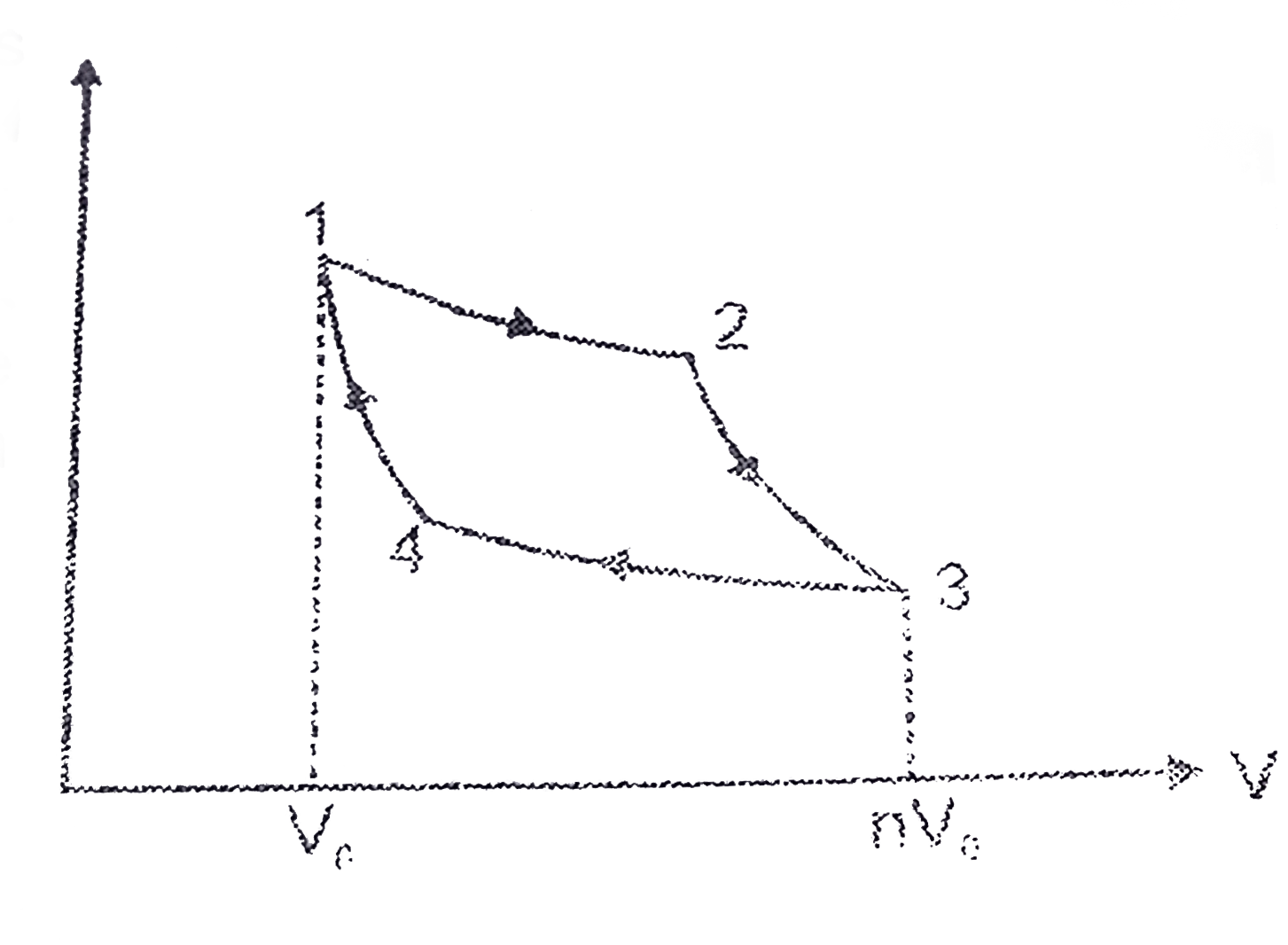
A Carnot engine cycle is shown in the Fig. (2). The cycle runs between temperatures TH=αTL=T0(α>T). Minimum and maximum volume at state 1 and states 3 are V0 and nV0 respectively. The cycle uses one mole of an ideal gas with CP/CV=γ. Here CP and CV are the specific heats at constant pressure and volume respectively. You must express all answers in terms of the given parameters {α,n,T0,V0?} and universal gas constant R.
(a) Find P,V,T for all the states
(b) Calculate the work done by the engine in each process: W12,W23,W34,W41.
(c) Calculate Q, the heat absorbed in the cycle.
P1=RαT0V0,P2=αγγ−1RT0nV0
P3=RT0nV0,P4=RT0α1γ−1V0
V1=V0,V2=nV0α1γ−1
V3=nV0,V4=α1γ−1V0
T1=αT0,T2=αT0
T3=T0,T4=T0
(b) W12=−Rγ−1(T0−αT0)
W34=RT0⎛⎜⎝α1γ−1n⎞⎟⎠
W41=−Rγ−1(αT0−T0)
(c ) Q=RT0(α−1)ln⎛⎝nα(1γ−1)⎞⎠
Topper's Solved these Questions
- KTG & THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - KTG & THERMODYNAMICSEXERCISE - Advancel Level Problems
1 Video
- KINETIC THEORY OF GASES AND THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - KINETIC THEORY OF GASES AND THERMODYNAMICSEXERCISE - Exercise
64 Videos
- MAGNETIC FIELD AND FORCESBOOK - RESONANCE ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Exercise
64 Videos
Similar Questions
Knowledge Check
If CpandCv denoted the specific heats of unit mass of nitrogen at constant pressure and volume respectively, then
ACp=Cv=R28BCp−Cv=R7CCp−Cv=R14DCp−Cv=R
If CPandCV denote the specific heats of nitrogen per unit mass at constant pressure and constant volume respectively, then
View SolutionFor an ideal gas Cp,mCv,m=γ. The molecular mass of the gas is M, its specific heat capacity at constant volume is :
View SolutionCvandCp denote the molar specific heat capacities of a gas at constant volume and constant pressure, respectively. Then
View SolutionCvandCp denote the molar specific heat capacities of a gas at constant volume and constant pressure, respectively. Then
View SolutionCvandCp denote the molar specific heat capacities of a gas at constant volume and constant pressure, respectively. Then
View SolutionCvandCp denote the molar specific heat capacities of a gas at constant volume and constant pressure, respectively. Then
View SolutionCP and CV are specific heats at constant pressure and constant volume respectively. it is observed thatCP−CV=p for helium gas and CP−CV=q for Oxygen gas. The correct relation between p and q is
View Solution
