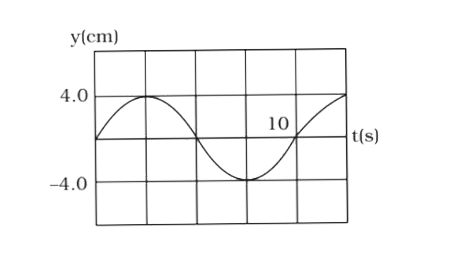
A certain transverse sinusoidal wave of wavelength 20 cm is moving in the positive x direction. The transverse velocity of the particle at x=0 as a function of time is shown. The amplitude of the motion is:

5πcm
π2cm
10πcm
2πcm
The correct Answer is:c
Vmax=Aω=5⇒A2π4=5
⇒A=10πcm
Topper's Solved these Questions
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Single Correct Answer
1 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Multiple Correct
25 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Subjective
16 Videos
- TRANSMISSION OF HEATBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRANSMISSION OF HEATEXERCISE - Single correct
9 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
A transverse sinusoidal wave of wavelength 20 cm is moving along a string towards increasing x. the transverse displacement of the string particle at x=0 as a function of time is shown in figure.

Q. The velocity of propagation of the wave is ?
View SolutionA transverse sinusoidal wave of wavelength 20 cm is moving along a string towards increasing x. The transverse displacement of the string particle at as a function of time is shown in Figure.
The equation of the wave with all the constants evaluated is:
View SolutionFigure shows the position of a particle moving on the x - axis as a function of time
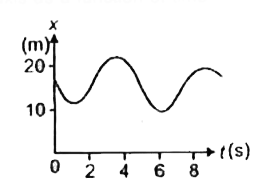
View SolutionFigure shows the position of a particle moving on the X-axis as a function of time.

View SolutionA transverse sinusoidal wave moves along a string in the positive x-direction at a speed of 10cm/s. The wavelength of the wave is 0.5 m and its amplitude is 10cm. At a particular time t,the snapshot of the wave is shown in figure. The velocity of point P when its displacement is 5 cm is

(a) √3π50ˆjm/s
(b)−√3π50ˆjm/s
(c)√3π50ˆim/s
(d) −√3π50ˆim/s
View SolutionA transverse wave of amplitude 2 m, wavelength 4 m and frequency 6 Hz is propagating in a string toward positive y-direction. The equation of the wave may be (y is in m and t is in s)
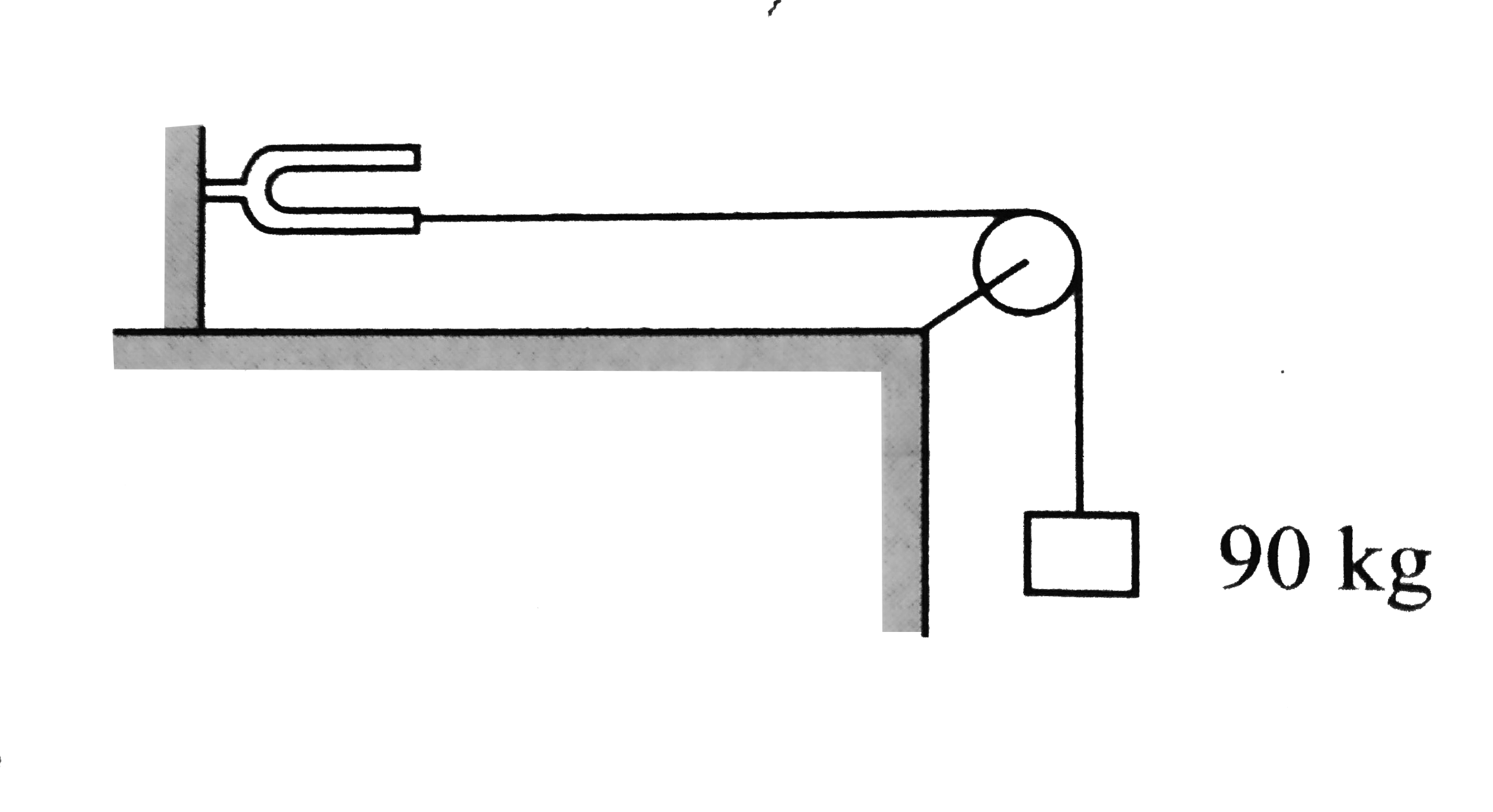
View SolutionOne end of a long string of linear mass density 10−2kgm−1 is connected to an electrically driven tuning fork of frequency 150 Hz. The other end passes over a pulley and is tied to a pan containig a mass of 90 kg. the pulley end absorbs all the incoming energy so that reflected waves from this end have neglidible amplitude , At t =0, the left end (fork end ) of the string is at x=0 has a transverse displacement of 2.5 cm and is moving along positive y-direction. the amplitude of the wave is 5 cm. write down the transverse displacement y (in cetimetres) as function of x(in metres) and t (in seconds ) that describes the wave on the string.
View SolutionThe velocity of a particle moving in the positive direction of x-axis veries as v=10√x. Assuming that at t=0, particle was at x=0
View SolutionA transverse sinusoidal wave is generated at one end of a long horizontal string by a bar that moves the end up and down through a distance by 2.0cm. the motion of bar is continuous and is repeated regularly 125 times per second. If klthe distance between adjacent wave crests is observed to be 15.6cm and the wave is moving along positive x−direction, and at t=0 the element of the string at x=0 is at mean position y=0 and is moving downward, the equation of the wave is best described by
View SolutionOne end of a long string of linear mass dnesity 8.0×10−3kgm−1 is connected to an electrically driven tuning fork of frequency 256 Hz. The other end passes over a pulley and is tied to a pan containing a mass of 90 kg. The pulley end absorbs all the incoming energy so that reflected waves at this end have negligible amplitude. At t=0 the left end (fork end) of the string x=0 has zero transverse displacement (y=0) and is moving along positive y-direction. The amplitude of the wave is 5.0 cm. Write down the transverse displacement y as function of x and t that describest the wave on the string.
View Solution
