A change q=1 C is at (3m,4m) and moving towards positive x-axis with constant velocity of 4 m/s. A long current carrying wire is at origin. Current in this wire is 2.A and towards positive z-axis. Magnetic force on the charge at given instant is
(1.64×107ˆK)N
−(1.92×10−7ˆK)N
(4.8ˆJ−3.2ˆK)×10−7N
(1.6ˆJ−4.8ˆK)×10−7N
The correct Answer is:b
To solve the problem, we need to calculate the magnetic force acting on a charge moving in the vicinity of a long current-carrying wire. Here’s how we can approach the solution step by step:
Step 1: Identify the Given Values
- Charge q=1C
- Position of the charge (x,y)=(3m,4m)
- Velocity of the charge v=4m/s (moving towards positive x-axis)
- Current in the wire I=2A (flowing in the positive z-direction)
Step 2: Calculate the Distance from the Wire
The distance R from the wire (located at the origin) to the charge can be calculated using the Pythagorean theorem:
R=√x2+y2=√32+42=√9+16=√25=5m
Step 3: Calculate the Magnetic Field B due to the Wire
The magnetic field B around a long straight current-carrying wire is given by the formula:
B=μ0I2πR
Where μ0 (the permeability of free space) is approximately 4π×10−7T m/A.
Substituting the values:
B=(4π×10−7)×22π×5=8×10−710=8×10−8T
The direction of the magnetic field due to the right-hand rule is out of the plane (positive z-direction).
Step 4: Determine the Direction of the Velocity and Magnetic Field
- Velocity →v is along the positive x-axis: →v=4^i
- Magnetic field →B is in the positive z-direction: →B=8×10−8^k
Step 5: Calculate the Magnetic Force →F
The magnetic force on a charge moving in a magnetic field is given by:
→F=q(→v×→B)
Calculating the cross product:
→v×→B=(4^i)×(8×10−8^k)=4×8×10−8(^i×^k)=32×10−8(−^j)=−32×10−8^j
Thus, the force becomes:
→F=1×(−32×10−8^j)=−32×10−8^jN
Step 6: Final Result
The magnetic force on the charge at the given instant is:
→F=−3.2×10−7^jN
This indicates that the force is acting in the negative y-direction.
- Charge q=1C
- Position of the charge (x,y)=(3m,4m)
- Velocity of the charge v=4m/s (moving towards positive x-axis)
- Current in the wire I=2A (flowing in the positive z-direction)
The distance R from the wire (located at the origin) to the charge can be calculated using the Pythagorean theorem:
R=√x2+y2=√32+42=√9+16=√25=5m
The magnetic field B around a long straight current-carrying wire is given by the formula:
B=μ0I2πR
Where μ0 (the permeability of free space) is approximately 4π×10−7T m/A.
B=(4π×10−7)×22π×5=8×10−710=8×10−8T
The direction of the magnetic field due to the right-hand rule is out of the plane (positive z-direction).
- Velocity →v is along the positive x-axis: →v=4^i
- Magnetic field →B is in the positive z-direction: →B=8×10−8^k
The magnetic force on a charge moving in a magnetic field is given by:
→F=q(→v×→B)
Calculating the cross product:
→v×→B=(4^i)×(8×10−8^k)=4×8×10−8(^i×^k)=32×10−8(−^j)=−32×10−8^j
Thus, the force becomes:
→F=1×(−32×10−8^j)=−32×10−8^jN
The magnetic force on the charge at the given instant is:
→F=−3.2×10−7^jN
This indicates that the force is acting in the negative y-direction.
Topper's Solved these Questions
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - More than One Option is Correct
25 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Comprehension type Questions
16 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Integer type Questions
10 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
- MEASUREMENT AND ERRORSBOOK - DC PANDEY ENGLISHCHAPTER - MEASUREMENT AND ERRORSEXERCISE - Subjective
19 Videos
Similar Questions
A block of mass 1kg is at x=10m and moving towards negative x−aξs with velocity 6m/s. Another block of mass 2kg is at x=12m and moving towards positive x−axis with velocity 4m/s at the same instant. Find position of their centre of mass after 2s.
View SolutionAt time t=0, a particle is at (2m,4m). It starts moving towards positive x-axis with constant acceleration 2m/s2 (initial velocity=0). After 2 s, an additional acceleration of 4m/s2 starts acting on the particle in negative y-direction also. Find after next 2 s.
(a) velocity and
(b) coordinates of particle.
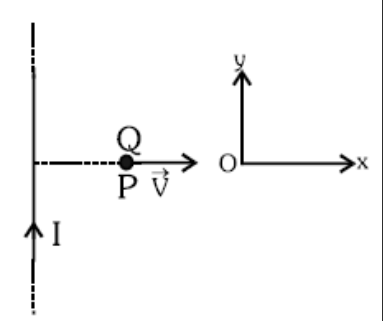
View SolutionA very long straight wire carries a current I. At the instant when a charge +Q at point P has velocity→V, as shown, the force on the charge is-
View SolutionA charged is moving with constant velocity parallel to a horizontal current carrying long wire. The direction of velocity of that particle and the current are same. If the force acting on the particle are only magnetic force due to wire and gravitational force due to earth, then the particle :
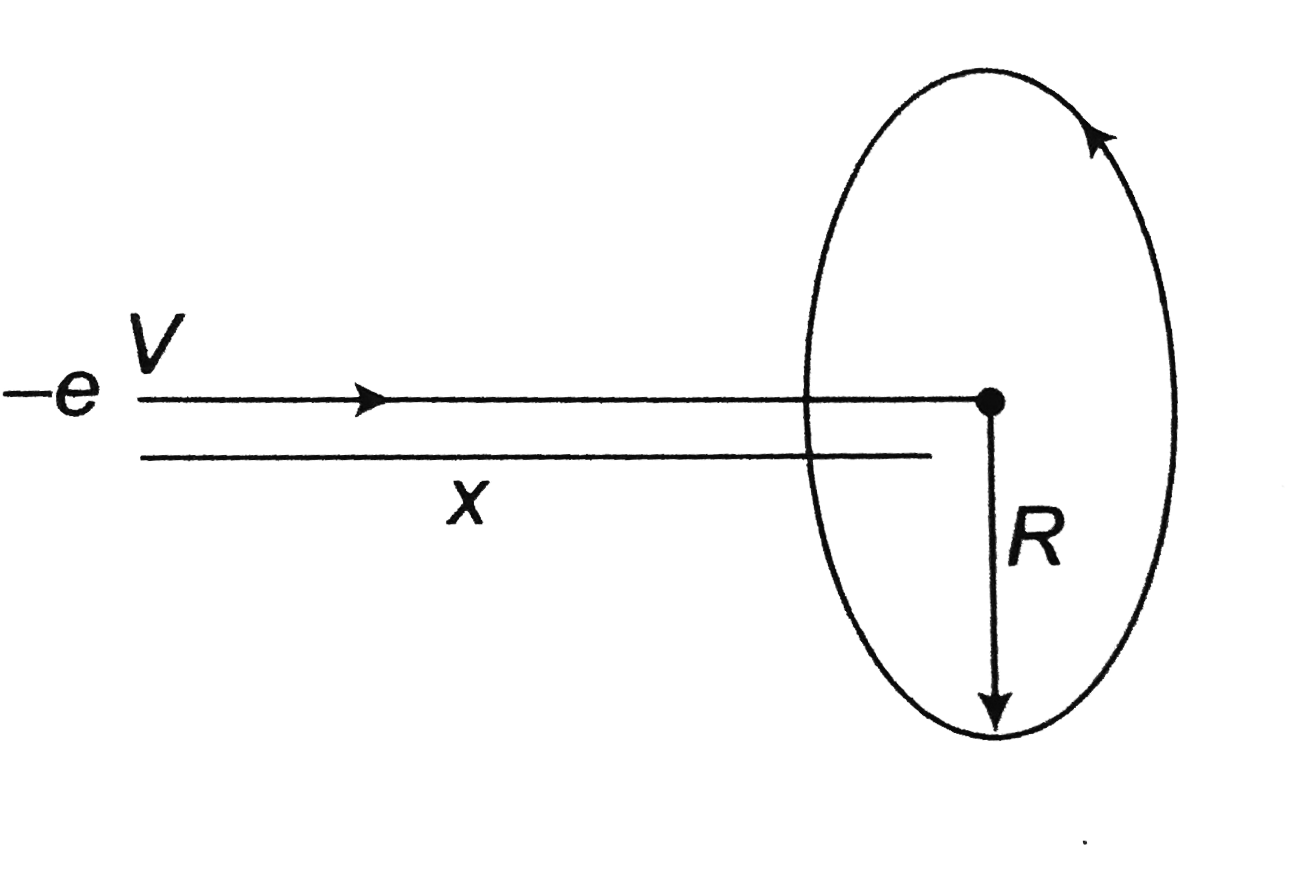
View SolutionAn electron moving with a velocity v along the positive x-axis approaches a circular current carrying loop as shown in the fig. the magnitude of magnetic force on electron at this instant is
View Solutiona very long straight wire carries a current I. at the instant when are charge -Q at point P has velocity v as shown in figure the force on the charge is

View SolutionA very long straight wire carries a current I. At the instant when a charge +Q at point P has velocity →V, as shown, the force on the charge is
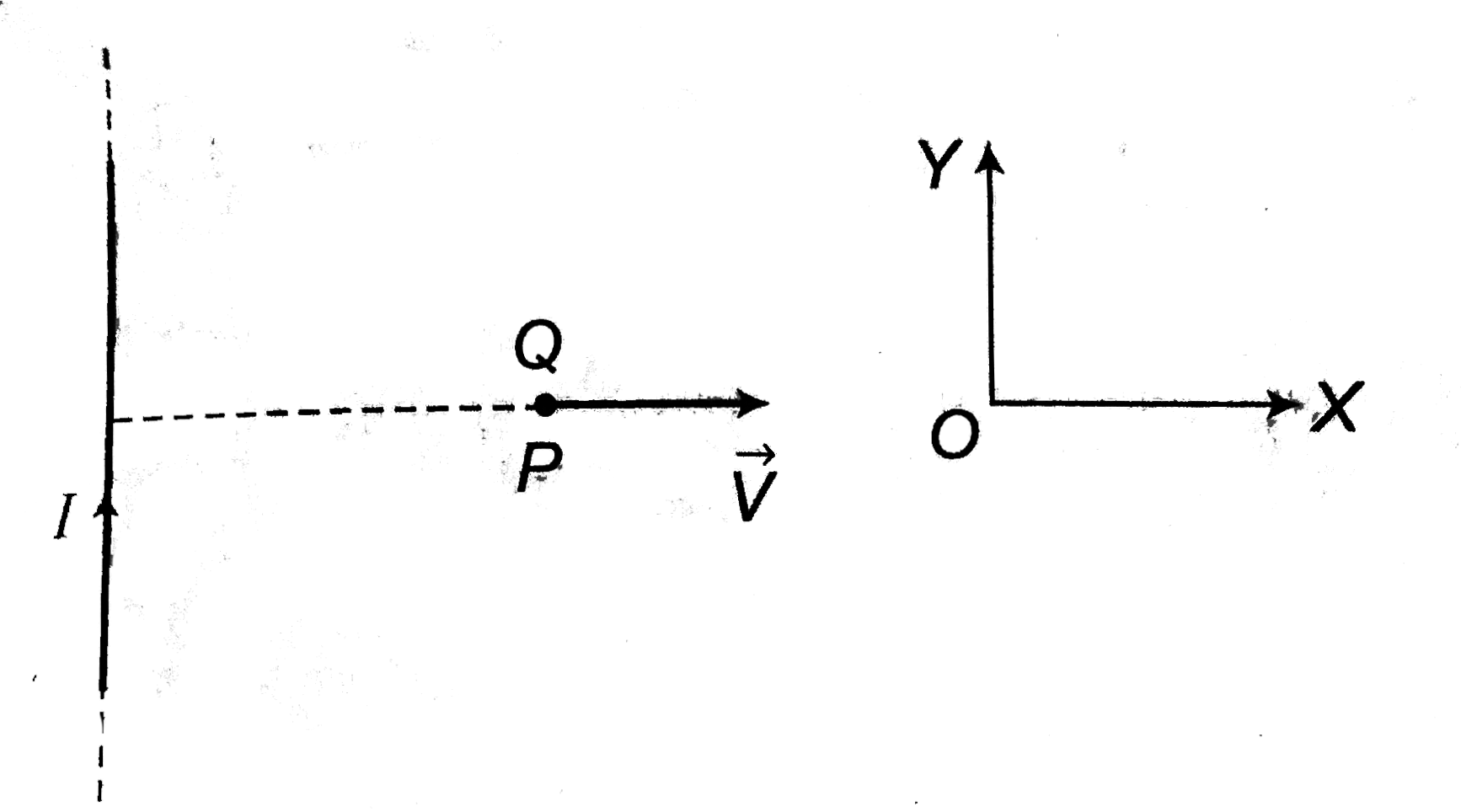
View SolutionA current of 10A is established in a long wire along the positive z-axis. Find the magnetic field (vec B) at the point (1m , 0 , 0).
View SolutionA long, straight wire carries a current along the z-axis. One can find two points in the x-y plane such that
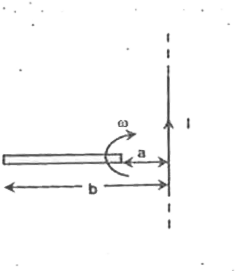
View SolutionA copper rod moves with a constant angular velocity ω about a long straight wire carrying a current I. If the ends of the rod from the wire are at distances a and b, then the e.m.f induced in the rod is
View Solution
