A charge is distributed uniformly over a ring of radius ‘a’. Obtain an expression for the electric intensity E at a point on the axis of the ring. Hence show that for points at large distances from the ring, it behaves like a point charge.

Video Solution

Text Solution

Verified by Experts

Let us consider a circular loop of radius a held perpendicular to the plane of paper.
Let whole of loop carries a charge q. charge on a small element of loop MN of length dl is
$d q = \frac{q}{2 π a} d l$ . . . (i)

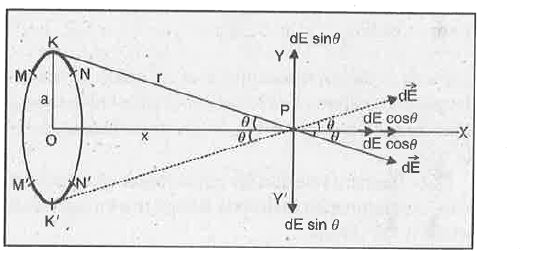
Electric field at P due to charge element MN is
$d E = \frac{1}{4 π ε_{0}} \frac{d q}{r^{2}}$
$= \frac{1}{4 π ε_{0}} \frac{d q}{(x^{2} + a^{2})}$ along PX
dE can be resolved into two rectangular components. dE cos $θ$ acting horizontally along PZ and $d E sin θ$ acting along PY.
For a pair diagrammatically opposite element M., N., dE cos $θ$ acts along PX and hence addd up but $d E sin θ$ along PY. cancel with dE sin $θ$ along PY.
$∴ \sum d E sin θ = 0$ for full loop and dE cos $θ$ addd up
$∴ E = \sum d E cos θ$
$= \sum \frac{1}{4 π ε_{0}} \frac{d q}{(x^{2} + a^{2})} \times \frac{x}{{(x^{2} + a^{2})}^{1 / 2}}$
or $E = \int \frac{1}{4 π ε_{0}} \times \frac{x}{{(x^{2} + a^{2})}^{3 / 2}} \times \frac{q}{2 π a} d l$ [Substituting the value of dq from (i)]
or $E = \frac{1}{4 π ε_{0}} \times \frac{x}{{(x^{2} + a^{2})}^{3 / 2}} \times \frac{q}{2 π a} \int d l$
But $\int d l = l = 2 π a$
$∴ E = \frac{1}{4 π ε_{0}} \times \frac{x}{{(x^{1} + a^{2})}^{3 / 2}} \times \frac{q}{2 π a} \times 2 π a$
or $E = \frac{q x}{4 π ε_{0} {(x^{2} + a^{2})}^{3 / 2}}$ . . (ii)
Special case. when $x > > a$ i.e., P lies far off, then $a^{2} < < x^{2}$ and hence can be neglected.
$∴ E = \frac{q x}{4 π ε_{0} {(x^{2})}^{3 / 2}} = \frac{q x}{4 π ε_{0} x^{3}}$
or $E = \frac{1}{4 π ε_{0}} \times \frac{q}{x^{2}}$
which is the expression for E at a distance x from a charge q. therefore circular loop of charge behaves as a point when P is at a very very large distance from the loop.

Updated on:21/07/2023