A charge q is unifromly distributed over the volume of a unifrom ball of mass m and radius R which rotates with an angular velocity ω about the axis passing through its centre. Find the respective magnetic moment and its ratio to the mechanical moment.
The magentic moment must clearly be along the axis of rotation. Consider a volume element dV. It contains a charge q4π/3R3dV. The rotation of the sphere causes this charge to resolve around the axis and constiude a current.
3q4πRdV×ω2π
Its magentic moment will be
3q4πR3dV×ω2π×πr2sin2θ
So that total magnetic moment is
pm=∫R0∫π03q2R3r2sinθdθ×ωr2sin2θ2dr=3q2R3×ω2×R55×43=15qR2ω
The mechanical moment is
M=25mR2ω, So, pmM=q2m
Topper's Solved these Questions
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electromagnetic Induction
84 Videos
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Motion Of Charged Particle In Magnetic Field
36 Videos
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electric Current
72 Videos
- ELECTRICITY AND MAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRICITY AND MAGNETISMEXERCISE - All Questions
6 Videos
- ELECTROMAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTROMAGNETISMEXERCISE - All Questions
24 Videos
Similar Questions
A disc of mass m, radius r and carrying charge q, is rotating with angular speed ω about an axis passing through its centre and perpendicular to its plane. Calculate its magnetic moment
View SolutionA charge q is uniformly distributed on a non-conducting disc of radius R. It is rotated with an angular speed co about an axis passing through the centre of mass of the disc and perpendicular to its plane. Find the magnetic moment of the disc.
View Solution
Knowledge Check
A copper ball of mass m=1kg with a radius of r=10cm rotates with angular velocity ω=2rad/s about an axis passing through its centre. The work should be performed to increase the angular velocity of rotation of the ball two fold is.
A1.2×10−2JB2.4×10−2JC3.6×10−2JD4.8×10−2JA horizontal disk is rotating with angular velocity ω about a vertical axis passing through its centre. A ball is placed at the centre of groove and pushed slightly. The velocity of the ball when it comes out of the groove -
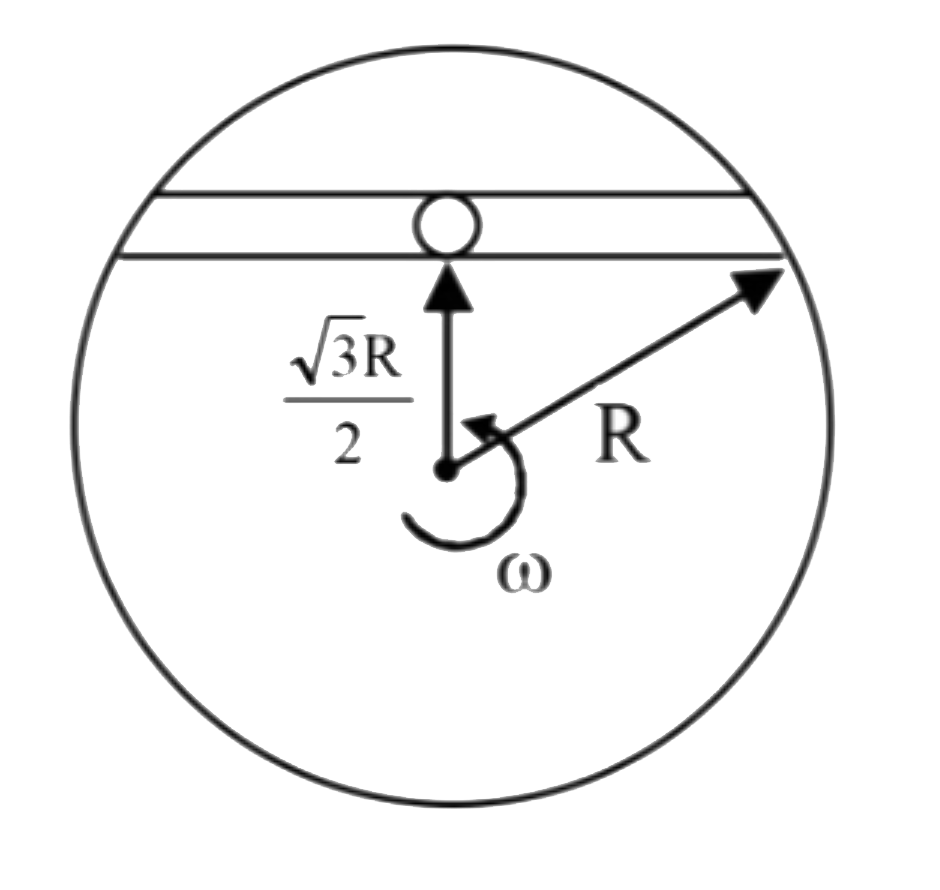 A√32ωRBωR2CωRDωR√2
A√32ωRBωR2CωRDωR√2A charge q is spread uniformly over an insulated loop of radius r. If it is rotated with an angular velocity ω with respect to normal axis then the magnetic moment of the loop is
A12qωr2B43qωr2C32qωr2Dqωr2
A ring of mass m and radius R is being rotated about its axis with angular velocity ω. If a increases then tension in ring
View SolutionA ring of mass m and radius R is being rotated about its axis with constant angular velocity ω in the gravity free space. Find tension in the ring.
View SolutionA charge Q is spread uniformly over an insulated ring of radius R.What is the magnetic moment of the ring if it is rotated with an angluar velocity ω about its axis?
View SolutionA conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.

View SolutionA charge q is spread uniformly over an insulated loop of radius r. If it is rotated with an angular velocity ω with respect to normal axis then the magnetic moment of the loop is :
View Solution
