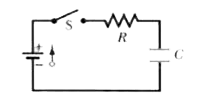
A charged capacitor of capacitance C is discharging through a resistor of resistance R. At what time the charge on the capacitor is equal to one half of its initial value?
RC2
RCloge2
RC loge2
1RCloge2
The correct Answer is:D
To solve the problem step by step, we will use the formula for the charge on a discharging capacitor and find the time at which the charge is half of its initial value.
Step 1: Understand the formula for discharging capacitor
The charge q(t) on a discharging capacitor at time t is given by the formula:
q(t)=q0e−tRC
where:
- q0 is the initial charge,
- R is the resistance,
- C is the capacitance.
Step 2: Set up the equation for half charge
We want to find the time t when the charge q(t) is half of the initial charge q0. Therefore, we set up the equation:
q(t)=q02
Substituting this into the equation gives:
q02=q0e−tRC
Step 3: Simplify the equation
We can divide both sides of the equation by q0 (assuming q0≠0):
12=e−tRC
Step 4: Take the natural logarithm of both sides
To solve for t, we take the natural logarithm of both sides:
ln(12)=−tRC
Step 5: Solve for t
Now, we can isolate t:
t=−RCln(12)
Step 6: Simplify the logarithm
Using the property of logarithms, we know that:
ln(12)=−ln(2)
Thus, we can rewrite t:
t=RCln(2)
Final Answer
The time at which the charge on the capacitor is equal to one half of its initial value is:
t=RCln(2)
The charge q(t) on a discharging capacitor at time t is given by the formula:
q(t)=q0e−tRC
where:
- q0 is the initial charge,
- R is the resistance,
- C is the capacitance.
We want to find the time t when the charge q(t) is half of the initial charge q0. Therefore, we set up the equation:
q(t)=q02
Substituting this into the equation gives:
q02=q0e−tRC
We can divide both sides of the equation by q0 (assuming q0≠0):
12=e−tRC
To solve for t, we take the natural logarithm of both sides:
ln(12)=−tRC
Now, we can isolate t:
t=−RCln(12)
Using the property of logarithms, we know that:
ln(12)=−ln(2)
Thus, we can rewrite t:
t=RCln(2)
The time at which the charge on the capacitor is equal to one half of its initial value is:
t=RCln(2)
Topper's Solved these Questions
Similar Questions
A charged capacitor of capacitance 40μF is discharged through a 50Ω resistance. Determine the time constant of the circuit.
View SolutionSwitch S in Fig. 27-46 is closed at time t= 0, to begin charging an initially uncharged capacitor of capacitance C=49.0μF through a resistor of resistance R=32.0Ω. At what time is the potential across the capacitor equal to that across the resistor?
View Solution
Knowledge Check
LetC be the capacitance of a capacitor discharging through a resistor R. Suppose t1 is the time taken for the energy stored in the capacitor to reduce to half its initial value and t2 is the time taken for the charge to reduce to one-fourth its initial value. Then the ratio t1/t2 will be
A1B1/2C1/4D2If the charge on a capacitor is doubled, the value of its capacitance will be
Adoubled.Bhalved.Cremain the same.Dnone of these.A capacitor of capacitance C carrying charge Q is connected to a source of emf E. Finally, the charge on capacitor would be
AQBQ+CeCCEDnone of these
A capacitor of capacitance 0.5μF is discharged through a resistance. Find the value of resistance if half the charge on capacitor escapes in one minute.
View SolutionThe average life of a radioactive sample is 100 millisecond. A charged capacitor having capacitance 200 μF is connected across a resistance R. For what value of R, the ratio of charge on capacitor to the activity of the sample remains constant with time or independent of time.
View SolutionA capacitor of capacitance C is given a charge go. At time t=0 it is connected to an uncharged capacitor of equal capacitance through a resistance R. Find the charge on the first capacitor and the second capacitor as a function of time t. Also plot the corresponding q-t graphs.
View SolutionA capacitor of capacitance C charged by battery at V volt and then disconnected. At t = 0, it is connected to an uncharged capacitor of capacitance 2C through a resistance R. The charge on the second capacitor as a function of time is given by q=αCV3(1−e−3tβRC) then fing the value of αβ.
View SolutionA charged capacitor of capacitance C is discharged through a resistance R. A radioactive sample decays with an average-life τ.Find the value of R for which the ratio of the electrostatic field energy stored in the capacitor to the activity of the radioactive sample remains constant in time.
View Solution
