A charged particle carrying charge q=10μC moves with velocity v1=106,s−1 at angle 45∘ with x-axis in the xy plane and experience a force F1=5√2mN along the negative z-axis. When the same particle moves with velocity v2=106ms−1 along the z-axis, it experiences a force F2 in y-direction.
Find the magnetic field →B.
(10−3T)(ˆi+ˆj)
(2×10−3T)ˆi
(10−3T)ˆi
(2×10−3T)(ˆi+ˆj)
The correct Answer is:c
To solve the problem, we need to find the magnetic field →B given the conditions of a charged particle moving in a magnetic field. We will break down the solution step by step.
Step 1: Understand the Given Information
We have a charged particle with:
- Charge q=10μC=10×10−6C=10−5C
- Velocity v1=106m/s at an angle 45∘ with the x-axis in the xy-plane.
- Force F1=5√2mN=5√2×10−3N acting along the negative z-axis.
Step 2: Break Down the Velocity Vector
The velocity vector →v1 can be expressed in terms of its components:
→v1=v1x^i+v1y^j
Where:
v1x=v1cos(45∘)=106⋅1√2^i=106√2^i
v1y=v1sin(45∘)=106⋅1√2^j=106√2^j
Thus,
→v1=106√2^i+106√2^j
Step 3: Write the Magnetic Force Equation
The magnetic force →F1 is given by:
→F1=q→v1×→B
Given that →F1=−5√2×10−3^k.
Step 4: Set Up the Cross Product
Let the magnetic field be:
→B=Bx^i+By^j+Bz^k
Now, we compute the cross product →v1×→B:
→v1×→B=∣∣
∣
∣
∣∣^i^j^k106√2106√20BxByBz∣∣
∣
∣
∣∣
Calculating the determinant:
→v1×→B=(106√2Bz−0)^i−(0−106√2Bx)^j+(106√2By−106√2Bx)^k
This simplifies to:
→v1×→B=106√2Bz^i+106√2Bx^j+(106√2By−106√2Bx)^k
Step 5: Equate Forces
Now substituting in the force equation:
q(106√2Bz^i+106√2Bx^j+(106√2By−106√2Bx)^k)=−5√2×10−3^k
Step 6: Solve for Components
From the ^k component:
q(106√2By−106√2Bx)=−5√2×10−3
Substituting q:
10−5(106√2By−106√2Bx)=−5√2×10−3
This leads to:
101√2(By−Bx)=−5√2
Thus,
By−Bx=−10
(Equation 1)
Step 7: Analyze the Second Condition
When the particle moves with v2=106m/s along the z-axis, the force →F2 acts in the y-direction:
→F2=q→v2×→B
Where →v2=106^k.
Calculating the cross product:
→F2=q(106^k×(Bx^i+By^j+Bz^k))=q(106(By^i−Bx^j))
Setting →F2=F2^j:
10−5⋅106(By^i−Bx^j)=F2^j
From the ^j component:
−10−5⋅106Bx=F2
And from the ^i component:
10−5⋅106By=0⇒By=0
Step 8: Solve for Bx
Substituting By=0 into Equation 1:
0−Bx=−10⇒Bx=10
Step 9: Compile the Results
Thus, we have:
- Bx=10T
- By=0
- Bz=0
The magnetic field vector is:
→B=10^i+0^j+0^k=10^iT
Final Answer
The magnetic field →B is:
→B=10T^i
We have a charged particle with:
- Charge q=10μC=10×10−6C=10−5C
- Velocity v1=106m/s at an angle 45∘ with the x-axis in the xy-plane.
- Force F1=5√2mN=5√2×10−3N acting along the negative z-axis.
The velocity vector →v1 can be expressed in terms of its components:
→v1=v1x^i+v1y^j
Where:
v1x=v1cos(45∘)=106⋅1√2^i=106√2^i
v1y=v1sin(45∘)=106⋅1√2^j=106√2^j
Thus,
→v1=106√2^i+106√2^j
The magnetic force →F1 is given by:
→F1=q→v1×→B
Given that →F1=−5√2×10−3^k.
Let the magnetic field be:
→B=Bx^i+By^j+Bz^k
Now, we compute the cross product →v1×→B:
→v1×→B=∣∣
∣
∣
∣∣^i^j^k106√2106√20BxByBz∣∣
∣
∣
∣∣
→v1×→B=(106√2Bz−0)^i−(0−106√2Bx)^j+(106√2By−106√2Bx)^k
This simplifies to:
→v1×→B=106√2Bz^i+106√2Bx^j+(106√2By−106√2Bx)^k
Now substituting in the force equation:
q(106√2Bz^i+106√2Bx^j+(106√2By−106√2Bx)^k)=−5√2×10−3^k
From the ^k component:
q(106√2By−106√2Bx)=−5√2×10−3
Substituting q:
10−5(106√2By−106√2Bx)=−5√2×10−3
This leads to:
101√2(By−Bx)=−5√2
Thus,
By−Bx=−10
(Equation 1)
When the particle moves with v2=106m/s along the z-axis, the force →F2 acts in the y-direction:
→F2=q→v2×→B
Where →v2=106^k.
→F2=q(106^k×(Bx^i+By^j+Bz^k))=q(106(By^i−Bx^j))
Setting →F2=F2^j:
10−5⋅106(By^i−Bx^j)=F2^j
From the ^j component:
−10−5⋅106Bx=F2
And from the ^i component:
10−5⋅106By=0⇒By=0
Substituting By=0 into Equation 1:
0−Bx=−10⇒Bx=10
Thus, we have:
- Bx=10T
- By=0
- Bz=0
→B=10^i+0^j+0^k=10^iT
The magnetic field →B is:
→B=10T^i
Topper's Solved these Questions
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercises Integer
7 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Archives Fill In The Blank
6 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercises Assertion -reasoning
8 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based
8 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False
3 Videos
Similar Questions
A charged particle carrying charge q=10μC moves with velocity v1=106ms−1 at angle 45∘ with x-axis in the xy plane and experience a force F1=5√2mN along the negative z-axis. When the same particle moves with velocity v2=106ms−1 along the z-axis, it experiences a force F2 in y-direction.
Find the magnitude of the force F2.
View SolutionA charged particle carrying charge q=1μc moves in uniform magnetic with velocity v1=106m/s at angle 45∘ with x-axis in the xy-plane and experiences a force F1=5√2N along the negative z-axis. When te same particle moves with velocity v2=106m/s along the z-axis it experiences a force F2 in y-direction. Find
a. the magnitude and direction of the magnetic field
b. the magnitude of the force F2.
View SolutionA particle of charge −16×10−18 coulomb moving with velocity 10ms−1 along the x− axis , and an electric field of magnitude 104/(m) is along the negative z− axis. If the charged particle continues moving along the x- axis , the magnitude of B is
View SolutionA particle of charge −16×10−18 coo–mb moving with velocity 10ms−1 along the x−aξs, and an electric field of magnitude (104)/(m) is along the negative z−ais. If the charged particle continues moving along the x- axis , the magnitude of B is
View SolutionA charge q is moving with a velocity v1=1ˆi m/s at a point in a magentic field and experiences a force F=q[−ˆj+1ˆk] N. If the charge is moving with a voloctiy v2=ˆj m/s at the same point then it experiences a force F2=q(1ˆi−1ˆk) N. The magnetic induction B at that point is
View SolutionWhen a proton has a velocity v=(2ˆi+3ˆj)×106ms, it experience a force F=−(1.28×10−13ˆk) When its velocity is along the z-axis, it experience a force along the x-axis. What is the magnetic field?
View SolutionWhen as proton has a velocity v=(2ˆi+3ˆj)×106ms, it experience a force F=−(1.28×10−13ˆk) When its velocity is along the z-axis, it experience a force along the x-axis. What is the magnetic field?
View SolutionA charged particle having charge 2q and mass m is projected from origin in X-Y plane with a velocity v inclined at an angle of 45∘ with positive X-axis in a region where a uniform magnetic field B unit exists along +z axis. The coordinates of the centre of the circular path of the particle are
View SolutionThree particles starts from origin at the same time with a velocity 2ms−1 along positive x-axis, the second with a velocity 6ms−1 along negative y-axis, Find the velocity of the third particle along x=y line so that the three particles may always lie in a straight line.
View SolutionA particle moving with speed v0=10√2ms−1 strikes a wall at an angle 45∘ as shown in figure. Find magnitude of change in velocity.
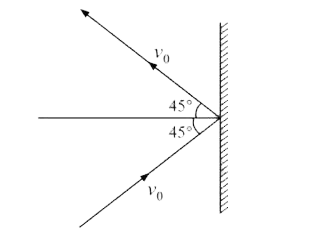
View Solution
