Three particles starts from origin at the same time with a velocity 2ms−1 along positive x-axis, the second with a velocity 6ms−1 along negative y-axis, Find the velocity of the third particle along x=y line so that the three particles may always lie in a straight line.
−3√3
3√2
−3√2
2√2
The correct Answer is:B
To solve the problem, we need to find the velocity of the third particle (C) such that all three particles (A, B, and C) lie on a straight line at all times.
1. Identify the velocities of particles A and B:
- Particle A moves with a velocity of 2m/s along the positive x-axis.
- Particle B moves with a velocity of 6m/s along the negative y-axis.
2. Determine the position of particles A and B after time t:
- The position of particle A after time t is:
Position of A=(2t,0)
- The position of particle B after time t is:
Position of B=(0,−6t)
3. Assume the velocity of particle C:
- Let the velocity of particle C be V along the line x=y. Since it moves at a 45∘ angle, we can express its velocity components as:
Vx=V√2,Vy=V√2
4. Determine the position of particle C after time t:
- The position of particle C after time t is:
Position of C=(Vt√2,Vt√2)
5. Set up the condition for collinearity:
- For particles A, B, and C to be collinear, the slopes of the lines AB and AC must be equal.
- The slope of line AB is given by:
slope of AB=0−(−6t)2t−0=6t2t=3
- The slope of line AC is given by:
slope of AC=Vt√2−0Vt√2−2t=V√2⋅1V√2−2
6. Equate the slopes:
- Set the slopes equal to each other:
3=V/√2(V/√2)−2
7. Cross-multiply and solve for V:
- Cross-multiplying gives:
3(V/√2−2)=V/√2
- Simplifying:
3V/√2−6=V/√2
- Rearranging:
3V/√2−V/√2=6
2V/√2=6
V=6⋅√22=3√2
8. Conclusion:
- The velocity of the third particle C is:
V=3√2m/s
- Particle A moves with a velocity of 2m/s along the positive x-axis.
- Particle B moves with a velocity of 6m/s along the negative y-axis.
- The position of particle A after time t is:
Position of A=(2t,0)
- The position of particle B after time t is:
Position of B=(0,−6t)
- Let the velocity of particle C be V along the line x=y. Since it moves at a 45∘ angle, we can express its velocity components as:
Vx=V√2,Vy=V√2
- The position of particle C after time t is:
Position of C=(Vt√2,Vt√2)
- For particles A, B, and C to be collinear, the slopes of the lines AB and AC must be equal.
- The slope of line AB is given by:
slope of AB=0−(−6t)2t−0=6t2t=3
- The slope of line AC is given by:
slope of AC=Vt√2−0Vt√2−2t=V√2⋅1V√2−2
- Set the slopes equal to each other:
3=V/√2(V/√2)−2
- Cross-multiplying gives:
3(V/√2−2)=V/√2
- Simplifying:
3V/√2−6=V/√2
- Rearranging:
3V/√2−V/√2=6
2V/√2=6
V=6⋅√22=3√2
- The velocity of the third particle C is:
V=3√2m/s
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-III42videos
CENTRE OF MASS
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-IV A32videos
CENTRE OF MASS
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-I40videos
CENTRE OF MASS
- BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON11videos
BASIC MATHEMATICS USED IN PHYSICS &VECTORS
- BOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)3videos
ELASTICITY, SURFACE TENSION AND FLUID MECHANICS
Similar Questions
Three particles start from the origin at the same time, one with a velocity v1 along the x-axis, second along the y-axis with a velocity v2 and third particle moves along the line x = y. The velocity of third particle, so that three may always lie on the same line is:
View SolutionA particle starts from the origin at time t = 0 and moves along the positive x-axis. The graph of velocity with respect to time is shown in figure. What is the position of the particle at time t = 5s ?
 View Solution
View SolutionA body starts from the origin with an acceleration of 6ms−2 along the x - axis and 8ms−2 along the y - axis. Find its distance from the origin after 4s.
View SolutionA particle projected from origin moves in x-y plane with a velocity →v=3ˆi+6xˆj, where ˆi and ˆj are the unit vectors along x and y axis. Find the equation of path followed by the particle :-
View SolutionA time varying force, F=2t is acting on a particle of mass 2kg moving along x-axis. velocity of the particle is 4m/s along negative x-axis at time t=0. Find the velocity of the particle at the end of 4s.
View SolutionThe variation of velocity of a particle moving along a straight line is shown in . is
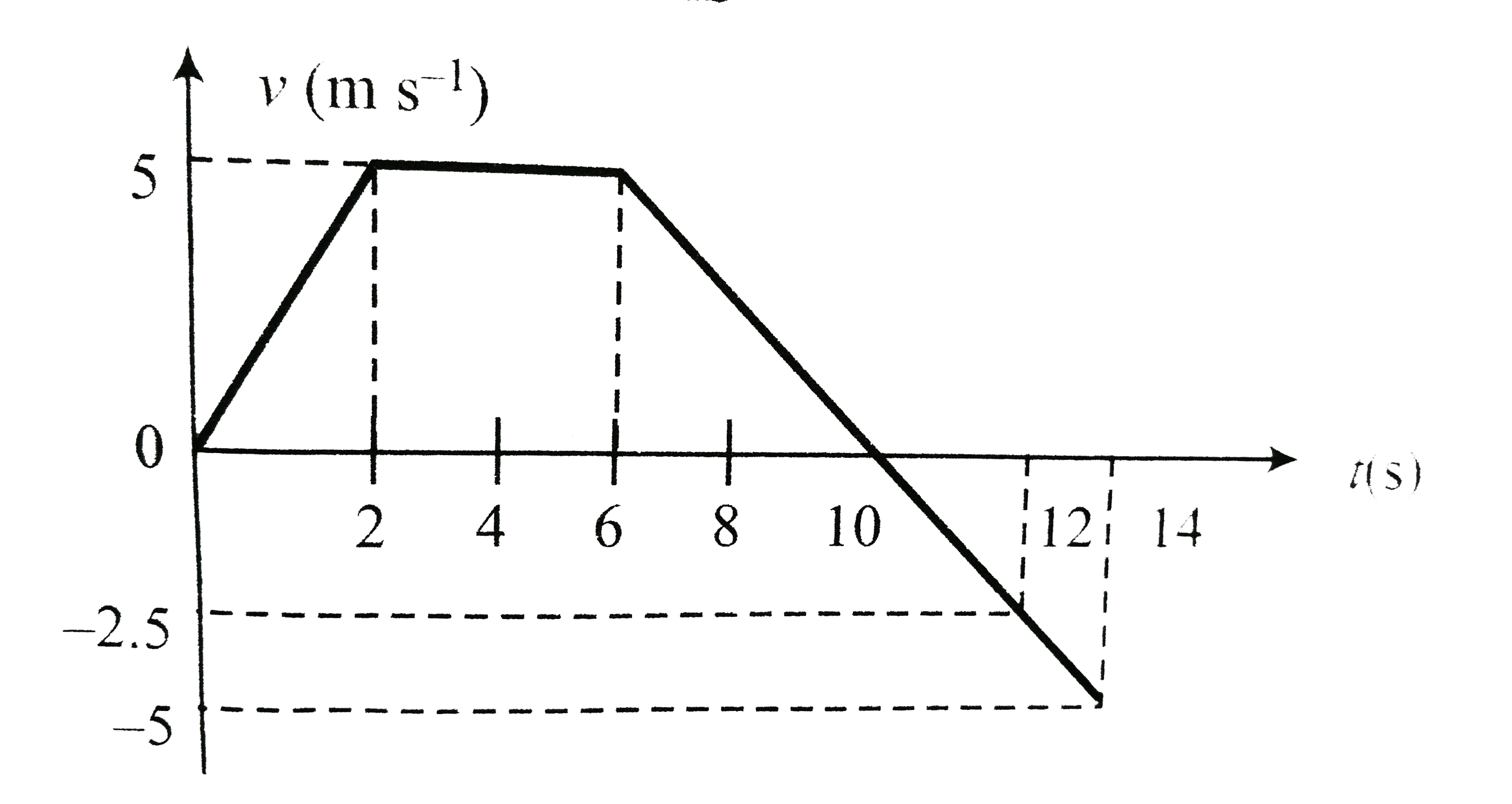 .View Solution
.View SolutionA body starting with a velocity 'v' returns to its initial position after 't' second with the same speed, along the same line. Acceleration of the particle is
View SolutionIf a particle starts moving with initial velocity u=1ms−1 and acceleration a=2ms−2, the veloctiy of the particle at any time is given by v=u+at=1+2t. Plot the velocity-time graph of the particle.
View SolutionThe acceleration of a particle which moves along the positive x-axis varies with its position as shown in figure. If the velocity of the particle is 0.8ms−1 at x = 0, then velocity of the particle at x=1.4m is (∈ms−1).
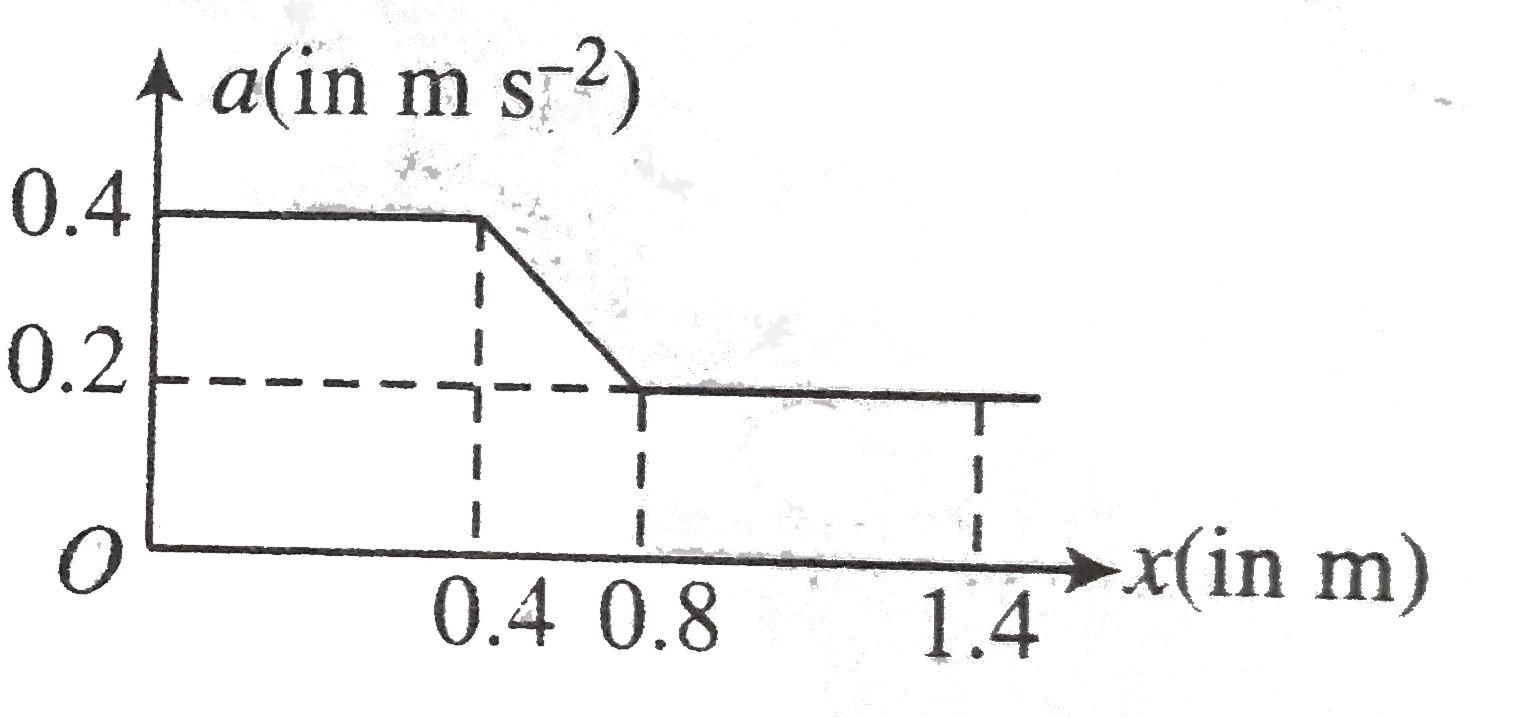 View Solution
View SolutionA particle of charge −16×10−18 coulomb moving with velocity 10ms−1 along the x− axis , and an electric field of magnitude 104/(m) is along the negative z− axis. If the charged particle continues moving along the x- axis , the magnitude of B is
View Solution
