A charged particle enters a magnetic field at right angles to the field. The field exists for a length equal to 1.5 times the radius of circular path of particle. The particle will be deviated from its path by
90∘
sin−1(2/3)
30∘
180∘
The correct Answer is:D
To solve the problem of how much a charged particle is deviated from its path when it enters a magnetic field at right angles, we can follow these steps:
Step 1: Understand the Motion of the Charged Particle
When a charged particle enters a magnetic field at right angles, it experiences a magnetic force that causes it to move in a circular path. The radius of this circular path can be determined using the formula:
r=mvqB
where:
- m is the mass of the particle,
- v is the velocity of the particle,
- q is the charge of the particle,
- B is the magnetic field strength.
Step 2: Determine the Length of the Magnetic Field
The problem states that the magnetic field exists for a length equal to 1.5 times the radius of the circular path. Hence, the length of the magnetic field L can be expressed as:
L=1.5r
Step 3: Calculate the Maximum Displacement
The maximum displacement xmax of the particle while it is within the magnetic field can be calculated. Since the particle moves in a circular path, the maximum deviation from the original path will be equal to the radius r when it exits the magnetic field:
xmax=r
Step 4: Relate the Length of the Magnetic Field to the Circular Path
Since the magnetic field length is 1.5r, and the maximum displacement xmax is equal to r, we can see that the particle will not complete a full circular path before exiting the magnetic field. Instead, it will deviate by a distance equal to the radius r.
Step 5: Determine the Angle of Deviation
When the particle exits the magnetic field, it will reverse its direction. The initial direction of the particle is perpendicular to the magnetic field, and upon exiting, it will be directed opposite to its initial path. This results in a deviation of:
Φ=180∘
Conclusion
Thus, the charged particle will be deviated from its path by an angle of 180∘.
Final Answer
The particle will be deviated from its path by 180∘.
When a charged particle enters a magnetic field at right angles, it experiences a magnetic force that causes it to move in a circular path. The radius of this circular path can be determined using the formula:
r=mvqB
where:
- m is the mass of the particle,
- v is the velocity of the particle,
- q is the charge of the particle,
- B is the magnetic field strength.
The problem states that the magnetic field exists for a length equal to 1.5 times the radius of the circular path. Hence, the length of the magnetic field L can be expressed as:
L=1.5r
The maximum displacement xmax of the particle while it is within the magnetic field can be calculated. Since the particle moves in a circular path, the maximum deviation from the original path will be equal to the radius r when it exits the magnetic field:
xmax=r
Since the magnetic field length is 1.5r, and the maximum displacement xmax is equal to r, we can see that the particle will not complete a full circular path before exiting the magnetic field. Instead, it will deviate by a distance equal to the radius r.
When the particle exits the magnetic field, it will reverse its direction. The initial direction of the particle is perpendicular to the magnetic field, and upon exiting, it will be directed opposite to its initial path. This results in a deviation of:
Φ=180∘
Thus, the charged particle will be deviated from its path by an angle of 180∘.
The particle will be deviated from its path by 180∘.
Topper's Solved these Questions
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Only One Option is Correct
45 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - More than One Option is Correct
25 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
- MEASUREMENT AND ERRORSBOOK - DC PANDEY ENGLISHCHAPTER - MEASUREMENT AND ERRORSEXERCISE - Subjective
19 Videos
Similar Questions
A charged particle enters a uniform magnetic field perpendicular to it. The magnetic field
View SolutionWhen a charged particle enters a uniform magnetic field its kinetic energy
View SolutionIf a charged particle enters perpendicular in the uniform magnetic field then
View SolutionA charged particle is moved along a magnetic field line. The magnetic force on the particle is
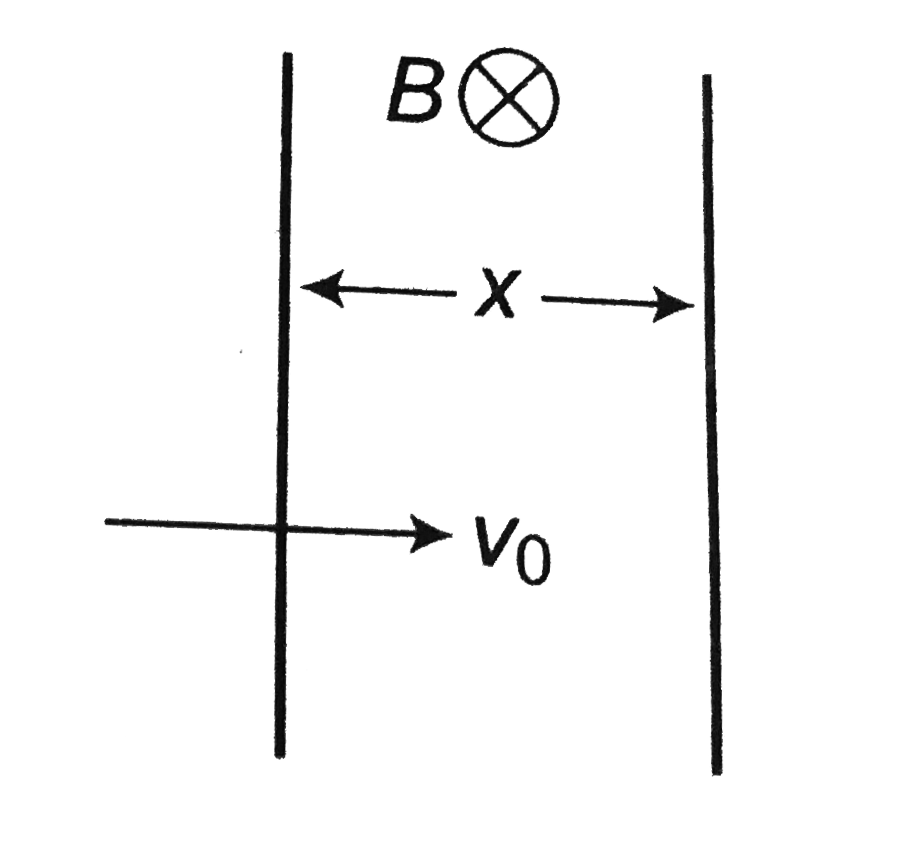
View SolutionA charged particle enters into a uniform magnetic field with velocity v0 perpendicular to it , the length of magnetic field is x=√32R, where R is the radius of the circular path of the particle in the field .The magnitude of charge in velocity of the particle when it comes out of the field is
View SolutionPositively charged particles are projected into a magnetic field. If the direction of the magnetic field is along the direction of motion of the charged particles, the particles get
View SolutionA proton and an alpha particle both enters a region of uniform magnetic field B, moving at right angles to the field B. If the radius of circular orbits for both the particles is equal and the kinetic energy acquired by proton is 1MeV, the energy acquired by the alpha particles will be :
View SolutionA charged particle enters in a magnetic field B with its initial velocity making an angle of 45° with B. The path of the particle will be
View SolutionThe cyclotron is a device which is used to accelerate charged particles such as protons, deutrons, alpha particles, etc. to very high energy. The principle on which a cyclotron works is based on the fact that an electric field can accelerate a charged particle and a magnetic field can throw it into a circular orbit. A particle of charge +q experiences a force qE in an electric field E and this force is independent of velocity of the particle. The particle is accelerated in the direction of the magnetic field. On the other hand, a magnetic field at right angles to the direction of motion of the particle throws the particle in a circular orbit in which the particle revolves with a frequency that does not depend on its speed. A modest potential difference is used as a sources of electric field. If a charged particle is made to pass through this potential difference a number of times, it will acquire an enormous by large velocity and hence kinetic energy.
Which of the following cannot be accelerated in a cyclotron?
View SolutionThe cyclotron is a device which is used to accelerate charged particles such as protons, deutrons, alpha particles, etc. to very high energy. The principle on which a cyclotron works is based on the fact that an electric field can accelerate a charged particle and a magnetic field can throw it into a circular orbit. A particle of charge +q experiences a force qE in an electric field E and this force is independent of velocity of the particle. The particle is accelerated in the direction of the magnetic field. On the other hand, a magnetic field at right angles to the direction of motion of the particle throws the particle in a circular orbit in which the particle revolves with a frequency that does not depend on its speed. A modest potential difference is used as a sources of electric field. If a charged particle is made to pass through this potential difference a number of times, it will acquire an enormous by large velocity and hence kinetic energy.
The working of a cyclotron is based on the fact that
View Solution
