A charged particle of unit mass and unit charge moves with velocity →v=(8ˆi+6ˆj)ms−1 in magnetic field of →B=2ˆkT. Choose the correct alternative (s).
The path of the particle may be x2+y2−4x−21=0
The path of the particle may be x2+y2=25
The path of the particle may be y2+z2=25
The time period of the particle will be 3.14 s
The correct Answer is:A, B, D
To solve the problem step by step, we will analyze the motion of a charged particle in a magnetic field.
Step 1: Identify the given quantities
- Velocity of the particle: →v=8^i+6^jm/s
- Magnetic field: →B=2^kT
- Mass of the particle: m=1kg (unit mass)
- Charge of the particle: q=1C (unit charge)
Step 2: Calculate the magnitude of the velocity
The magnitude of the velocity |→v| can be calculated using the formula:
|→v|=√(vx)2+(vy)2
Substituting the values:
|→v|=√(8)2+(6)2=√64+36=√100=10m/s
Step 3: Calculate the radius of the circular path
The radius R of the circular path of a charged particle moving in a magnetic field is given by the formula:
R=mvqB
Substituting the known values:
R=1⋅101⋅2=102=5m
Step 4: Calculate the time period of the motion
The time period T of the circular motion can be calculated using the formula:
T=2πmqB
Substituting the values:
T=2π⋅11⋅2=2π2=πs≈3.14s
Step 5: Analyze the path of the particle
The path of the particle can be described by the equation of a circle in the xy-plane. Since the radius is 5m, the equation can be written as:
x2+y2=R2=52=25
Conclusion
Based on the calculations, the radius of the circular path is 5m, and the time period of the motion is approximately 3.14s. The correct alternatives based on the derived equations are:
- The equation x2+y2=25 is correct.
- The time period T≈3.14s is also correct.
- Velocity of the particle: →v=8^i+6^jm/s
- Magnetic field: →B=2^kT
- Mass of the particle: m=1kg (unit mass)
- Charge of the particle: q=1C (unit charge)
The magnitude of the velocity |→v| can be calculated using the formula:
|→v|=√(vx)2+(vy)2
Substituting the values:
|→v|=√(8)2+(6)2=√64+36=√100=10m/s
The radius R of the circular path of a charged particle moving in a magnetic field is given by the formula:
R=mvqB
Substituting the known values:
R=1⋅101⋅2=102=5m
The time period T of the circular motion can be calculated using the formula:
T=2πmqB
Substituting the values:
T=2π⋅11⋅2=2π2=πs≈3.14s
The path of the particle can be described by the equation of a circle in the xy-plane. Since the radius is 5m, the equation can be written as:
x2+y2=R2=52=25
Based on the calculations, the radius of the circular path is 5m, and the time period of the motion is approximately 3.14s. The correct alternatives based on the derived equations are:
- The equation x2+y2=25 is correct.
- The time period T≈3.14s is also correct.
Topper's Solved these Questions
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SCQ_TYPE
5 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE
1 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SUBJECTIVE_TYPE
1 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery
59 Videos
- MAGNETISM AND MATTERBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETISM AND MATTEREXERCISE - Medical gallery
1 Videos
Similar Questions
A charged particle of specific charge α moves with a velocity →v=v0ˆi in a magnetic field →B=B0√2(ˆj+ˆk). Then (specific charge=charge per unit mass)
View SolutionA charge particle of charge q and mass m is moving with velocity v as shown in fig In a uniform magnetic field B along -ve z-direction.Select the correct alternative (s).
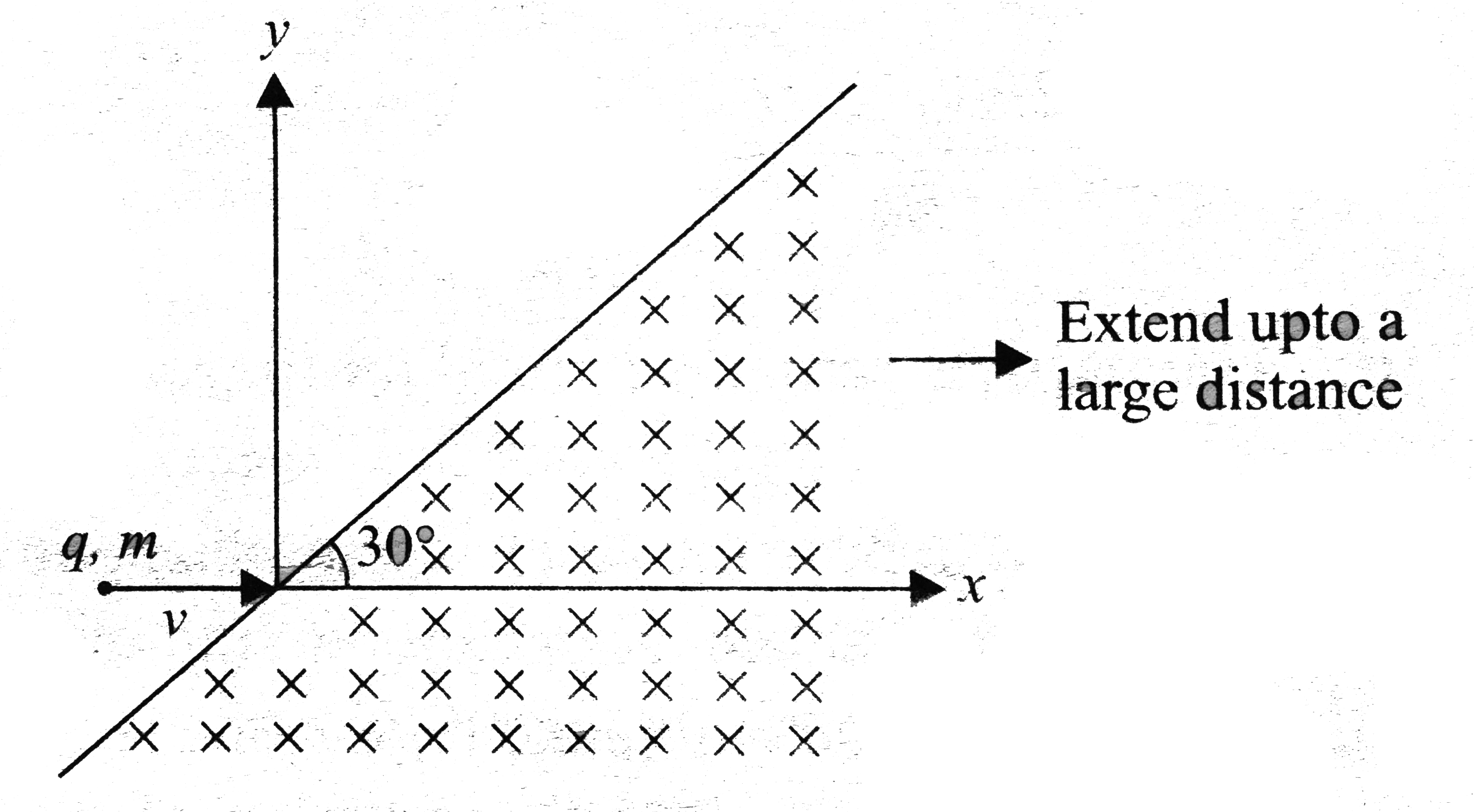
View Solution
Knowledge Check
An electron is moving with an initial velocity →v=v0ˆi and is in a magnetic field →B=B0ˆj. Then it's de-Broglie wavelength
Aremains constantBincreases with timeCdecreases with timeDincreases and decreases periodically
A particle of charge per unit mass α is released from origin with a velocity →v=v0ˆi uniform magnetic field →B=−B0ˆk. If the particle passes through (0,y,0), then y is equal to
View SolutionAn electron is moving with an initial velocity →v=v0ˆi and is in a magnetic field →B=B0ˆj. Then it's de-Broglie wavelength
View SolutionAnswer the following:
(a) Write the expression for the force →F acting on a particle of mass m and charge q moving with velocity→V in a magnetic field →B . Under what conditions will it move in
(i) a circular path and (ii) a helical path ?
(b) Show that the kinetic energy of the particle moving a magnetic field remains constant.
View SolutionA positive charge particle having change q and mass m has velocity →v=v(ˆi+ˆk√2) in the magnetic field B at the origin . Its speed as the function of y is :
View SolutionWrite an expression in a vector form for the Lorentz magnetic force →F on a charge Q moving with velocity →V in a magnetic field →B. What is the direction of the magnetic force?
View SolutionA charged particle carrying charge 1μC is moving with velocity (2ˆi+3ˆi+4ˆk)ms−1. If an external magnetic field of (5ˆi+3ˆj−6ˆk)×10−3T exists in the region where the particle is moving then the force on the particle is →F×10−9N. The vector →F is :
View Solution1microC charge moves with the velocity →v=4ˆi+6ˆj+3ˆk in uniform magnetic field, →B=3ˆi+4ˆj−3ˆkxx 10^(-3). Force experience by charged particle in units of 10^(-9) N will be,
View Solution
