A circular disc is rotating with an angular speed (in radian per sec)
given,
In terms of and at
find,
(a).
(b).
(c). linear velocity of the particle lying at (d). linear acceleration of the particle lying
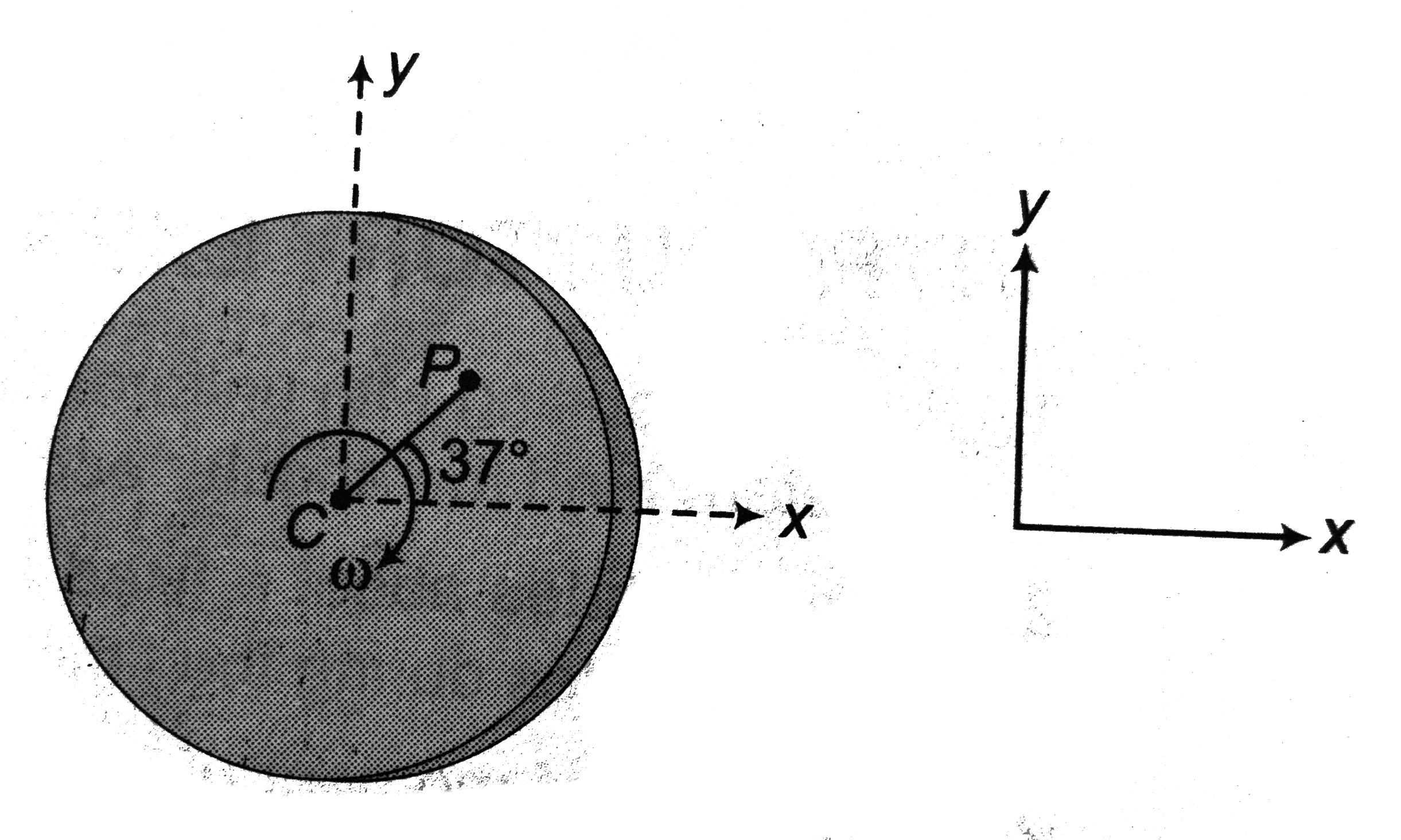
at , and
for the particle at ,
(a). Rotation is clockwise. So according to right hand rule is perpendicular to paper inwards along negative z-direction
(b). is increasing. so is alos in the direction of
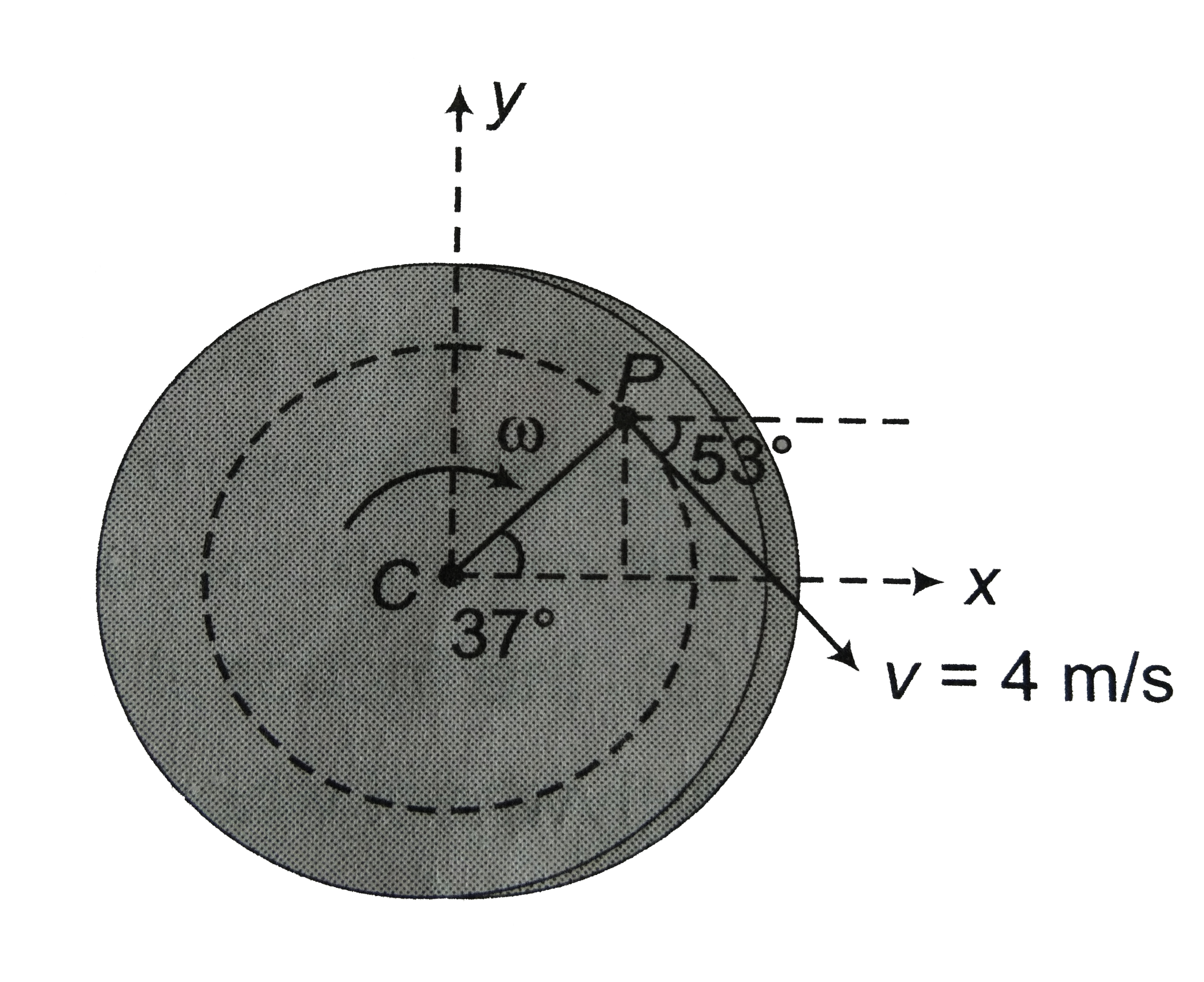
(c).
This velocity is tangential to the doted circle of as shown in figure.
or
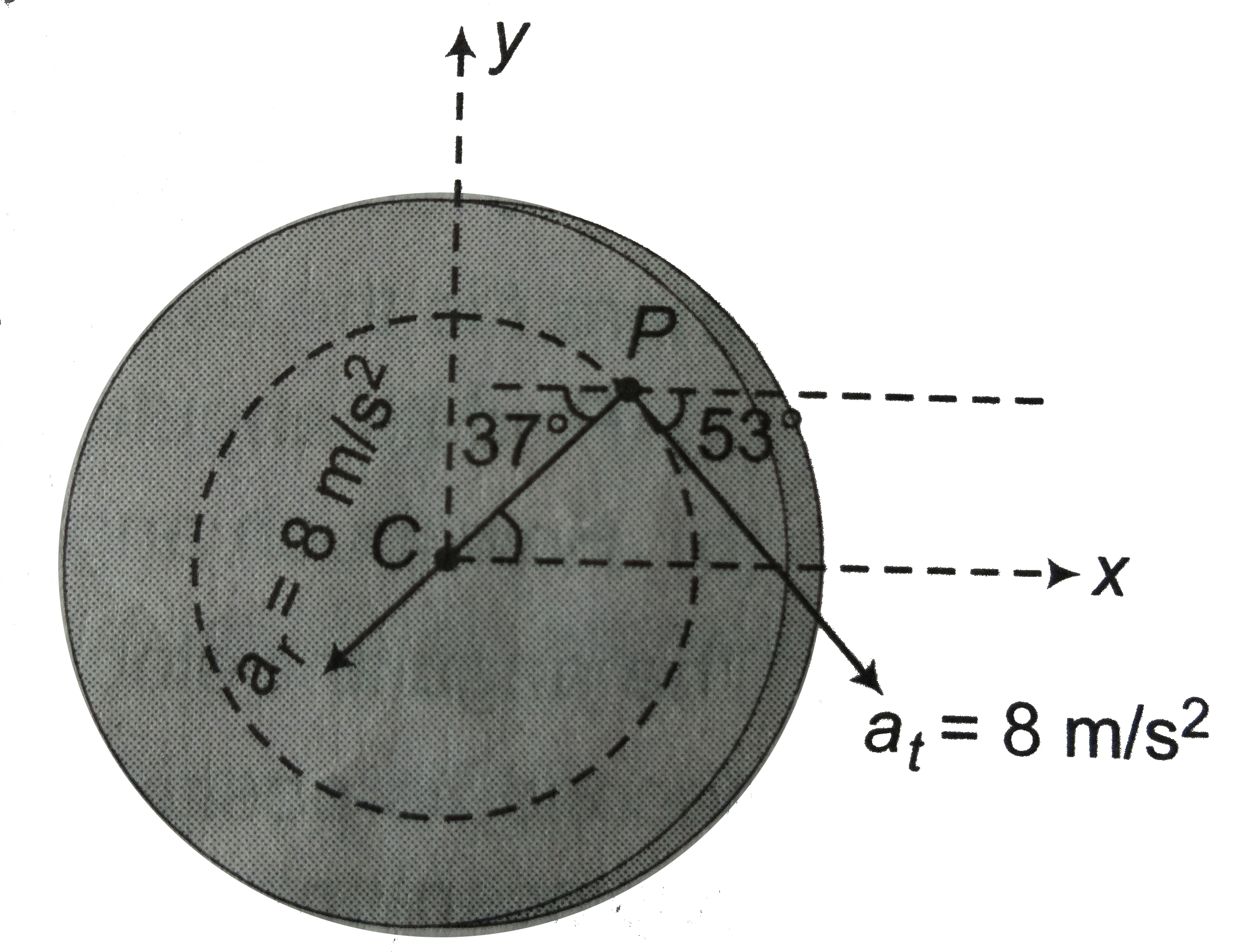
(d). Acceleration of the particle has two components
(i). (radial component)
this components is towareds centre C.
(ii). (tangential component)
this component is in the direction of linear velocity, as or is increasing
or
Topper's Solved these Questions
- ROTATIONAL MECHANICSBook:DC PANDEYChapter:ROTATIONAL MECHANICSExercise:Solved Examples
Explore 25 Videos
- ROTATIONAL MECHANICSBook:DC PANDEYChapter:ROTATIONAL MECHANICSExercise:Miscellaneous Examples
Explore 2 Videos
- ROTATIONBook:DC PANDEYChapter:ROTATIONExercise:(C) Chapter Exercises
Explore 39 Videos
- ROTATIONAL MOTIONBook:DC PANDEYChapter:ROTATIONAL MOTIONExercise:Integer Type Questions
Explore 17 Videos
Similar Questions
Knowledge Check
If velocity of a particle is given by v=2t2−2 then find the acceleration of particle at t = 2 s.
A0B2C4D8Velocity of a particle is given as v=(2t2−3)m/s. The acceleration of particle at t = 3s will be :
A18ms−2B12ms−2C15ms−2Dzerothe angular velocity omega of a particle varies with time t as ω=5t2+25rads. the angular acceleration of the particle att=1s is
A10rads2B5rads2CZeroD3rads2
The radius vector →r=2i+5k and the angular velocity of a particle is →w=3i−4k Then the linear velocity of the particle is
View SolutionA particle is revolving in a circle of radius 1 m with an angular speed of 12 rad/s. At t = 0, it was subjected to a constant angular acceleration α and its angular speed increased to (480π) rotation per minute (rpm) in 2 sec. Particle then continues to move with attained speed. Calculate
(i) angular acceleration of the particle,
(ii) tangential velocity of the particle as a function of time.
(iii) acceleration of the particle at t = 0.5 second and at t = 3 second
(iv) angular displacement at t = 3 second.
View Solution
In the figure shown υ=2m/s ω=5rad/s and CP=1m
In terms of ˆi and ˆj find linear velocity of particle P.
View SolutionVelocity vector of a particle is given as
→v=4tˆi+3ˆj
At t=0 position of the particle is given as →r0=2ˆj
Find the position vector of the particle at t=2 sec and te average acceleration of the particle for t=0 to t=2sec.
View Solution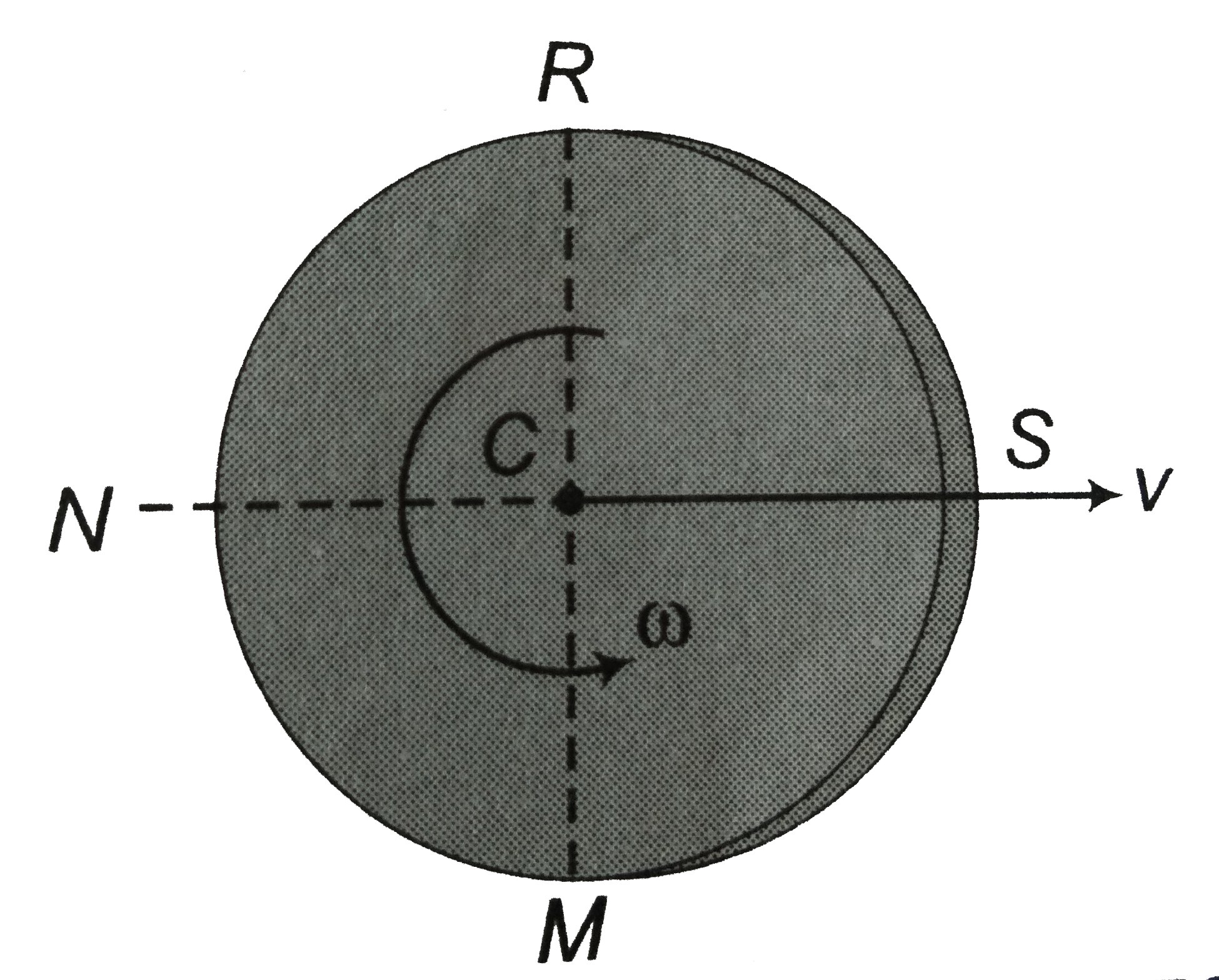
In the figure shown ω=v2R in terms of ˆi and ˆj find linear velocities of particles M, N, R and S.
View Solution