A circular hole of radius R/2 is cut from a circular disc of radius R. The disc lies in the xy-plane and its centre coincides with the origin. If the remaining mass of the disc is M, then
a. determine the initial mass of the disc and
b. determine its moment of inertia about the z-axis.
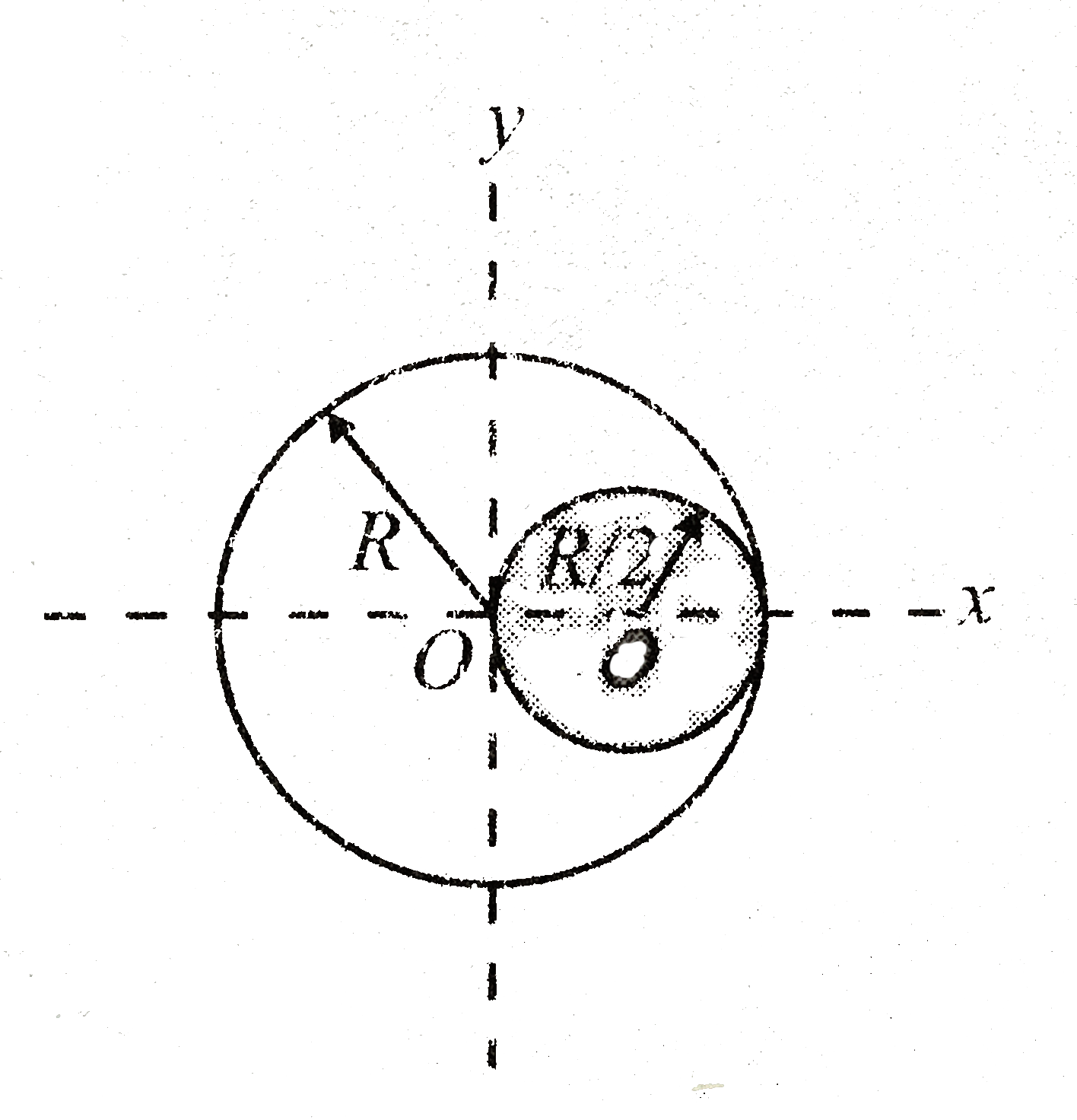
Let σ be the surface mass density of the plate given by
σ=M(πR2−π(R2))2=43MπR2
Now, initial mass of the plate m1=σ(πR2)=43M
mass of the plate removed m2=σ(πR24)=M3
The given arrangement may be considered as a combination of a circular plate of mass (4/3)M and circular plate of negative mass (M/3).

The moment of inertia of the big disc of radius R and mass m1 about O and parallel to the z-axis is
IO1=m1R22
The moment of inertia of the small disc of mass m2 and radius r2 about Oand parallel to z-axis.
IO1=m2(R2)22=m2R28
The moment of inertia of the small disc about O (using parallel axis theorem).
IO2=m2R28+m2R24=3m2R28
As the part of the disc on mass m2 is removed from disc m1, hence the net moment of inertia of structure is
IO=IO1=I(O2)
IO=m1R22−3m2R28
substituting the values of m1 and m2 we get
I0=1324MR2
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Solved Examples
9 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.1
6 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
Similar Questions
A circular disc of radius R is removed from a bigger circular disc of radius 2R such that the circumferences of the discs coincide. The center of mass of new disc is αR from the center of the bigger disc. The value of α is
View SolutionA concentric hole of radius R/2 is cut from a thin circular plate of mass M and radius R. The moment of inertia of the remaining plate about its axis will be
View SolutionA concentric hole of radius R/2 is cut from a thin circular plate of mass M and radius R. The moment of inertia of the remaining plate about its axis will be
View SolutionFrom a circular disc of radius R, a triangular portion is cut (sec figure). The distance of the centre of mass of the remainder from the centre of the disc is −

View SolutionA disc of radis R is cut out from a larger disc of radius 2R in such a way that the edge of the hole touches the edge of the disc. Locate the centre of mass of the residual disc.
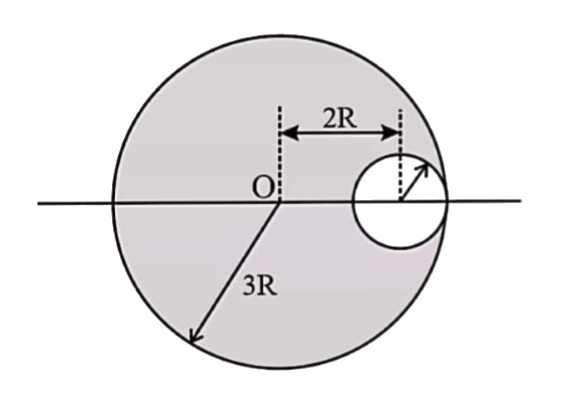
View SolutionThe figure shows a disc of radius 3R from which a circular hole of radius R is cut as shown in the figure. The distance of the centre of mass of the remaining object from the point O is
View SolutionA circular hole is cut from a disc of radius 6 cm in such a way that the radius of the hole is 1 cm and the centre of 3 cm from the centre of the disc. The distance of the centre of mass of the remaining part from the centre of the original disc is
View SolutionA disc of radius r is cut from a larger disc of radius 4r in such a way that the edge of the hole touches the edge of the disc. The centre of mass of the residual disc will be a distance from centre of larger disc :-
View SolutionA disc of radius r is cut from a larger disc of radius 4r in such a way that the edge of the hole touches the edge of the disc. The centre of mass of the residual disc will be a distance from centre of larger disc :-
View SolutionFrom a circular disc of radius R, a square is cut out with a radius as its diagonal. The center of mass of remaining portion is at a distance from the center)
View Solution
