A circular loop is kept perpendicular to a uniform magnetic field. Loop is rotated about its diameter with constant angular velocity.
Magnitude of emf induced will be minimum when magnitude of flux is maximum
Magnitude of emf is maximum when magnitude of flux is minimum
Phase difference between emf and flux is π2
None of these
The correct Answer is:A, B, C
To solve the problem of a circular loop rotating in a uniform magnetic field, we will analyze the situation step by step.
Step 1: Understand the Setup
A circular loop is placed perpendicular to a uniform magnetic field B. The loop is rotated about its diameter with a constant angular velocity ω.
Step 2: Define Magnetic Flux
The magnetic flux Φ through the loop is given by the formula:
Φ=B⋅A⋅cos(θ)
where:
- B is the magnetic field strength,
- A is the area of the loop,
- θ is the angle between the magnetic field and the normal to the surface of the loop.
Step 3: Determine the Angle θ
As the loop rotates, the angle θ changes with time. If the loop rotates with an angular velocity ω, then the angle at time t can be expressed as:
θ=ωt
Step 4: Write the Expression for Flux
Substituting θ into the flux equation, we have:
Φ(t)=B⋅A⋅cos(ωt)
Step 5: Apply Faraday's Law of Induction
According to Faraday's law, the induced electromotive force (EMF) E in the loop is given by the negative rate of change of magnetic flux:
E=−dΦdt
Step 6: Differentiate the Flux Expression
Now, we differentiate the flux with respect to time:
E=−ddt(B⋅A⋅cos(ωt))=BA⋅ω⋅sin(ωt)
Step 7: Analyze the Relationship Between EMF and Flux
From the expressions derived:
- The magnetic flux Φ(t)=BAcos(ωt)
- The induced EMF E=BAωsin(ωt)
Step 8: Determine Maximum and Minimum Values
1. The maximum value of the magnetic flux occurs when cos(ωt)=1 (i.e., Φmax=BA).
2. The induced EMF is maximum when sin(ωt)=1 (i.e., Emax=BAω).
3. The maximum flux occurs when the EMF is zero, and vice versa.
Step 9: Phase Difference
The sine and cosine functions are complementary:
- sin(ωt) reaches its maximum when cos(ωt) is zero, indicating a phase difference of π2 radians (or 90 degrees) between the EMF and the magnetic flux.
Conclusion
Based on the analysis, we can conclude:
1. The magnitude of EMF induced will be minimum when the magnitude of flux is maximum.
2. The magnitude of EMF is maximum when the magnitude of flux is minimum.
3. The phase difference between EMF and flux is π2.
Final Answer
Thus, the correct options are:
- A: Magnitude of EMF induced will be minimum when magnitude of flux is maximum.
- B: Magnitude of EMF is maximum when magnitude of flux is minimum.
- C: Phase difference between the EMF and flux is π2.
A circular loop is placed perpendicular to a uniform magnetic field B. The loop is rotated about its diameter with a constant angular velocity ω.
The magnetic flux Φ through the loop is given by the formula:
Φ=B⋅A⋅cos(θ)
where:
- B is the magnetic field strength,
- A is the area of the loop,
- θ is the angle between the magnetic field and the normal to the surface of the loop.
As the loop rotates, the angle θ changes with time. If the loop rotates with an angular velocity ω, then the angle at time t can be expressed as:
θ=ωt
Substituting θ into the flux equation, we have:
Φ(t)=B⋅A⋅cos(ωt)
According to Faraday's law, the induced electromotive force (EMF) E in the loop is given by the negative rate of change of magnetic flux:
E=−dΦdt
Now, we differentiate the flux with respect to time:
E=−ddt(B⋅A⋅cos(ωt))=BA⋅ω⋅sin(ωt)
From the expressions derived:
- The magnetic flux Φ(t)=BAcos(ωt)
- The induced EMF E=BAωsin(ωt)
1. The maximum value of the magnetic flux occurs when cos(ωt)=1 (i.e., Φmax=BA).
2. The induced EMF is maximum when sin(ωt)=1 (i.e., Emax=BAω).
3. The maximum flux occurs when the EMF is zero, and vice versa.
The sine and cosine functions are complementary:
- sin(ωt) reaches its maximum when cos(ωt) is zero, indicating a phase difference of π2 radians (or 90 degrees) between the EMF and the magnetic flux.
Based on the analysis, we can conclude:
1. The magnitude of EMF induced will be minimum when the magnitude of flux is maximum.
2. The magnitude of EMF is maximum when the magnitude of flux is minimum.
3. The phase difference between EMF and flux is π2.
Thus, the correct options are:
- A: Magnitude of EMF induced will be minimum when magnitude of flux is maximum.
- B: Magnitude of EMF is maximum when magnitude of flux is minimum.
- C: Phase difference between the EMF and flux is π2.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - COMPETITION FILE (MULTIPLE CHOICE QUESTIONS BASED ON GIVEN PASSAGE)
7 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - COMPETITION FILE (ASSERTION REASON TYPE QUESTIONS)
10 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - COMPETITION FILE (MULTIPLE CHOICE QUESTIONS) (AIPMT/NEET & Other State Boards for Medical Entrance)
8 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Chapter Practice Test
15 Videos
- ELECTROMAGNETIC WAVESBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST
14 Videos
Similar Questions
Current loop in a uniform magnetic field
View SolutionA planar wire loop is placed perpendicular to uniform magnetic field . Wire loop starts rotating in its own plane about its axis with uniform angular velocity ω. If B is magnetic field intensity then what will be the induced emf in the loop ?
View Solution
Knowledge Check
A circular loop of metal wire of radius r is placed perpendicular to uniform magnetic field B. Half of the loop is folded about the diameter with constant angular velocity ω. If resistance of the loop is R then current in the loop is
Azero, when θ=0Bπr2Bω2R when θ=0Cπr2Bω2R when θ=π6Dπr2Bω4R when θ=π6A uniform circular loop of radius a and resistance R palced perpendicular to a uniform magnetic field B. One half of the loop is rotated about the diameter with angular velocity ω as shown in Fig. Then, the current in the loop is
 A(a) zero, when θ is zeroB(b) πa2Bω2R, when θ is zeroC( c) zero, when θ=π/2D(d) πa2Bω2R, when θ=π/2
A(a) zero, when θ is zeroB(b) πa2Bω2R, when θ is zeroC( c) zero, when θ=π/2D(d) πa2Bω2R, when θ=π/2A copper rod of length l is rotated about one end perpendicular to the uniform magnetic field B with constant angular velocity ω . The induced e.m.f. between its two ends is
ABωl2B32Bωl2C12Bωl2D2Bωl2
As shown in Fig. 6.26, a rectangular loop and a circular loop are moving out of a uniform magnetic field region to a field free region with a constant velocity v. In which loop do you expect the induced emf to be constant during the passage out of the field region ? The field is normal to the loops.
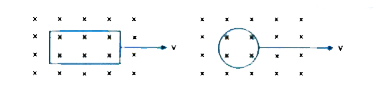
View SolutionA conducting circular loop of radius r is rotated about its diameter at a constant angular velocity ω in a magnetic field B perpendicular to the axis of rotation. In what position of the loop is the induced emf zero?
View SolutionA small loop of area of cross -section 10−4m2 is lying concentrically and coplanar inside a bigger loop of radius 0.628m. A current of 10A is passed in the bigger loop. The smaller loop is rotated about its diameter with an angular velocity ω. The magnetic flux linked with the smaller loop will be
View SolutionRadius of a circular loop placed in a perpendicular uniform magnetic field is increasing at a constant rate of roms−1 If at any instant radius of the loop is r, then emf induced in the loop at that instant will be
View SolutionRadius ol a circular luop placed in a perpendicular uniform magnetic field is increasing at a constant rate of roms1. If at any instant radius of the loop is r, then emf induced in the loop at that instant will be
View Solution
