A closed current-carrying loop having a current I is having area A. Magnetic moment of this loop is defined as where direction of area vector is towards the observer if current is flowing in anticlockwise direction with respect to the observer. If this loop is placed in a uniform magnetic field , then torque acting on the loop is given by . Now answer the following questions:
Let ring in the above question is having a radius R and a charge Q is uniformly distributed over it. Ring is rotated with a constant angular velocity as mentioned above.
Torque acting on the ring due to magnetic force is
None of the above
The correct Answer is:A
To solve the problem, we need to calculate the torque acting on a rotating ring with a uniformly distributed charge in a uniform magnetic field. Here's a step-by-step solution:
Step 1: Understand the Magnetic Moment
The magnetic moment (μ) of a current-carrying loop is given by the formula:
→μ=→IA
where I is the current and A is the area of the loop. For a ring of radius R, the area A is:
A=πR2
Step 2: Relate Charge to Current
The current I can be expressed in terms of the charge Q and the time period T of rotation:
I=QT
The time period T for one complete rotation at angular velocity ω is:
T=2πω
Thus, we can substitute T into the expression for current:
I=Qω2π
Step 3: Calculate the Magnetic Moment
Now substituting I and A into the magnetic moment formula:
μ=I⋅A=(Qω2π)⋅(πR2)=QωR22
Step 4: Calculate the Torque
The torque τ acting on the loop in a magnetic field →B is given by:
→τ=→μ×→B
The magnitude of the torque can be expressed as:
τ=μBsinθ
where θ is the angle between the magnetic moment vector and the magnetic field vector.
Step 5: Substitute the Magnetic Moment
Substituting the expression for μ into the torque equation:
τ=(QωR22)Bsinθ
Step 6: Special Cases
- If the magnetic field →B is perpendicular to the area vector (i.e., θ=90∘), then sinθ=1:
τ=QωR2B2
- If the magnetic field is at some other angle, the torque will be less than this maximum value.
Final Expression
Thus, the torque acting on the ring due to the magnetic force is:
τ=QωR2B2sinθ
The magnetic moment (μ) of a current-carrying loop is given by the formula:
→μ=→IA
where I is the current and A is the area of the loop. For a ring of radius R, the area A is:
A=πR2
The current I can be expressed in terms of the charge Q and the time period T of rotation:
I=QT
The time period T for one complete rotation at angular velocity ω is:
T=2πω
Thus, we can substitute T into the expression for current:
I=Qω2π
Now substituting I and A into the magnetic moment formula:
μ=I⋅A=(Qω2π)⋅(πR2)=QωR22
The torque τ acting on the loop in a magnetic field →B is given by:
→τ=→μ×→B
The magnitude of the torque can be expressed as:
τ=μBsinθ
where θ is the angle between the magnetic moment vector and the magnetic field vector.
Substituting the expression for μ into the torque equation:
τ=(QωR22)Bsinθ
- If the magnetic field →B is perpendicular to the area vector (i.e., θ=90∘), then sinθ=1:
τ=QωR2B2
- If the magnetic field is at some other angle, the torque will be less than this maximum value.
Thus, the torque acting on the ring due to the magnetic force is:
τ=QωR2B2sinθ
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer12videos
MISCELLANEOUS VOLUME 5
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Multiple Correct34videos
MISCELLANEOUS VOLUME 5
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False3videos
MISCELLANEOUS VOLUME 3
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - ddp.5.514videos
NUCLEAR PHYSICS
Similar Questions
A closed current-carrying loop having a current I is having area A. Magnetic moment of this loop is defined as →μ=−→IA where direction of area vector is towards the observer if current is flowing in anticlockwise direction with respect to the observer. If this loop is placed in a uniform magnetic field →B, then torque acting on the loop is given by →τ=→μ×→B. Now answer the following questions:
A uniformly charged insulating ring is rotated in a uniform magnetic field about its own axis, thenView SolutionA closed current-carrying loop having a current I is having area A. Magnetic moment of this loop is defined as →μ=−→IA where direction of area vector is towards the observer if current is flowing in anticlockwise direction with respect to the observer. If this loop is placed in a uniform magnetic field →B, then torque acting on the loop is given by →τ=→μ×→B. Now answer the following questions:
Consider the situation shown in Fig., ring is having a uniformly distributed positive charge. Magnetic field is perpendicular to the axis of ring. Now ring is rotated in anticlockwise direction as seen from left hand side direction of magnetic torque acting on the ring is
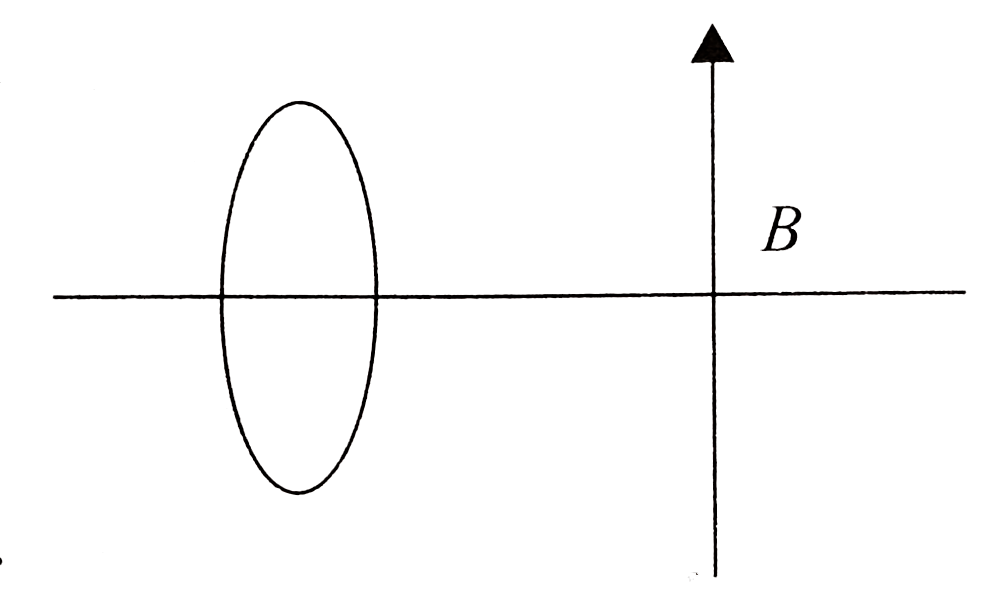 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A current carrying loop is placed in a uniform magnetic field. The torque acting on it does not depend upon
Aarea of loopBvalue of currentCmagnetic fieldDNone of these
A dipole of dipole moment →P is placed in uniform electric field →E, then torque acting on it is given by
View SolutionIn non-uniform magnetic field in certain direction, current loop is placed
View SolutionA current loop of arbitrary shape lies in a uniform magnetic field B. show that the net magnetic force acting on the loop is zero.
View SolutionTorque acting on a current loop in a uniform magnetic field is equal to
View SolutionA wire loop carrying current I is placed in the x−y plane as shown in the figure. If an external uniform magnetic field →B=Bˆi is switched on, then the torque acting on the loop is
 View Solution
View SolutionA current carrying loop in a uniform magnetic field will experience
View SolutionThe magnetic flux linked with a vector area →A in a uniform magnetic field →B is
View Solution
