A coin at the bottom of a trough containing water to a depth of 15 cm appears to be 3.75 cm raised above from the bottom. Calculate the refractive index of water.
To solve the problem of calculating the refractive index of water based on the given information about the coin in the trough, we can follow these steps:
Step 1: Understand the given information
- The real depth of the water (the actual depth of the trough) is given as 15 cm.
- The coin appears to be raised by 3.75 cm above the bottom of the trough.
Step 2: Calculate the apparent depth
The apparent depth can be calculated by subtracting the height by which the coin appears to be raised from the real depth.
Apparent Depth=Real Depth−Height Raised
Apparent Depth=15cm−3.75cm=11.25cm
Step 3: Use the formula for refractive index
The refractive index (μ) is given by the formula:
μ=Real DepthApparent Depth
Step 4: Substitute the values into the formula
Now, substitute the real depth and the apparent depth into the formula:
μ=15cm11.25cm
Step 5: Calculate the refractive index
Perform the division:
μ=1511.25=1.3333≈1.33
Step 6: Conclusion
The refractive index of water is approximately 1.33.
---
- The real depth of the water (the actual depth of the trough) is given as 15 cm.
- The coin appears to be raised by 3.75 cm above the bottom of the trough.
The apparent depth can be calculated by subtracting the height by which the coin appears to be raised from the real depth.
Apparent Depth=15cm−3.75cm=11.25cm
The refractive index (μ) is given by the formula:
Now, substitute the real depth and the apparent depth into the formula:
Perform the division:
The refractive index of water is approximately 1.33.
Topper's Solved these Questions
- SELF ASSESSMENT PAPER -3BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER -3EXERCISE - SECTION .B.
37 Videos
- SELF ASSESSMENT PAPER -3BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER -3EXERCISE - SECTION-A
31 Videos
- SELF ASSESSMENT PAPER -2BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER -2EXERCISE - SECTION .B.
37 Videos
- SELF ASSESSMENT PAPER -5BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER -5EXERCISE - SECTION-B
35 Videos
Similar Questions
A small bulb (assumed to be a point source) is placed at the bottom of a tank containing water to a depth of 80cm. Find out the area of the surface of water through which light from the bulb can emerge. Take the value of refractive index of water to be 4/3.
View SolutionA coin is placed at the bottom of a beaker containing water (refractive index=4/3) at a depth of 12cm. By what height the coin appears to be raised when seen from vertical above ?
View Solution
Knowledge Check
A small bulb (assumed to be a point source) is placed at the bottom of a tank containing water to a depth of 80cm. Find out the area of the surface of water through which light from the bulb can emerge. Take the value of refractive index of water to be 4/3.
A2.6m2B3.6m2C4.2m2D5.8m2
A coin is placed at the bottom of a glass trough containing water (refractive index = 43 ) up to a height 20 cm. At what depth it will appear when it is viewed from air, vertically above the coin. Draw a suitable ray diagram in support of your answer.
View SolutionRaise in water level problems : A cylinderical tub of radius 12 cm contains water to a depth of 20cm. A spherical form ball of a radius 9 cm is dropped into the tub and thus the level of water is raised by H cm. What is the value of H?
View SolutionA plane mirror is fixed at the bottom of a tank containing water. A small object is kept at a height of 24 cm from the bottom and is viewed from a point vertically above it. The distance between the object and the image in the mirror as appears to the person is
View SolutionA concave mirror of radius of curvature h is placed at the bottom of a tank containing a liquid of refractive index μ upto a depth d. An object P is placed at height h above the bottom of the miror. Outside the liquid, an observer O views the object and its image in the mirror. The apparent distance between these two will be
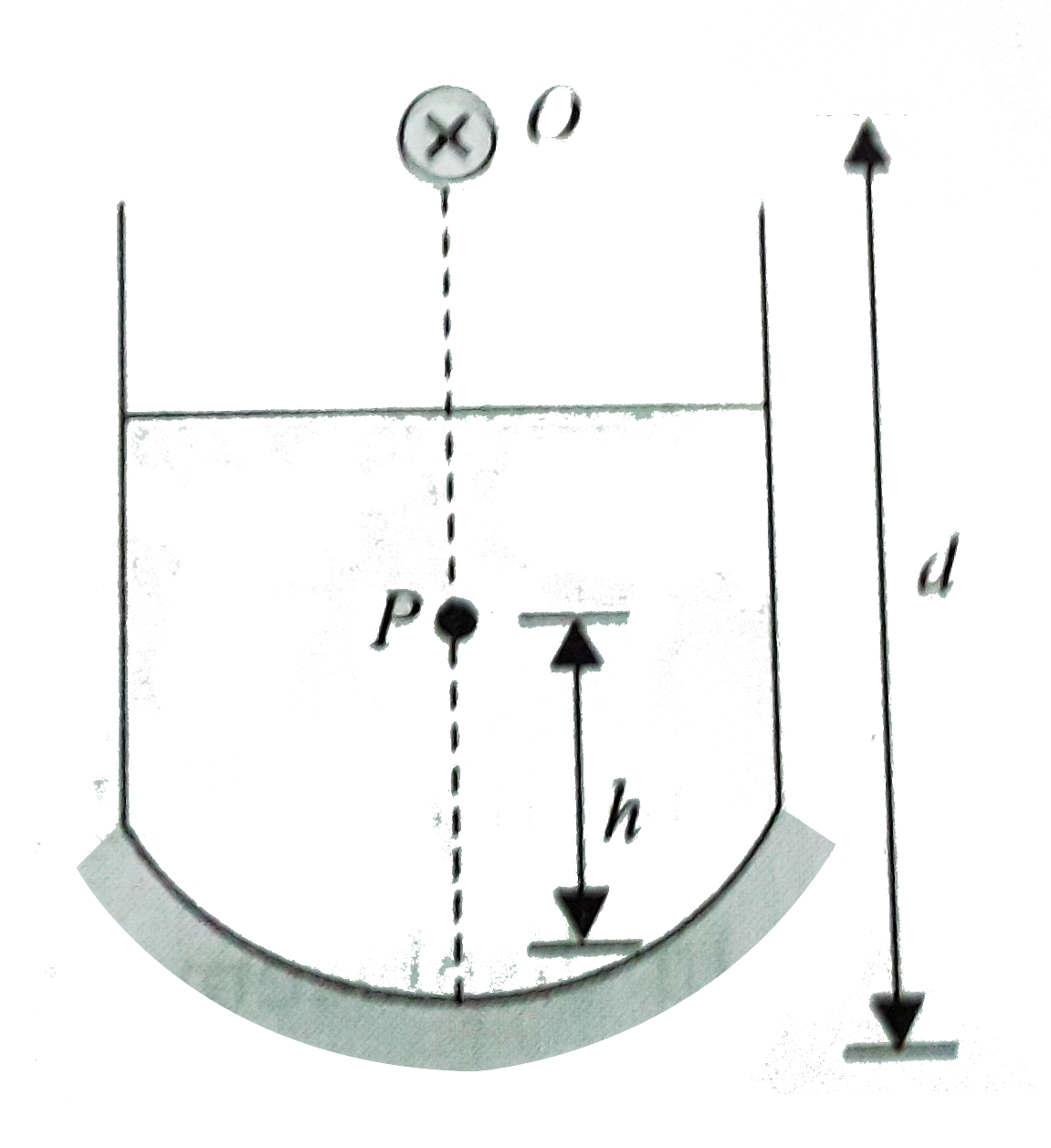
View SolutionA thin equiconvex lens of refractive index 3/2 is placed on a horizontal plane mirror as shown in figure. The space between the lens and the mirror is filled with a liquid of refractive index 4/3 . It is found that when a point object is placed 15 cm above the lens on its priincipal axis, the object coincides with its own image.

Q. If another liquid is filled instead of water, the object and the image coincide at a distance 25 cm from the lens.
Calculate the refractive index of the liquid.
View SolutionA vesserl contains a slab of glass 8cm thick and of refractive index 1.6 . Over the slab, the vessel is filled by oil of refractive index μ upto height 4.5 cm and then by another liquid, i.e., water of refractive index 4/3 and height 6cm as shown in Figure. An observer looking down from above observer that a mark at the bottom of glass slab appears to be raised up to a position 6cm from bottom of the slab. Find refractive index of oil (μ) .

View SolutionA point source of light is placed at the bottom of a water lake. If the area of the illuminated circle on the surface is equal to 3 times the square of the depth of the lake. The refractive index of water is
View Solution
