A coin placed on a rotating turntable just slips if it is placed at a distance of 4 cm from the centre. If the angular velocity of the turntable is doubled, it will just slip at a distance of
1cm
2cm
4cm
8cm
The correct Answer is:A
To solve the problem step by step, we will analyze the forces acting on the coin placed on the rotating turntable and how they change when the angular velocity is doubled.
1. Understand the Forces Acting on the Coin:
- When the coin is placed on the turntable, it experiences a centrifugal force due to the rotation, which is given by the formula:
Fc=mrω2
- Here, m is the mass of the coin, r is the distance from the center of the turntable, and ω is the angular velocity of the turntable.
- The centrifugal force is counteracted by the frictional force, which can be expressed as:
Ff=μsN
- Where μs is the coefficient of static friction and N is the normal force (which equals mg for horizontal surfaces).
2. Set Up the Equation for the Initial Condition:
- At the initial distance r=4 cm, the forces are balanced:
mrω2=μsmg
- Simplifying this by canceling m from both sides gives:
rω2=μsg
- This equation shows that the product rω2 is a constant.
3. Consider the New Condition When Angular Velocity is Doubled:
- When the angular velocity is doubled, we have ω′=2ω.
- We need to find the new distance r′ at which the coin will just slip:
mr′(2ω)2=μsmg
- This simplifies to:
r′⋅4ω2=μsg
4. Equate the Two Conditions:
- Since rω2=μsg is constant, we can equate the two conditions:
rω2=r′⋅4ω2
- Canceling ω2 from both sides gives:
r=4r′
5. Solve for the New Distance r′:
- We know that r=4 cm, so substituting this into the equation gives:
4=4r′
- Dividing both sides by 4 results in:
r′=1 cm
Final Answer:
The distance at which the coin will just slip when the angular velocity is doubled is 1 cm.
- When the coin is placed on the turntable, it experiences a centrifugal force due to the rotation, which is given by the formula:
Fc=mrω2
- Here, m is the mass of the coin, r is the distance from the center of the turntable, and ω is the angular velocity of the turntable.
- The centrifugal force is counteracted by the frictional force, which can be expressed as:
Ff=μsN
- Where μs is the coefficient of static friction and N is the normal force (which equals mg for horizontal surfaces).
- At the initial distance r=4 cm, the forces are balanced:
mrω2=μsmg
- Simplifying this by canceling m from both sides gives:
rω2=μsg
- This equation shows that the product rω2 is a constant.
- When the angular velocity is doubled, we have ω′=2ω.
- We need to find the new distance r′ at which the coin will just slip:
mr′(2ω)2=μsmg
- This simplifies to:
r′⋅4ω2=μsg
- Since rω2=μsg is constant, we can equate the two conditions:
rω2=r′⋅4ω2
- Canceling ω2 from both sides gives:
r=4r′
- We know that r=4 cm, so substituting this into the equation gives:
4=4r′
- Dividing both sides by 4 results in:
r′=1 cm
The distance at which the coin will just slip when the angular velocity is doubled is 1 cm.
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - HC VERMA ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Objective -2
6 Videos
- CIRCULAR MOTIONBOOK - HC VERMA ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Exercises
30 Videos
- CIRCULAR MOTIONBOOK - HC VERMA ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - worked out Examples
13 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective -2
11 Videos
- FLUID MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - All Questions
90 Videos
Similar Questions
A small objective placed on a rotating horizontal turn table just slips when it is placed at a distance 4cm from the axis of rotation. If the angular velocity of the trun-table doubled, the objective slip when its distance from the axis of ratation is.
View SolutionConstruct a tangent to a circle of radius 4cm from a point which is at a distance of 6 cm from its centre.
View Solution
Knowledge Check
A small objective placed on a rotating horizontal turn table just slips when it is placed at a distance 4cm from the axis of rotation. If the angular velocity of the trun-table doubled, the objective slip when its distance from the axis of ratation is.
A1cmB2cmC4cmD8cm
An object is placed at a distance of 12 cm from a convex lens of focal length 8 cm. Find :
the position of the image
View SolutionAn object is placed at a distance of 12 cm from a convex lens of focal length 8 cm. Find :
nature of the image
View SolutionAn object is placed at a distance 20 cm from the pole of a convex mirror of focal length 20 cm. The image is produced at
View SolutionA gramophone disc rotates at 60 rpm . A coin of mass 18 g is placed at a distance of 8 cm from the centre . Calculate centrifugal force on the coin . Take π2=9.87 .
View SolutionAn object is placed at a distance of 20 cm from a concave mirror of focal lenght 10 cm. What is the image distance?
View SolutionA coin is kept at distance of 10 cm from the centre of a circular turn table. If μ=0.8 the frequency of rotation at which the coin just begins to slip is
View SolutionA cylinder of height H and diameter H/4 is kept on a frictional turntable as shown in Fig. The axis of the cylinder is perpendicular to the surface of the table and the distance of axis of the cylinder is 2H from the centre of the table. The angular speed of the turntable at which the cylinder will start toppling (assume that friction is sufficient to prevent slipping) is
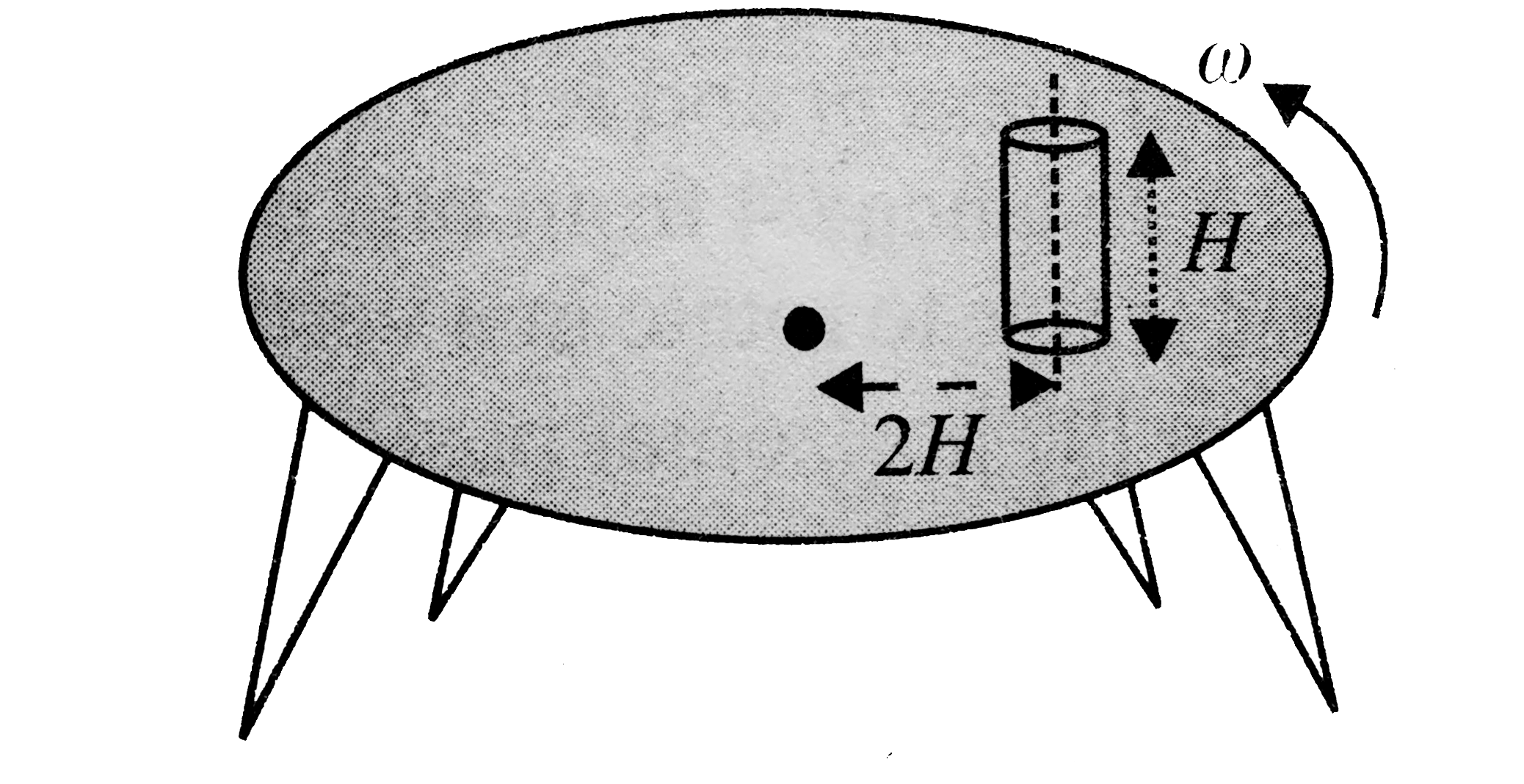
View Solution