A particle of mass m rotates with a uniform angular speed ω. It is viewed from a frame rotating about the Z-axis with a uniform angular speed ω0. The centrifugal force on the particler is
mω2a
mω2_0a
m(ω+ω02)2a
mωω0a
The correct Answer is:B
To solve the problem of finding the centrifugal force on a particle of mass m rotating with a uniform angular speed ω as viewed from a frame rotating about the Z-axis with a uniform angular speed ω0, we can follow these steps:
1. Understanding Centrifugal Force:
- Centrifugal force is a pseudo force that appears when observing motion from a rotating frame of reference. It acts outward on a mass moving in a circular path.
2. Identify the Acceleration of the Rotating Frame:
- The acceleration experienced by an object in a rotating frame is given by the formula:
a=ω20r
where r is the radius of the circular path of the particle.
3. Calculate the Centrifugal Force:
- The centrifugal force Fc can be calculated using the formula:
Fc=m⋅a
Substituting the expression for acceleration from step 2, we get:
Fc=m⋅(ω20r)
4. Final Expression:
- Thus, the centrifugal force acting on the particle is:
Fc=mω20r
Summary of the Solution:
The centrifugal force on the particle, as viewed from a rotating frame with angular speed ω0, is given by:
Fc=mω20r
- Centrifugal force is a pseudo force that appears when observing motion from a rotating frame of reference. It acts outward on a mass moving in a circular path.
- The acceleration experienced by an object in a rotating frame is given by the formula:
a=ω20r
where r is the radius of the circular path of the particle.
- The centrifugal force Fc can be calculated using the formula:
Fc=m⋅a
Substituting the expression for acceleration from step 2, we get:
Fc=m⋅(ω20r)
- Thus, the centrifugal force acting on the particle is:
Fc=mω20r
The centrifugal force on the particle, as viewed from a rotating frame with angular speed ω0, is given by:
Fc=mω20r
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - HC VERMA ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Objective -2
6 Videos
- CIRCULAR MOTIONBOOK - HC VERMA ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Exercises
30 Videos
- CIRCULAR MOTIONBOOK - HC VERMA ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - worked out Examples
13 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective -2
11 Videos
- FLUID MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - All Questions
90 Videos
Similar Questions
A thin circular disk of radius R is uniformly charged with density σ>0 per unit area.The disk rotates about its axis with a uniform angular speed ω.The magnetic moment of the disk is :
View SolutionA particle is rotating in circle with uniform speed as shown. The angular momentum of the particle w.r.t. origin is :-

View Solution
Knowledge Check
A solid cylinder of mass M and radius R rotates about its axis with angular speed ω. Its rotational kinetic energy is
A12MR2ω2BMR2ω2C14MR2ω2D18MR2ω2
A particle of mass m is observed from an inertial frame of reference and is found to move in a circle of radius r with a uniform speed v. The centrifugal force on it is
View SolutionA pendulum bob of mass m hangs from one end of a horizontal rod which is rotating about vertical axis with an unknown angular speed ω such that the light inextensible string of length l of the pedulum makes a constant angle θ with vertical. Find the
Q. angular speed ω
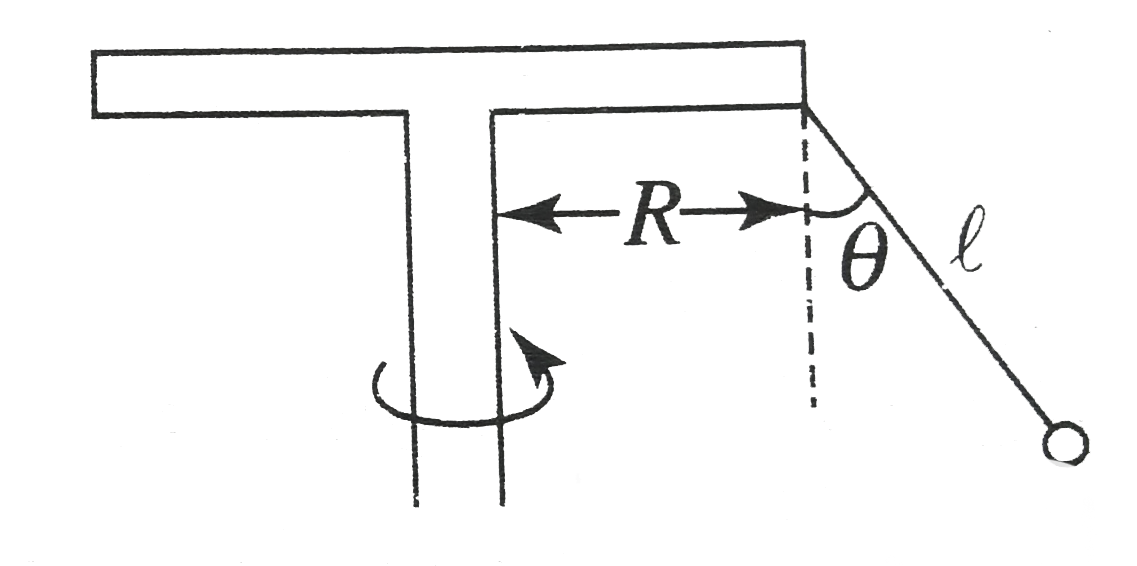
View SolutionA disc of mass m has a charge Q distributed on its surface. It is rotating about an XX' with a angular velocity ω. The force acting on the disc is

View SolutionA disc of the moment of inertia 'l1' is rotating in horizontal plane about an axis passing through a centre and perpendicular to its plane with constant angular speed 'ω1' . Another disc of moment of inertia 'I2'. having zero angular speed is placed discs are rotating disc. Now, both the discs are rotating with constant angular speed 'ω2'. The energy lost by the initial rotating disc is
View SolutionA rod is rotating with angular velocity ω about axis AB. Find cosθ.

View SolutionAngular momentum of a rigid body rotating about a fixed Axis with angular velocity →ω
View SolutionA particle is at rest with respect to the wall of an inverted cone rotating with uniform angular velocity ω about its central axis. The displacement of particle along the surface up or down, the equilibrium of particle is

View Solution
