A concave lens forms the image of an object such that the distance between the object and image is 10cm and the magnification produced is 1/4. The focal length of the lens will be
−6.2cm
−4.4cm
−8.6cm
−10cm
The correct Answer is:B
To find the focal length of a concave lens given the distance between the object and the image and the magnification, we can follow these steps:
1. Understand the given data:
- The distance between the object (O) and the image (I) is given as |u−v|=10cm.
- The magnification m=14.
2. Relate magnification to object and image distances:
- The magnification m is defined as:
m=vu
- Given m=14, we can write:
vu=14⟹v=14u
3. Substitute v in the distance equation:
- From the distance equation |u−v|=10, we substitute v:
u−14u=10
- This simplifies to:
34u=10
- Solving for u:
u=10×43=403cm
4. Calculate v:
- Now substitute u back to find v:
v=14u=14×403=103cm
5. Apply the sign convention:
- For a concave lens, the object distance u is taken as negative and the image distance v is also negative:
u=−403cm,v=−103cm
6. Use the lens formula to find the focal length:
- The lens formula is given by:
1f=1v−1u
- Substitute v and u:
1f=1−103−1−403
- This simplifies to:
1f=−310+340
- Finding a common denominator (which is 40):
1f=−1240+340=−940
- Therefore:
f=−409cm≈−4.44cm
Final Answer:
The focal length of the concave lens is f≈−4.44cm.
- The distance between the object (O) and the image (I) is given as |u−v|=10cm.
- The magnification m=14.
- The magnification m is defined as:
m=vu
- Given m=14, we can write:
vu=14⟹v=14u
- From the distance equation |u−v|=10, we substitute v:
u−14u=10
- This simplifies to:
34u=10
- Solving for u:
u=10×43=403cm
- Now substitute u back to find v:
v=14u=14×403=103cm
- For a concave lens, the object distance u is taken as negative and the image distance v is also negative:
u=−403cm,v=−103cm
- The lens formula is given by:
1f=1v−1u
- Substitute v and u:
1f=1−103−1−403
- This simplifies to:
1f=−310+340
- Finding a common denominator (which is 40):
1f=−1240+340=−940
- Therefore:
f=−409cm≈−4.44cm
The focal length of the concave lens is f≈−4.44cm.
Topper's Solved these Questions
- PRACTICE PAPPERBook:NCERT FINGERTPS ENGLISHChapter:PRACTICE PAPPERExercise:Practice Papper 2
Explore 50 Videos
- PRACTICE PAPPERBook:NCERT FINGERTPS ENGLISHChapter:PRACTICE PAPPERExercise:Practice Papper 3
Explore 50 Videos
- NUCLEIBook:NCERT FINGERTPS ENGLISHChapter:NUCLEIExercise:Assertion And Reason
Explore 15 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:NCERT FINGERTPS ENGLISHChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:NCERT Exemplar
Explore 11 Videos
Similar Questions
A cocave lens forms the image of an object such that the distance between the object and image is 10 cm and the magnification produced is 1/4. the focal length of the lens will be
View SolutionThe distance between an object and its upright image is 20cm. if the magnification is 0.5, what is the focal length of the lens that is being used to form the image?
View Solution
Knowledge Check
An object is place 20 cm from a diverging lens. If the distance between the lens and the image is 8 cm, what is the magnification?
A115B25C12D2
A convex lens is used to obtain a magnified image of an object on a screen . The object is at a distance 10 m from the lens . If the magnification is 19. the focal length of the lens is
View SolutionAn object is placed at a distance u from an equiconvex lens such that the distannce between the object and its real image is minimum. The focal length of the lens is f. The value of u is
View SolutionThe graph shown relationship between object distance and image distance for a equiconvex lens. Then focal length of the lens is
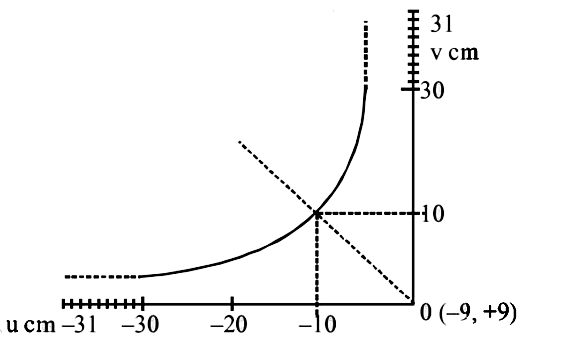
View SolutionAn extended real object of size 2cm is palced perpendicular to the principle axis of a converging lens of focal length 20cm. The distance between the object and the lens is 30cm
(i) Find the laterial magnification produced by the lens.
(ii) Find the height of the image.
View SolutionA convex lens of focal length f is placed somewhere in between an object and a screen. The distance between the object and the screen is x. If the numerical value of the magnification produced by the lens is m, then the focal lnegth oof the lens is .
View SolutionFind the distance of an object from a convex lens if image is
two times magnified. Focal length of the lens is 10cm
View SolutionFind the distance of an object from a convex lens if image is
two times magnified. Focal length of the lens is 10cm
View Solution