A concave mirror of radius 40 cm lies on a horizontla tale and wateis filled in it up t a heightof 5.00 cm. A small dust particle floats on the water surface at a point P vertically above tge pointof contact of the miror with the table. Locate the image of the dust particle as seen from a point directly above it. tEh refractie index of water is 1.33.
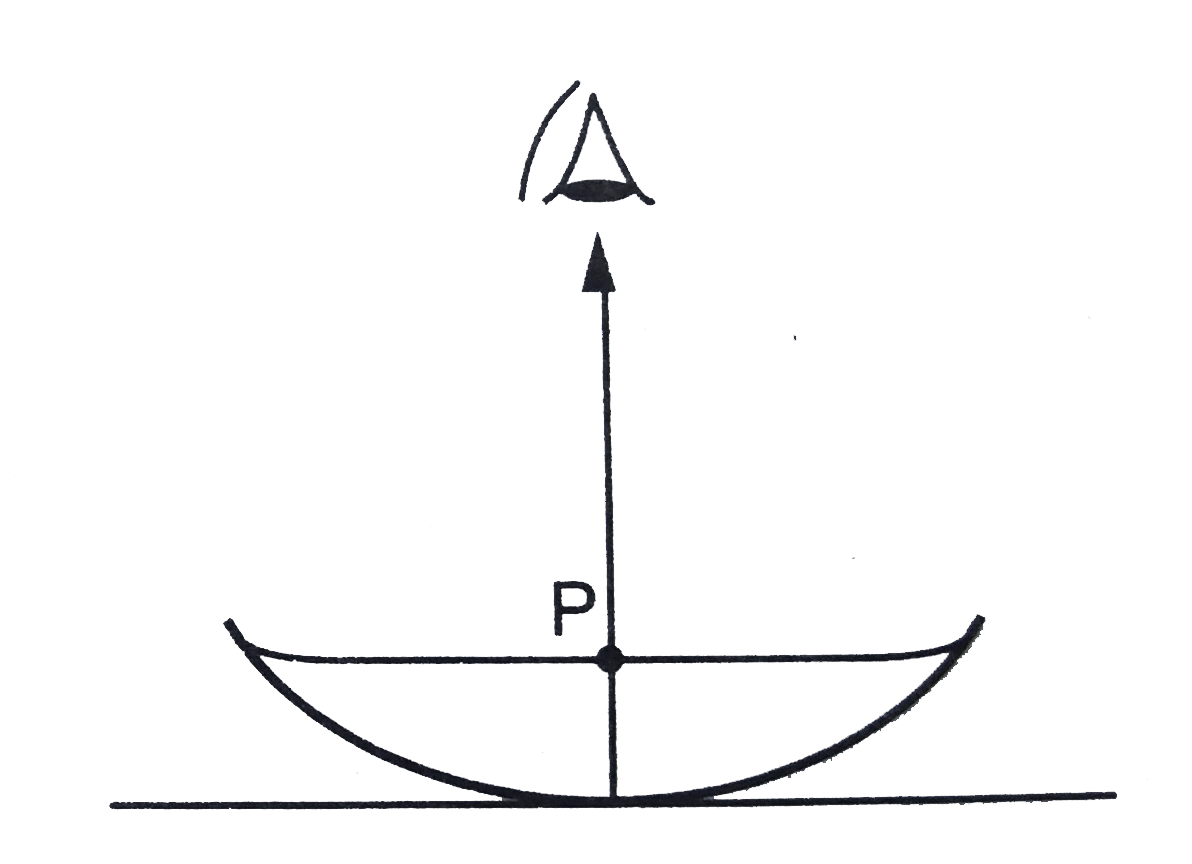


The dust particle is in water.
Image by concave mirror:
u=−5cm,f=−20cm,v=?
1v+1u=1f⇒1v+1−5=1−20⇒1v=15−120=320
v=203 cm
The image of P is formed at I.
Image by refraction:
After reflection direction of incident rays is reversed I serves as an object.
μ1=43,u=−(5+203)=−353cm
μ2=1,v=?
μ2v−μ1u=0
1v−43−353⇒v=−354=−8.75cm
Fiinal image is formed at I'.PI'=8.75cm.
Topper's Solved these Questions
- REFRACTION AT SPHERICAL SURFACESBOOK - CP SINGHCHAPTER - REFRACTION AT SPHERICAL SURFACESEXERCISE - EXERCISES
105 Videos
- REFLECTION OF LIGHTBOOK - CP SINGHCHAPTER - REFLECTION OF LIGHTEXERCISE - EXERCISES
67 Videos
- REFRACTION OF LIGHT BY PLANE SURFACESBOOK - CP SINGHCHAPTER - REFRACTION OF LIGHT BY PLANE SURFACESEXERCISE - Exercises
110 Videos
Similar Questions
A concave mirror of radius 40 cm lies on a horizontla tale and wateis filled in it up t a heightof 5.00 cm. A small dust particle floats on the water surface at a point P vertically above tge pointof contact of the miror with the table. Locate the image of the dust particle as seen from a point directly above it. tEh refractie index of water is 1.33.

View SolutionA point source of light is located at the bottom of a steel tank, and an opaque circular card of radius 6.00 cm is placed horizontally over it. A transparent fluid is gently added to the tank so that the card floats on the fluid surface with its center directly above the light source. No light is seen by an observer above the surface until the fluid is 5.00 cm deep. What is the index of refraction of the fluid ?
View Solution
Knowledge Check
A container is filled with water (μ=1.33) up to height of 33.2cm. A concave mirror is placed 15 cm above the water level. Image of an object placed at the bottom is formed at the same place. The focal length of mirror is :
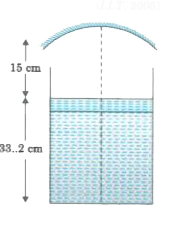 A10 cmB15 cmC-20 cmD2 cm
A10 cmB15 cmC-20 cmD2 cmA glass beaker is filled with water up to 5cm. It is kept on top of a 2cm thick glass slab. When a coin at the bottom of the glass slab is viewed at the normal incidence from above the beaker, its apparent depth from the water surface is dcm. Value of d is close (the refractive index of water and glass are 1.33 and 1.50,respectively)
A2.5B5.1C3.7D6Water is filled in a container upto a height of 5cm. There is a concave mirror of radius of curvature 40cm. A person just above the surface observes image of 'A'. The distance of image from water surface is (μwater=1.33):
_2019_CBT7_E01_003_Q01.png) A8.8cmB7.8C6.8D5.4
A8.8cmB7.8C6.8D5.4
A long cylindrical tube containing water in closed by an equinvex lens of local length 10 cm in air. A point source is placed along the axis of the tube outside it at a distance of 21 cm from the lens. Locate the final image of the source. Refractive index of the materials of the lens =1.5andtˆofwater=1.33.
View SolutionA small object is at the bottom of a container which has water filled up to a height of 20 cm. There is a plane mirror inclined at 45° to the horizontal above the container. A convex lens having focal length 15 cm is at a distance of 50 cm from the mirror. The horizontal principal axis of the lens is at a distance of 45 cm from the bottom of the container. Find the distance of the image (from the lens) of the object as seen by an observer to the left of the lens. Light rays from the object hit the lens only after they are reflected from the mirror. (use μwater=4/3)

View SolutionA transparent solid sphere of radius 2cm and density ρ floats in a transparent liquid of density 2ρ kept in a beaker. The bottom of the beaker is spherical in shape with radius of curvature 8cm and is silvered to make it concave mirror as shown in the figure. When an object is placed at a distance of 10cm directly above the centre of the sphere C, its final image coincides with it. Find h (as shown in the figure ), the height of the liquid surface in the beaker from the apex of the bottom. Consider the paraxial rays only. The refractive index of the sphere is 3/2 and that of the liquid is 4/3.
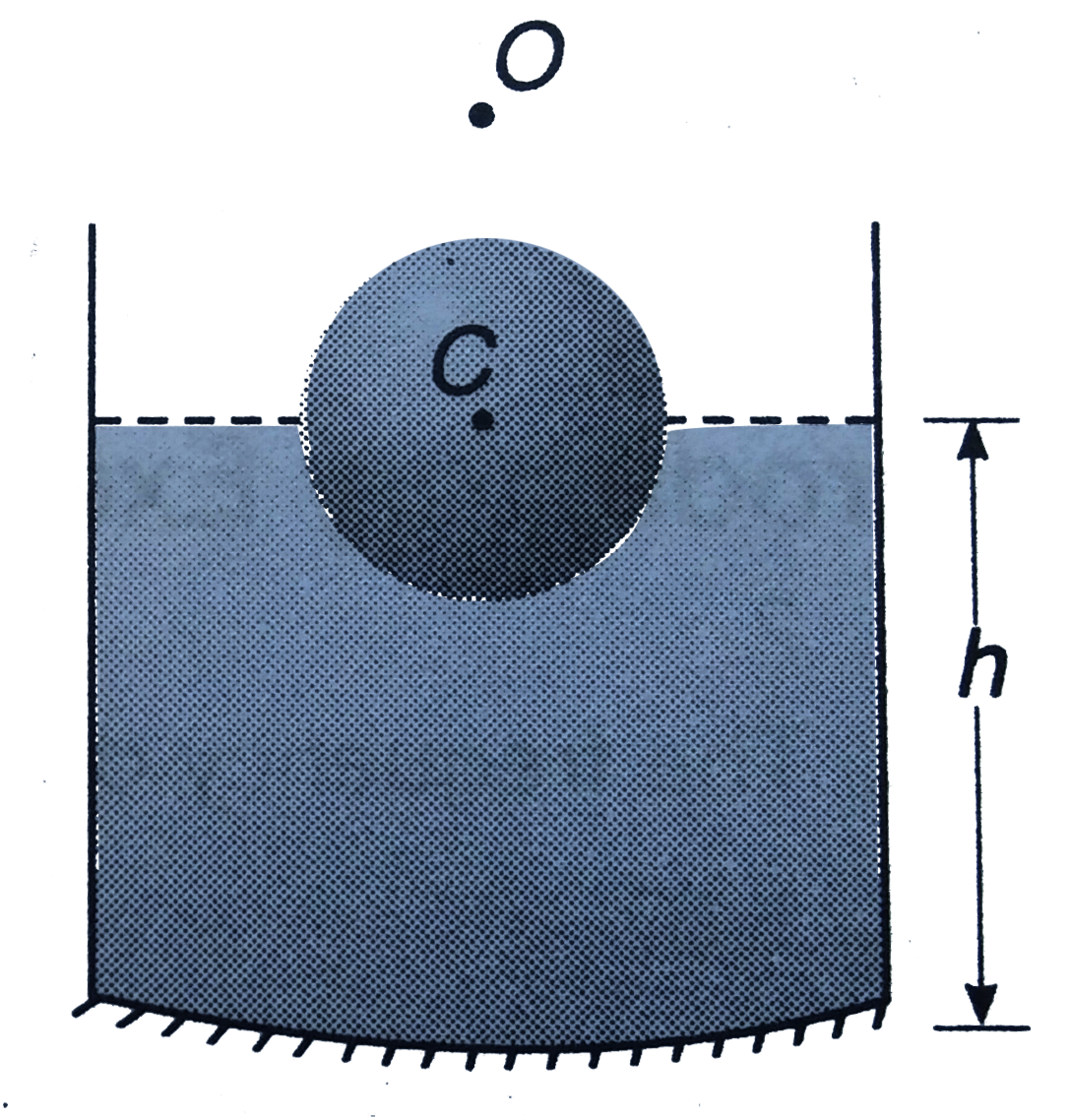
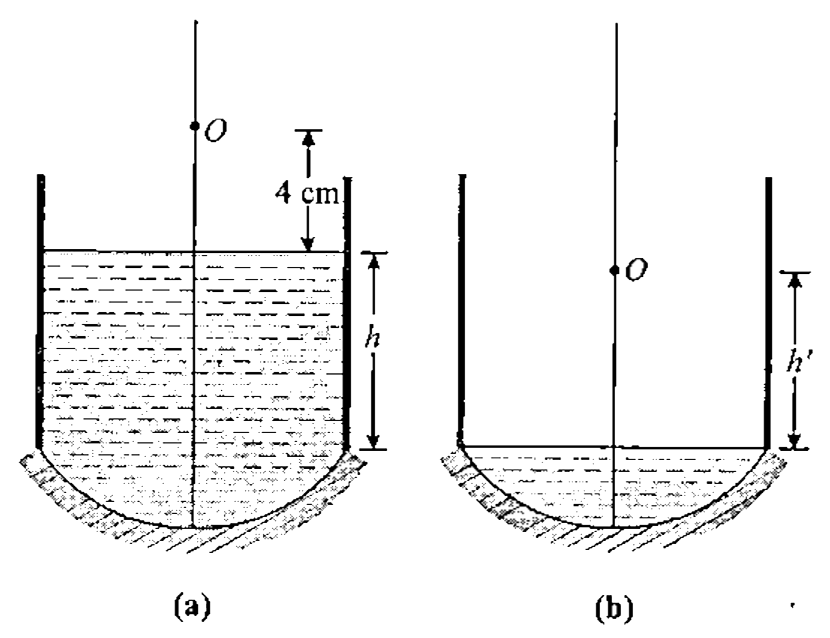
View SolutionA beaker is filled with water as shown in figure (a). The bottom surface of the beaker is a concave mirror of large radius of curvature and small aperture. The height of water is h=40cm. It is found that when an object is placed 4 cm above the water surface, the image coincides with the object. Now the water level h is reduced to zero but there will still be some water left in the concave part of the mirror as shown in figure (b). The new height of the object h' above the new water surface so that the image again coincides with the object, will be (Refractive index of water =4/3)
View SolutionA particle lies on the bottom of a tank T filled with water upto s height of 90cm. The medium above the surface of water is of R.I=1.2 above which there is mirror M. Beyond the mirror M the region contains air (μ=1). The distance of the image formed by the mirrro after reflection of the rays coming from P is ____ cm (w.r.t mirror).
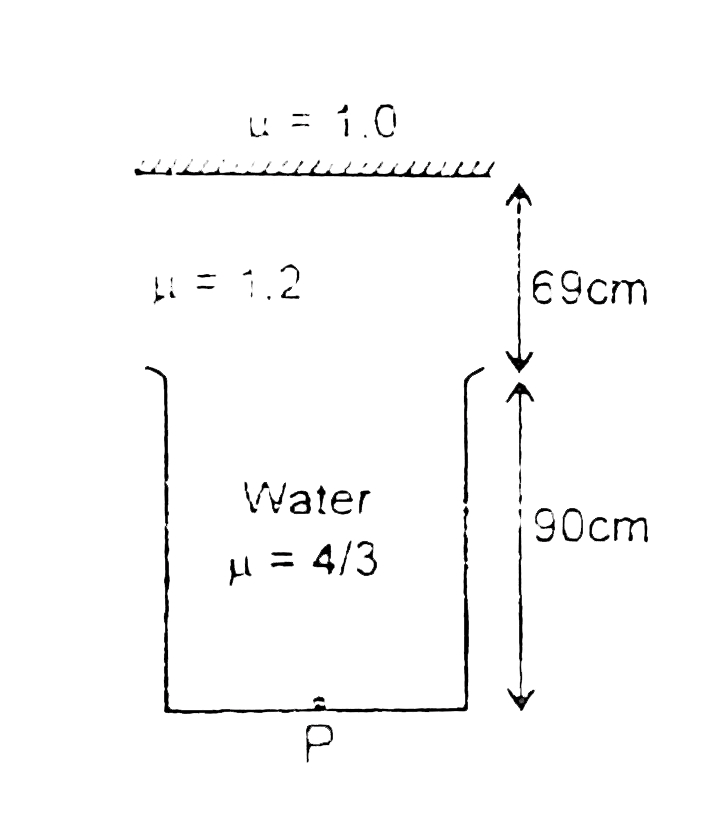 .
.
View Solution
