A conducting circular loop is in a perpendicular magnetic field of induction 10−2T If the radius of the loop starts shrinking at a uniform rate of 1 mm/s, then the e.m.f. induced in the loop at the instant when its radius is 10 cm will be
1 μ V
2 μ V
πμ V
2πμ V
To solve the problem, we need to calculate the induced electromotive force (e.m.f.) in a conducting circular loop that is shrinking in a magnetic field. We will use Faraday's law of electromagnetic induction, which states that the induced e.m.f. is equal to the rate of change of magnetic flux through the loop.
1. Identify the Given Values:
- Magnetic field induction, B=10−2T
- Rate of change of radius, drdt=−1mm/s=−1×10−3m/s (negative because the radius is decreasing)
- Radius at the instant of interest, r=10cm=0.1m
2. Calculate the Area of the Loop:
The area A of a circular loop is given by the formula:
A=πr2
Substituting the value of r:
A=π(0.1)2=π×0.01=0.01πm2
3. Determine the Rate of Change of Area:
To find the rate of change of area dAdt, we differentiate the area with respect to time:
dAdt=ddt(πr2)=π⋅2r⋅drdt
Substituting the known values:
dAdt=π⋅2⋅0.1⋅(−1×10−3)=−0.0002πm2/s
4. Calculate the Induced e.m.f.:
According to Faraday's law, the induced e.m.f. E is given by:
E=−BdAdt
Substituting the values:
E=−(10−2)(−0.0002π)=10−2×0.0002π=2×10−6πV
5. Convert to Microvolts:
Since 1μV=10−6V, we can express the result as:
E=2πμV
Final Answer:
The induced e.m.f. in the loop when its radius is 10 cm is:
E=2πμV
- Magnetic field induction, B=10−2T
- Rate of change of radius, drdt=−1mm/s=−1×10−3m/s (negative because the radius is decreasing)
- Radius at the instant of interest, r=10cm=0.1m
The area A of a circular loop is given by the formula:
A=πr2
Substituting the value of r:
A=π(0.1)2=π×0.01=0.01πm2
To find the rate of change of area dAdt, we differentiate the area with respect to time:
dAdt=ddt(πr2)=π⋅2r⋅drdt
Substituting the known values:
dAdt=π⋅2⋅0.1⋅(−1×10−3)=−0.0002πm2/s
According to Faraday's law, the induced e.m.f. E is given by:
E=−BdAdt
Substituting the values:
E=−(10−2)(−0.0002π)=10−2×0.0002π=2×10−6πV
Since 1μV=10−6V, we can express the result as:
E=2πμV
The induced e.m.f. in the loop when its radius is 10 cm is:
E=2πμV
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE - I (MAGNETIC FLUX, FARADAY.S LAW, LENZ.S LAW, AC GENERATOR)26videos
ELECTROMAGNETIC INDUCTION
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE - I (SELF AND MUTUAL INDUCTION)16videos
ELECTROMAGNETIC INDUCTION
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE-II32videos
ELECTROMAGNETIC INDUCTION
- BOOK - AAKASH SERIESCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - PROBLEMS (LEVEL-II)26videos
ELECTRIC FIELD AND POTENTIAL
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - EXERCISE -II22videos
ELECTROMAGNETIC WAVES
Similar Questions
A conducing circular loop is placed in a uniform magnetic field of indution B tesla with its plane normal to the field. Now, radius of the loop starts shrinking at the rate (dr/dt). Then the induced e.m.f. at the instant when the radius is r is:
View SolutionA conducting square loop is placed in a magnetic field B with its plane perpendicular to the field. Now the sides of the loop start shrinking at a constant rate α. the induced emf in the loop at an instant when its side is a is
View Solution
Knowledge Check
- Question 1 - Select One
A conducting circular loop is placed in a uniform magnetic field, B=0.025T with its plane perpendicular to the loop. The radius of the loop is made to shrink at a constant rate of 1mms−1. The induced emf when the radius is 2cm is
A2πμVBπμVCπ2μVD2μV
A conducting circular loop is placed is a uniform magnetic field B =0.20 T with its plane perpendicular to the field . Somehow, the radius of the loop starts shrinking at a constant rate of 1.0mms−1. Find the induced emf in the loop at an instant when the radius is 2 cm.
View SolutionA conducting circular loop is placed in a uniform magnetic field 0.04T with its plane perpendicular to the magnetic field. The radius of the loop starts shrinking at 2mm/sec . The induced emf in the loop when the radius is 2cm is:
(1.) 3.2 π μ V
(2.) 4.8 π μ V
(3.) 0.8 π μ V
(4.) 1.6 π μ VView SolutionRadius ol a circular luop placed in a perpendicular uniform magnetic field is increasing at a constant rate of roms1. If at any instant radius of the loop is r, then emf induced in the loop at that instant will be
View SolutionA conducting circualr loop is placed in a unifrom magentic field , B= 0.025 T with its plane perpendicular to the loop .The radius of the loop is made to shrink at a constant rate of 1 mms−1 .The induced emf when the radius is 2cm ,is
View SolutionA semi circular current loop is placed in an uniform magnetic field of 1 tesla as shown. If the radius of loop is 1 m, the magnetic force on the loop is
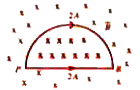 View Solution
View SolutionA circular loop is placed in magnetic field B=2t. Find the direction of induced current produced in the loop.
 View Solution
View SolutionA rectangular copper coil is placed in a uniform magnetic field of induction 40 mT with its plane perpendicular to the field. The area of the coil is shrinking at a constant rate of 0.5m2s−1. The emf induced in the coil is
View Solution

