A convergent lens with a focal length of f=10cm is cut into two halves that are then moved apart to a distance of d=0.5 mm (a double lens). Find the fringe width on screen at a distance of 60 cm behind the lens if a point sources of monochromatic light (λ=5000Å) is placed in front of the lens at a distance of a = 15cm from it.
The correct Answer is:A
To solve the problem step by step, we will follow the outlined procedure in the video transcript and add necessary calculations.
Step 1: Understand the Setup
We have a convergent lens with a focal length f=10cm that is cut into two halves and separated by a distance d=0.5mm=0.05cm. A point source of monochromatic light with a wavelength λ=5000Å=5000×10−10m=5×10−7m is placed at a distance a=15cm from the lens. We need to find the fringe width on a screen located D=60cm behind the lens.
Step 2: Find the Image Distance v
Using the lens formula:
1v−1u=1f
where u=−15cm (negative because the object is on the same side as the incoming light).
Substituting the values:
1v−1−15=110
This simplifies to:
1v+115=110
Now, finding a common denominator (which is 30):
230+230=330
Thus:
1v=330−230=130
So:
v=30cm
Step 3: Calculate the Effective Distance Between the Lens Halves
The distance between the two halves of the lens is d=0.05cm. Since the lens is cut into two halves, the distance between the two effective sources (the two halves of the lens) is d=0.05cm.
Step 4: Calculate the Total Distance to the Screen
The distance from the lens to the screen is given as D=60cm. The distance from the image formed to the screen is:
D′=D−v=60cm−30cm=30cm
Step 5: Calculate the Fringe Width
The formula for fringe width w is given by:
w=λD′d
Substituting the values:
w=5×10−7m×30×10−2m0.05×10−2m
Calculating this:
w=5×10−7×30×10−20.05×10−2=5×300.05×10−7=1500.05×10−7=3000×10−7=3×10−4m=0.3mm
Final Answer
The fringe width on the screen is 0.3mm.
We have a convergent lens with a focal length f=10cm that is cut into two halves and separated by a distance d=0.5mm=0.05cm. A point source of monochromatic light with a wavelength λ=5000Å=5000×10−10m=5×10−7m is placed at a distance a=15cm from the lens. We need to find the fringe width on a screen located D=60cm behind the lens.
Using the lens formula:
1v−1u=1f
where u=−15cm (negative because the object is on the same side as the incoming light).
1v−1−15=110
This simplifies to:
1v+115=110
Now, finding a common denominator (which is 30):
230+230=330
Thus:
1v=330−230=130
So:
v=30cm
The distance between the two halves of the lens is d=0.05cm. Since the lens is cut into two halves, the distance between the two effective sources (the two halves of the lens) is d=0.05cm.
The distance from the lens to the screen is given as D=60cm. The distance from the image formed to the screen is:
D′=D−v=60cm−30cm=30cm
The formula for fringe width w is given by:
w=λD′d
Substituting the values:
w=5×10−7m×30×10−2m0.05×10−2m
Calculating this:
w=5×10−7×30×10−20.05×10−2=5×300.05×10−7=1500.05×10−7=3000×10−7=3×10−4m=0.3mm
The fringe width on the screen is 0.3mm.
Topper's Solved these Questions
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 2 Single Correct
11 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - LEVEL 2 (single correct option)
1 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 1Subjective
22 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery
59 Videos
Similar Questions
A convex lens of focal length 10 cm is painted black at the middle portion as shown in figure. An object placed at a distance of 20 cm from the lens. Then
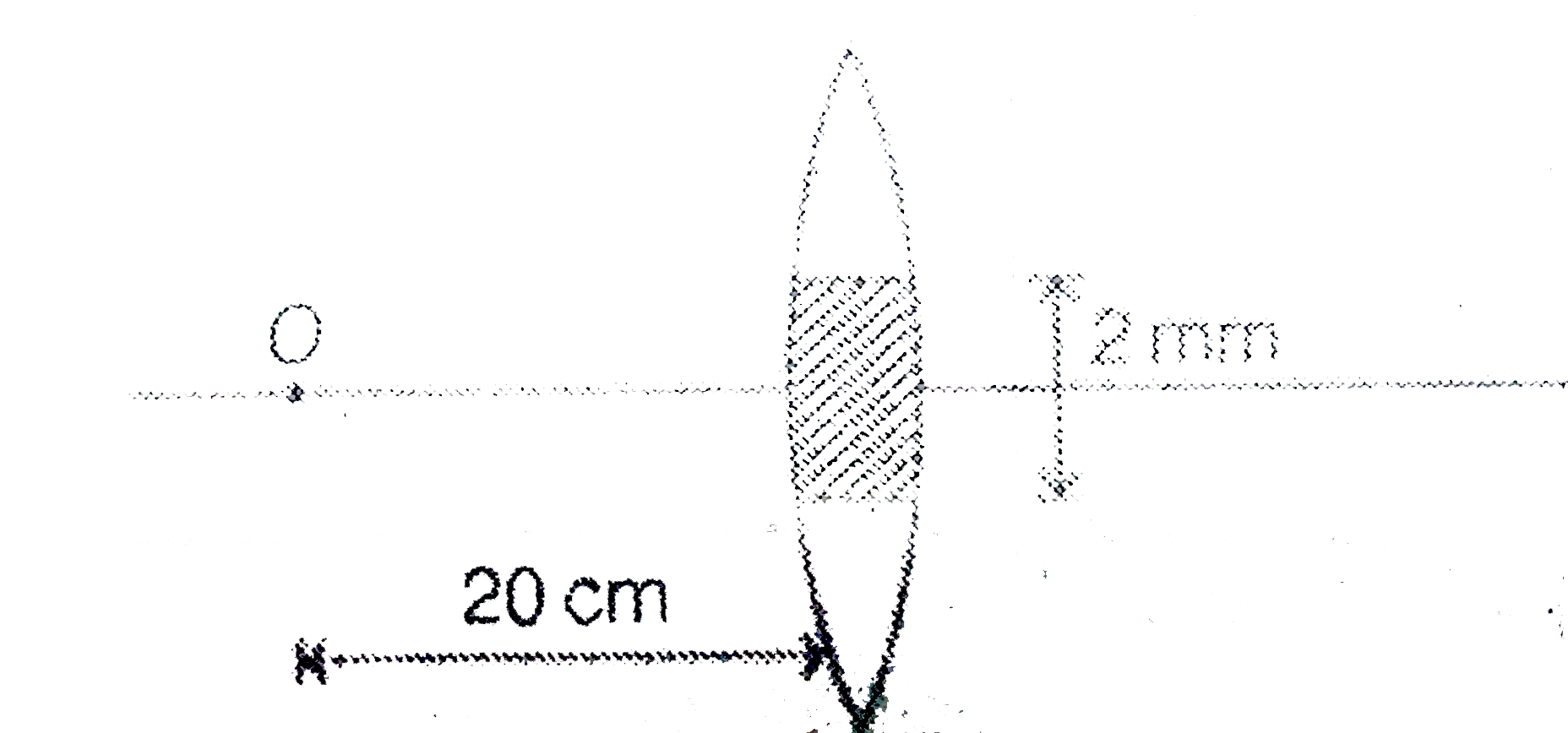
View SolutionA convex lens of focal length 20 cm is placed in front of a convex mirror of focal length 15 cm at a distance of 5 cm. An object of length 2 cm is placed perpendicular to the common axis at a distance of 20 cm from the lens
View Solution
Knowledge Check
A concave lens is placed in contact with a convex lens of focal length 25cm. The combination produces a real image at a distance of 80cm, when an object is at a distance of 40cm. What is the focal length of concave lens ?
A−400cmB−200cmC+400cmD+200cm
A lens with a focal length of 16cm produces a sharp image of an object in two positions, which are 60cm apart. Find the distance from the object to the screen.
View SolutionA convex lens of focal length 15cm is split into two halves and the two halves are placed at a separation of 120cm. Between, the two halves of convex lens a plane mirror is placed horizontal and at a distance of 4mm below the principal axis of the lens halves. An object of length 2mm is placed at a distance of 20cm from one half lens as shown in figure.

Find the position and size of the final image.
Trace the path of rays forming the image.
View SolutionA thin converging lens of focal length f = 25 cm forms the image of an object on a screen placed at a distance of 75 cm from the lens. Now the screen in moved closer to the lens by a distance of 25 cm. The distance through which the object has to be shifted so that its image on the screen is sharp again is
View SolutionA convex lens has a focal length of 10 cm. Find the location and nature of the image if a point object is placed on the principal axis at a distance of (a) 9.8 cm, (b) 10.2 cm from the lens.
View SolutionAn optical system consists of a thin convex lens of focal length 30cm and a plane mirror placed 15cm behind the lens. An object is placed 15cm in front of the lens. The distance of the final image from the object is
View SolutionA concave lens has focal length of 15 cm. At what distance should an object from the lens be placed so that it forms an image at 10 cm from the lens ? Also, find the magnification of the lens.
View SolutionAn equi-convex lens of focal length F in air is is cut into two halves along the plane perpendicular to the optic axis. One of the halves is placed between a fixed object and a screen separated by distance of 90 cm . Two images are formed on the screen for two different positions of the lens with magnification 2 and 1/2 respectively. Find the value of F . what would be the value of the focal length of the equiconvex lens if the lens is immersed in water ? Refractive index of the material of the lens is 1.5 and that of water is μw=4/3.
View Solution
