A cookie jar is moving up a 40∘ incline. At a point 45 cm from the bottom of the incline ( measured along the incline ) ,the jar has a speed of 1.4 m/s. The coefficient of kinetic friction between jar and incline is 0.15 . (a) How much farther up the incline will the jar move ? (b) How fast will it be going when it has slid back to the bottom of the incline ? (c) Do the answers to parts (a) and (b) increase, decrease, or remain the same if we decrease the coefficient of kinetic friction ( but do not change the given speed or location ) ?
The correct Answer is:(a) 0.13 m ; (b) 2.5 m/s ; (c) In part (a) it is clear that d increases if μk decreases and in part (b), the factor itself increases in value.
To solve the problem step by step, we will break it down into parts (a), (b), and (c) as outlined in the question.
Part (a): How much farther up the incline will the jar move?
1. Identify the Forces Acting on the Jar:
- The gravitational force acting down the incline: Fg=mgsinθ
- The frictional force acting down the incline: Ff=μmgcosθ
- The total deceleration a when the jar is moving up is given by:
a=gsinθ+μgcosθ
2. Calculate the Acceleration:
- Given θ=40∘, μ=0.15, and g=9.81m/s2:
a=gsin(40∘)+μgcos(40∘)
- Calculate sin(40∘) and cos(40∘):
sin(40∘)≈0.6428,cos(40∘)≈0.7660
- Substitute these values into the acceleration equation:
a=9.81×0.6428+0.15×9.81×0.7660
a≈6.303+1.125≈7.428m/s2
3. Use the Kinematic Equation:
- The initial speed u=1.4m/s and final speed v=0m/s when the jar stops.
- Using the equation v2=u2+2as:
0=(1.4)2−2(7.428)s
0=1.96−14.856s
14.856s=1.96⇒s=1.9614.856≈0.132m≈13.2cm
4. Total Distance Up the Incline:
- The jar moves an additional 13.2cm up the incline.
Part (b): How fast will it be going when it has slid back to the bottom of the incline?
1. Calculate the Total Distance Down:
- The total distance down is the distance it initially moved up (45 cm) plus the distance it moved up before stopping (13.2 cm):
Total distance down=0.45m+0.132m=0.582m
2. Calculate the Acceleration Going Down:
- When the jar slides down, the acceleration is:
a′=gsinθ−μgcosθ
- Substitute the values:
a′=9.81×0.6428−0.15×9.81×0.7660
a′≈6.303−1.125≈5.178m/s2
3. Use the Kinematic Equation Again:
- Initial speed u=0m/s at the top, final speed v at the bottom:
v2=u2+2a′s
v2=0+2(5.178)(0.582)
v2=6.048⇒v=√6.048≈2.46m/s
Part (c): Effect of Decreasing the Coefficient of Kinetic Friction
1. Distance Up the Incline:
- If the coefficient of kinetic friction μ decreases, the deceleration a will decrease, leading to a greater distance traveled up the incline.
2. Velocity at the Bottom:
- Similarly, if μ decreases, the acceleration a′ when sliding down will increase, leading to a higher final velocity when the jar reaches the bottom.
Summary of Answers:
- (a) The jar will move approximately 13.2 cm farther up the incline.
- (b) The speed when it slides back to the bottom will be approximately 2.46 m/s.
- (c) Both the distance traveled up the incline and the final velocity at the bottom will increase if the coefficient of kinetic friction is decreased.
- The gravitational force acting down the incline: Fg=mgsinθ
- The frictional force acting down the incline: Ff=μmgcosθ
- The total deceleration a when the jar is moving up is given by:
a=gsinθ+μgcosθ
- Given θ=40∘, μ=0.15, and g=9.81m/s2:
a=gsin(40∘)+μgcos(40∘)
- Calculate sin(40∘) and cos(40∘):
sin(40∘)≈0.6428,cos(40∘)≈0.7660
- Substitute these values into the acceleration equation:
a=9.81×0.6428+0.15×9.81×0.7660
a≈6.303+1.125≈7.428m/s2
- The initial speed u=1.4m/s and final speed v=0m/s when the jar stops.
- Using the equation v2=u2+2as:
0=(1.4)2−2(7.428)s
0=1.96−14.856s
14.856s=1.96⇒s=1.9614.856≈0.132m≈13.2cm
- The jar moves an additional 13.2cm up the incline.
- The total distance down is the distance it initially moved up (45 cm) plus the distance it moved up before stopping (13.2 cm):
Total distance down=0.45m+0.132m=0.582m
- When the jar slides down, the acceleration is:
a′=gsinθ−μgcosθ
- Substitute the values:
a′=9.81×0.6428−0.15×9.81×0.7660
a′≈6.303−1.125≈5.178m/s2
- Initial speed u=0m/s at the top, final speed v at the bottom:
v2=u2+2a′s
v2=0+2(5.178)(0.582)
v2=6.048⇒v=√6.048≈2.46m/s
- If the coefficient of kinetic friction μ decreases, the deceleration a will decrease, leading to a greater distance traveled up the incline.
- Similarly, if μ decreases, the acceleration a′ when sliding down will increase, leading to a higher final velocity when the jar reaches the bottom.
- (a) The jar will move approximately 13.2 cm farther up the incline.
- (b) The speed when it slides back to the bottom will be approximately 2.46 m/s.
- (c) Both the distance traveled up the incline and the final velocity at the bottom will increase if the coefficient of kinetic friction is decreased.
Topper's Solved these Questions
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PRACTICE QUESTIONS (Single Correct Choice Type)
59 Videos
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PRACTICE QUESTIONS (More than one choice correct type)
10 Videos
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - CHECKPOINT
6 Videos
- WAVES-IBOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Practice Questions (Integer Type)
4 Videos
Similar Questions
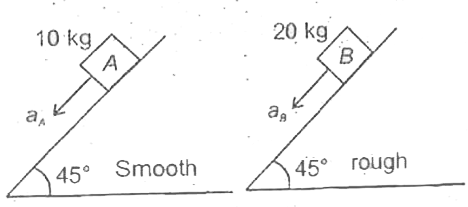
The ratio of acceleration of blocks A placed on smooth incline with block B placed on rough incline is 2:1. The coefficient of kinetic friction between block B and incline is
View SolutionBlock of mass 10 kg is moving on inclined plane with constant velocity 10 m/s. The coedfficient of kinetic friction between incline plane and block is :-

View Solution
Knowledge Check
A block is placed on an inclined plane. The angle of inclination of the plane is such that the block slides down the plane at a constant speed. The coefficient of kinetic friction is
AsinθBcosθCcotθDtanθA block sliding down on a rough 45∘ inclined plane has half the velocity it would have been, the inclined plane is smooth. The coefficient of sliding friction between the block and the inclined plane is
A14B34C12√2D1√2A block of mass m sliding down an inclined at constant speed is initial at a height h shown the ground as shown in the figure above . The coefficient of kinetic friction between the mass and the inclined is μ . If the mass constinues to slide down the inclined at a constant speed how much energy is displaced by friction by the time the mass reaches the bottom of the incline?
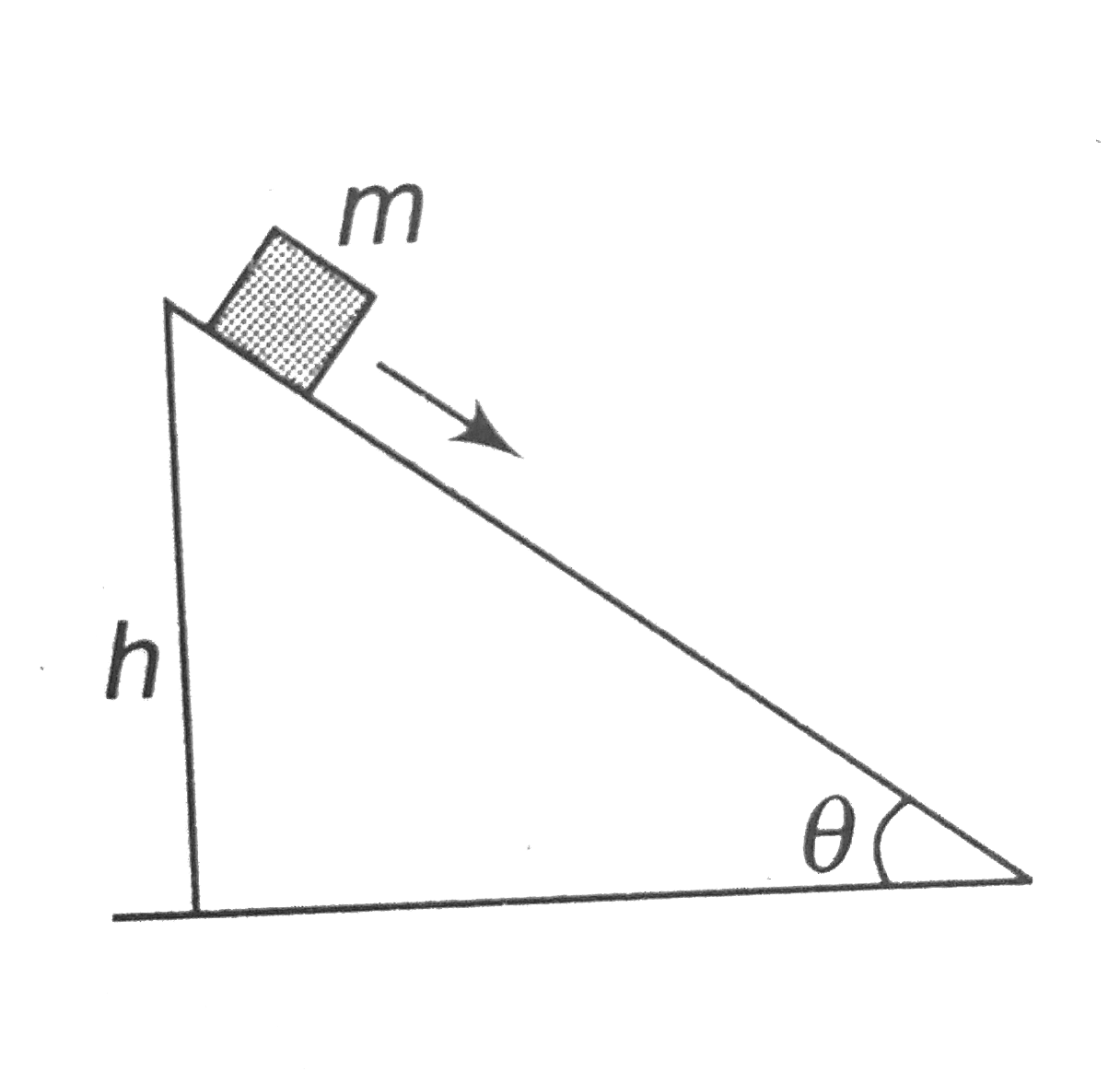 Amgh/θBmghCμmgh/sinθDmghsinθ
Amgh/θBmghCμmgh/sinθDmghsinθ
A block of mass m moves with constant speed down the inclined plane of inclination θ. Find the coefficient of kinetic friction.
View SolutionA 4.0 kg bundle starts up a 30∘ incline with 150 J of kinetic energy. How far will it slide up the incline if the coefficient of kinetic friction between bundle and incline is 0.36 ?
View SolutionProjectile on an incline plane (up and down the incline)
View SolutionProjectile on an incline plane (up and down the incline)
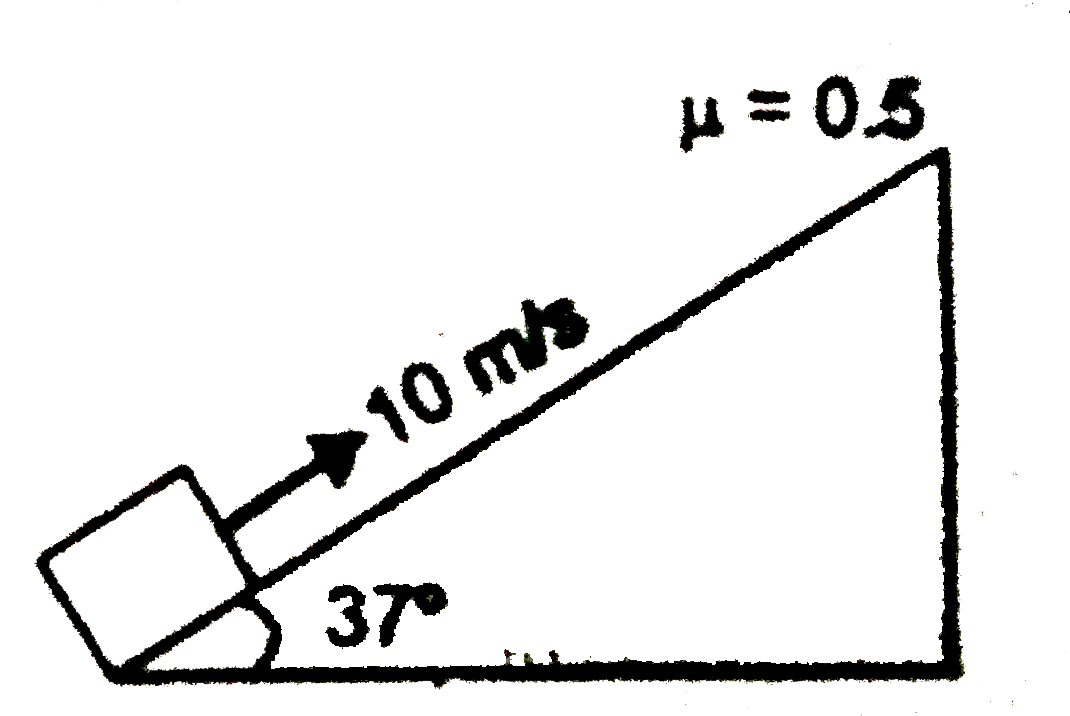
View SolutionA block is given velocity 10 m/s along the fixed inclined as shown in figure from the bottom of the inclined plane. Find the total distance travelled along the inclined plane. If the coefficient of friction is equal to 0.5
View Solution
