A copper ball of diameter d was placed in an evacuated vessel whose walls are kept at the absolute zero temperature. The initial temperature of the ball is t0. Assuming the surface of the ball to be absolutely black, find how soon its temperature decreases η times. Take specific heat of copper c, density of copper ρ and emissivity e.
To solve the problem, we need to determine how long it takes for the temperature of a copper ball to decrease to T0η when placed in an evacuated vessel at absolute zero temperature. We will use the principles of heat transfer through radiation.
1. Identify the Parameters:
- Let the diameter of the copper ball be d.
- The radius r of the ball is d2.
- The initial temperature of the ball is T0.
- The final temperature we want to find the time for is T0η.
- The specific heat capacity of copper is c.
- The density of copper is ρ.
- The emissivity of the surface is e.
2. Calculate the Surface Area:
The surface area A of the sphere (copper ball) is given by:
A=4πr2=4π(d2)2=πd2
3. Determine the Power Radiated:
The power P radiated by the ball can be expressed using the Stefan-Boltzmann law:
P=eσAT4=eσ(πd2)T4
where σ is the Stefan-Boltzmann constant.
4. Relate Power to Heat Loss:
The rate of heat loss dqdt is equal to the power radiated:
dqdt=−P=−eσπd2T4
5. Express Heat Loss in Terms of Temperature Change:
The heat lost by the ball can also be expressed in terms of its mass and specific heat:
dq=mcdT
where m is the mass of the ball. The mass m can be calculated as:
m=ρV=ρ(43πr3)=ρ(43π(d2)3)=ρπd36
Thus,
dq=ρπd36cdT
6. Set Up the Differential Equation:
Equating the two expressions for dq:
ρπd36cdT=−eσπd2T4dt
Dividing through by π and rearranging gives:
dTdt=−6eσρcdT4
7. Integrate the Equation:
We need to integrate this equation from T0 to T0η:
∫T0ηT01T4dT=−6eσρcd∫t0dt
The left-hand side integrates to:
−13(1T3)T0ηT0=−13⎛⎜
⎜⎝1(T0η)3−1T30⎞⎟
⎟⎠
Simplifying gives:
−13(η3−1T30)=−6eσρcdt
8. Solve for Time t:
Rearranging to solve for t:
t=ρcd18eσ(η3−1T30)
Final Result:
The time t it takes for the temperature of the copper ball to decrease to T0η is given by:
t=ρcd18eσ(η3−1T30)
- Let the diameter of the copper ball be d.
- The radius r of the ball is d2.
- The initial temperature of the ball is T0.
- The final temperature we want to find the time for is T0η.
- The specific heat capacity of copper is c.
- The density of copper is ρ.
- The emissivity of the surface is e.
The surface area A of the sphere (copper ball) is given by:
A=4πr2=4π(d2)2=πd2
The power P radiated by the ball can be expressed using the Stefan-Boltzmann law:
P=eσAT4=eσ(πd2)T4
where σ is the Stefan-Boltzmann constant.
The rate of heat loss dqdt is equal to the power radiated:
dqdt=−P=−eσπd2T4
The heat lost by the ball can also be expressed in terms of its mass and specific heat:
dq=mcdT
where m is the mass of the ball. The mass m can be calculated as:
m=ρV=ρ(43πr3)=ρ(43π(d2)3)=ρπd36
Thus,
dq=ρπd36cdT
Equating the two expressions for dq:
ρπd36cdT=−eσπd2T4dt
Dividing through by π and rearranging gives:
dTdt=−6eσρcdT4
We need to integrate this equation from T0 to T0η:
∫T0ηT01T4dT=−6eσρcd∫t0dt
The left-hand side integrates to:
−13(1T3)T0ηT0=−13⎛⎜
⎜⎝1(T0η)3−1T30⎞⎟
⎟⎠
Simplifying gives:
−13(η3−1T30)=−6eσρcdt
Rearranging to solve for t:
t=ρcd18eσ(η3−1T30)
The time t it takes for the temperature of the copper ball to decrease to T0η is given by:
t=ρcd18eσ(η3−1T30)
Topper's Solved these Questions
- HEAT TRANSFER BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Practice Exercise 4.3
5 Videos
- HEAT TRANSFER BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Practice Exercise 4.4
5 Videos
- HEAT TRANSFER BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Practice Exercise 4.1
11 Videos
- HEAT AND THERMAL EXPANSIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT AND THERMAL EXPANSIONEXERCISE - UNSOLVED NUMRICAL PROBLEMS FOR PREPARATION OF NSEP, INPhO & IPhO
82 Videos
- Kinetic Theory of Gases and Gas LawsBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - Kinetic Theory of Gases and Gas LawsEXERCISE - Unsolved Numerical Problems for Preparation of NSEP, INPhO & IPhO
64 Videos
Similar Questions
A copper ball of diameter d=1.2cm was placed in an evacuated vessel whose walls are kept at the absolute zero temperature. The initial temperatures of the ball is T0=300K. Assuming the surface of the ball to be absolutely balck, find how soon its temperature decreases η=2.0 times.
View SolutionA spherical ball of surface area 2×10−3m2 is suspended in a room at temperature 330 K. If the temperature of the ball is 200∘C, find the net rate of loss of heat from the ball if it behaves like a black body.
View Solution
Knowledge Check
A copper ball of mass 100 gm is at a temperature T. It is dropped in a copper calorimeter of mass 100 gm, filled with 170 gm of water at room temperature. Subsequently, the temperature of the system is found to be 75∘C . T is given by : (Given : room temperature = 30∘C, specific heat of copper =0.1cal/gm∘C)
A1250∘CB825∘CC800∘CD885∘CA metal ball of specific gravity 4.5 and specific heat 0.1cal/gm−∘C is placed on a large slab of ice at 0∘C. Half of the ball sinks in the ice. The initial temperature of the ball is:- (Latent heat capacity of ice =80cal/g, specific gravity of ice =0.9)
A100∘CB90∘CC80∘CD70∘C
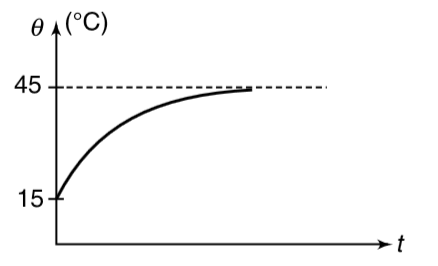
A metal ball of mass 1.0 kg is kept in a room at 15∘C. It is heated using a heater. The heater supplies heat to the ball at a constant rate of 24 W. The temperature of the ball rises as shown in the graph. Assume that the rate of heat loss from the surface of the ball to the surrounding is proportional to the temperature difference between the ball and the surrounding. Calculate the rate of heat loss from the ball when it was at temperature of 20∘C.
View SolutionIn a laboratory experiment to measure the specific heat capacity of copper, 0.02 kg of water at 70∘C was poured into a copper calorimeter with a stirrer of mass 0.16 kg initially at 15∘C. After stirring the final temperature reached to 45∘C.
Assuming that heat released by water is entirely used to raise the temperature of calorimeter 15∘C to 45∘C, calculate the specific heat capacity of copper. (Specific heat capacity of water = 4200Jkg−1∘C−1.
View SolutionA solid aluminium sphere and a solid copper sphere of twice the radius are heated to the same temperature and are allowed to cool under identical surrounding temperatures. Assume that the emissivity of both the spheres is the same. Find ratio of (a) the rate of heat loss from the aluminium sphere to the rate of all of temperature of the copper sphere. The specific heat capacity of aluminium =900Jkg−1^(@)C^(-1).andtˆofcopper=390Jkg^(-1)^(∘)C−1 . The density of copper =3.4 times the correct wattage.
View SolutionOne mode of an ideal monatomic gas is kept in a rigid vessel. The vessel is kept inside a steam chamber whose temperature is 97∘C . Initially, the temperature of the gas is 5.0∘C . The walls of the vessel have an inner surface of area 800cm2 and thickness 1.0cm If the temperature of the gas increases to 9.0∘C in 0.5 second, find the thermal conductivity of the material of the walls.
View SolutionConside a cubical vessel of edge a having a small hole in one of its walls is r. At time t=0 , it contains air at atmospheric pressure paandtemperatureT_(0).Thetemperatureofthesurroud∈gairisT_(a)(gtT_(0).F∈dtheamountofthegas(∈mo≤s)∈thevesselattimet.TakeC_(v)ofair→be5R/2.
View SolutionA solid aluminium sphere and a solid copper sphere of twice the radius are heated to the same temperature and are allowed to cool under identical surrounding temperature. Assume that the emissivity of both the spheres is the same. Find the ratio of
(a) the rate of heat from the aluminium sphere to the rate of heat loss from the copper sphere and
(b) the rate of fall of temperature of the the aluminium sphere to the rate of fall temperature of teh copper sphere. The specific heat capacity of aluminium =900J/kg−∘C and that of copper =390J/kg−∘C. The density of copper is 3.4 times the density of aluminium.
View Solution
