Conside a cubical vessel of edge a having a small hole in one of its walls is r. At time t=0 , it contains air at atmospheric pressure paandtemperatureT_(0).Thetemperatureofthesurroud∈gairisT_(a)(gtT_(0).F∈dtheamountofthegas(∈mo≤s)∈thevesselattimet.TakeC_(v)ofair→be5R/2.
As the gas can leak out of the hole, the pressure inside the vessel will be equal to the atmospheric pressure Pa . Let n be the amount of the gas (moles) in the vessel at time t. Suppose an amount DeltaQ of heat is given to the gas in time dt. Its temperature increases by dT where
ΔQ=nCpdT . If the temperature of the gas is T at time t. we have ΔQdt=Ta−Tr . or, (cpr)ndT=(TA−(T)dt . We have, paa3=nRT . or, ndt+Tdn=0 . or, ndT=−Tdn . Also, T=paa3nR . Using (ii) and (iii) in (i), −CprPaa3nRdn=(Ta−paa3nR)dt . or, dnnR(Ta−paa3nR)=−dtCprpaa3 . or, ∫nondnnRTa−paa3=−∫t0dtCprpaa3 . Where no=paa3RT0 . is the initial amount of the gas in the vessel . Thus, 1RTaln(nRt_(a)-p_(a)a^(3))/(n_(0)RT_(a)-p_(a)a^(3))=-(t)/(C_(p)rp_(a)a^(3)).or,nRT_(a)-p_(a)a^(3)=(n_(0)RT_(a)-p_(a)a^(3))e-^RTacprpaa3t . Writing n0=(paa3RT0 and C_(p)=C_(v)+R=(7R)/(2),n=(p_(a)a^(3))/(RT_(a))[1+(T_(a)/(T_(0))-1)e-^2Ta7rpaa3t] .
Topper's Solved these Questions
- HEAT TRANSFERBOOK - HC VERMACHAPTER - HEAT TRANSFEREXERCISE - Short Answer
11 Videos
- HEAT TRANSFERBOOK - HC VERMACHAPTER - HEAT TRANSFEREXERCISE - Objective 1
10 Videos
- HEAT TRANSFERBOOK - HC VERMACHAPTER - HEAT TRANSFEREXERCISE - EXERCIESE
1 Videos
- HEAT AND TEMPERATUREBOOK - HC VERMACHAPTER - HEAT AND TEMPERATUREEXERCISE - Exercise
4 Videos
- INTRODUCTION TO PHYSICSBOOK - HC VERMACHAPTER - INTRODUCTION TO PHYSICSEXERCISE - Exercises
19 Videos
Similar Questions
A container having 3 mole of gas occupies 60 litre at pressure P and temperature T if 0.2 mole of gas are introduced at same P and T Find the change in volume .
View SolutionTwo closed vessels of equal volume contain air at P0 pressure, T0 temperature and are connected through a narrow tube, If one of the vessels is now maintained at T0 and other at T, what will be the pressure in the vessels?
View Solution
Knowledge Check
Two idential container joined by a small pipe initially contain the same gas at pressure p0 and absolute temperature T0. One container is now maintained at the same temperature while the other is heated to 2T0. The common pressure of the gas
A32p0B43p0C5p0D2p0For an ideal gas number of moles per litre in terms of its pressure P gas contant R and temperature T is .
APT/RBPRTCP/RTDRT/PTwo closed vessels of equal volume containing air at pressure P1 and temperature T1 are connected to each other through a narrow tube. If the temperature in one of the vessels is now maintained at T1 and that in the other at T2, what will be the pressure in the vessels?
A2P1T1T1+T2BT12P1T2C2P1T2T1+T2D2P1T1+T2
A spherical container made of non conducting wall has a small orifice in it. Initially air is filled in it at atmospheric pressure (P0) and atmospheric temperature (T0). Using a small heater, heat is slowly supplied to the air inside the container at a constant rate of H J/s. Assuming air to be an ideal diatomic gas find its temperature as a function of time inside the container.
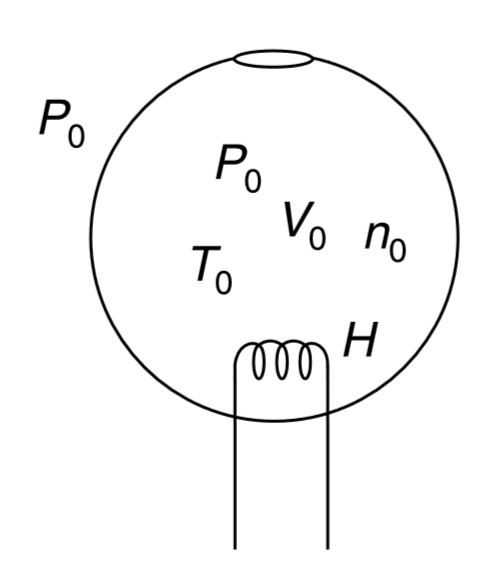
View SolutionTwo closed vessels of equal volume containing air at pressure P1 and temperature T1 are connected to each other through a narrow tube. If the temperature in one of the vessels is now maintained at T1 and that in the other at T2, what will be the pressure in the vessels?
View SolutionA vessel contains water at 100∘ C. The temperature falls to 80∘ C in time T1 and to 60∘ C in further time T2 , then
View SolutionFor an ideal gas, number of moles per litre in terms of its pressure P, gas constant R and temperature T is
View SolutionThe air tight and smooth piston of a cylindrical vessel are connected with a string as shown. Initially pressure and temperature of the gas are P0 and T0. The atmospheric pressure is also P0. At a later time, tension in the string is 38P0A where A is cthe cross-sectional are of the cylinder. at this time, the temperature of the gas has become.

View Solution
