A cotton reel of mass m, radius R and moment of inertia I is kept on a smooth horizontal surface. If the string is pulled horizontally by a force F, find the (i) acceleration of CM, (ii) angular acceleration of the cotton reel.

a. The net force acting on the cotton reel is
F=maC

or aC=Fm
b. the net torque about the CM is τC(=FR)=Iα
(as torques produced by mg and N about C are zero as they pass through the CM).
Then α=FRI
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Subjective
13 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Single Correct
97 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.3
15 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
Similar Questions
A cotton reel of mass m and moment of inertia I is kept at rest on as smooth horizontal surface. The reel has inner and other radius r and R respectively. A horizontal force F starts actings as shown in figure. Find the

a. acceleration of the centre of mass of reel.
b. angular acceleration of the reel
c. net acceleration of point of contact.
View SolutionTwo blocks A and B of masses m and M are attached with ideal string and pulley, and placed on smooth horizontal surface. Force F is applied horizontally as shown in figure. Find the ratio of the acceleration of A to that of B.

View Solution
Knowledge Check
A solid sphere of radius R is placed on a smooth horizontal surface. A horizontal force F is applied at height h from the lowest point. For the maximum acceleration of the centre of mass
Ah=RBh=2RCh=0Dthe acceleration will be same whatever h may beThe acceleration down the plane of spherical body of mass m radius R and moment of inertia I having inclination θ to the horizontal is
Agsinθ1+12/R2Bgsinθ1+I/R2Cgsinθ1+I/MR2DgsinθMR2+1
A uniform sphere is placed on a smooth horizontal surface and a horizontal force F is applied on it at a distance h above the surface. The acceleration of the centre :
View SolutionA uniform disc of mass m, radius R is placed on a smooth horizontal surface. If we apply a horizontal force F at P as shown in the figure. If F=4N,m=.1kg,R=1m and r=12m then, find the:
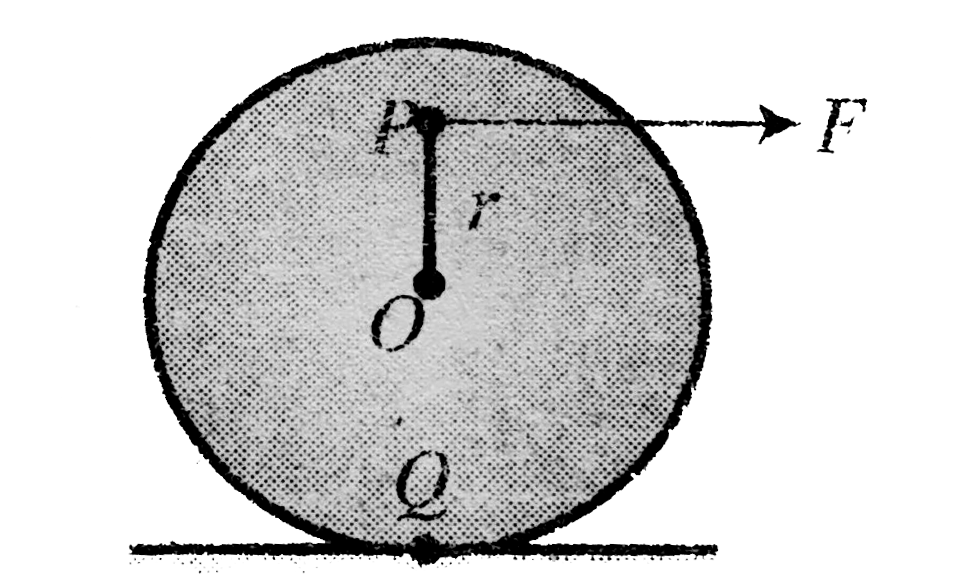
angular acceleration of the disc. (rads−1)
View SolutionA wheel of radius 20 cm and moment of inertia 1 kgm2 can rotate about its centre.A string is wrapped over its rim and is pulled by a force 'F' tangential to the rim of wheel.If angular acceleration produced is 2 rad/ s2 then the value of force 'F' is
View SolutionThree blocks of masses m1=10kg,m2=20kg,m3=30kg are connected by strings on smooth horizontal surface and pulled by a force of 60 N. Find the acceleration of the system and tensions in the string.

View SolutionConsider a disc of mass m and radius R placed on a rough plank of mass M which is turn is place on a smooth horizontal surface. Now plank is pulled by a force F and disc starts to roll on the plank.
If there is no friction any where then find
(a) Fricition force acting on the disc
(b) Angular acceleration of the disc

View SolutionFor the arrangement shown in the figure,blocks A and B are placed on the smooth horizontal surface.The free end P of the thread is being pulled by a constant force "F=1N" .Find the acceleration of free end P.
View Solution
