A cricket ball thrown across a field is a heights and from the point of projection at time and respectively after the throw. The ball is caught by a fielder at the same height as that of projection. The time of flight of the ball in this journey is
None of these
The correct Answer is:C
For vertically moment,
(for
........(i)
(for
........(ii)
On dividing Eq. (i) by Eq. (ii), we get
The time of flight of the ball,
[from Eq.(i)]
Topper's Solved these Questions
Similar Questions
A ball is projected vertically up such that it passes thorugh a fixes point after a time t0 and t2 respectively. Find
a. The height at which the point is located with respect to the point of projeciton
b. The speed of projection of the ball.
c. The velocity the ball at the time of passing through point P.
d. (i) The maximum height reached by the balll relative to the point of projection A (ii) maximum height reached by the ball relative to point P under consideration.
e. The average speed and average velocity of the ball during the motion from A to P for the time t1 and t2 respectively.
 .
.
View SolutionA tennis ball is thrown from a height h above the ground.If the coefficient of restitution is e,what height will the ball achieve after the third collision? "
View Solution
Knowledge Check
A ball is thrown upwards with a speed u from a height h above the ground.The time taken by the ball to hit the ground is
A√2h/gB√8h/gC√u2+2ghgDug+√2hgv20
A4:1B3:1C1:4D1:3A ball is thrown upwards from the top of an incline with angle of projection θ with the vertical as shown. Take θ=60∘ and g=10m/s2 . The ball lands exactly at the foot of the incline.
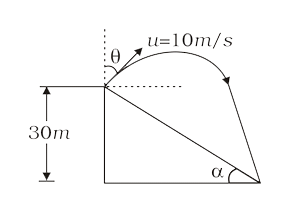
The time of flight of the ball is:At=√3sBt = 4 sCt = 3 sDt = 6 s
.A ball is projected upwards from a height h above the surface of the earth with velocity v .The time at which the ball strikes the ground is
View SolutionA ball is projected upwards from a height h above the surface of the earth with velocity v. The time at which the ball strikes the ground is
View SolutionA ball of mass m1 and another ball of mass m2 are dropped from equal height. If the time taken by the balls are t1 and t2, respectively, then
View SolutionTwo balls are dropped from heights h and 2h respectively. The ratio of time taken by these balls to reach the earth is
View SolutionA body is projected verticallt upwards. If t1 and t2 be the times at which it is at a height h above the point of projection while ascending and descending respectively, then:
View Solution
