A cubical block of glass, refractive index 1.5, has a spherical cavity of radius r=9cm inside it as shown in figure . A luminous point object O is at a distance of 18cm from the cube. What is the apparent position of O as seen from A?
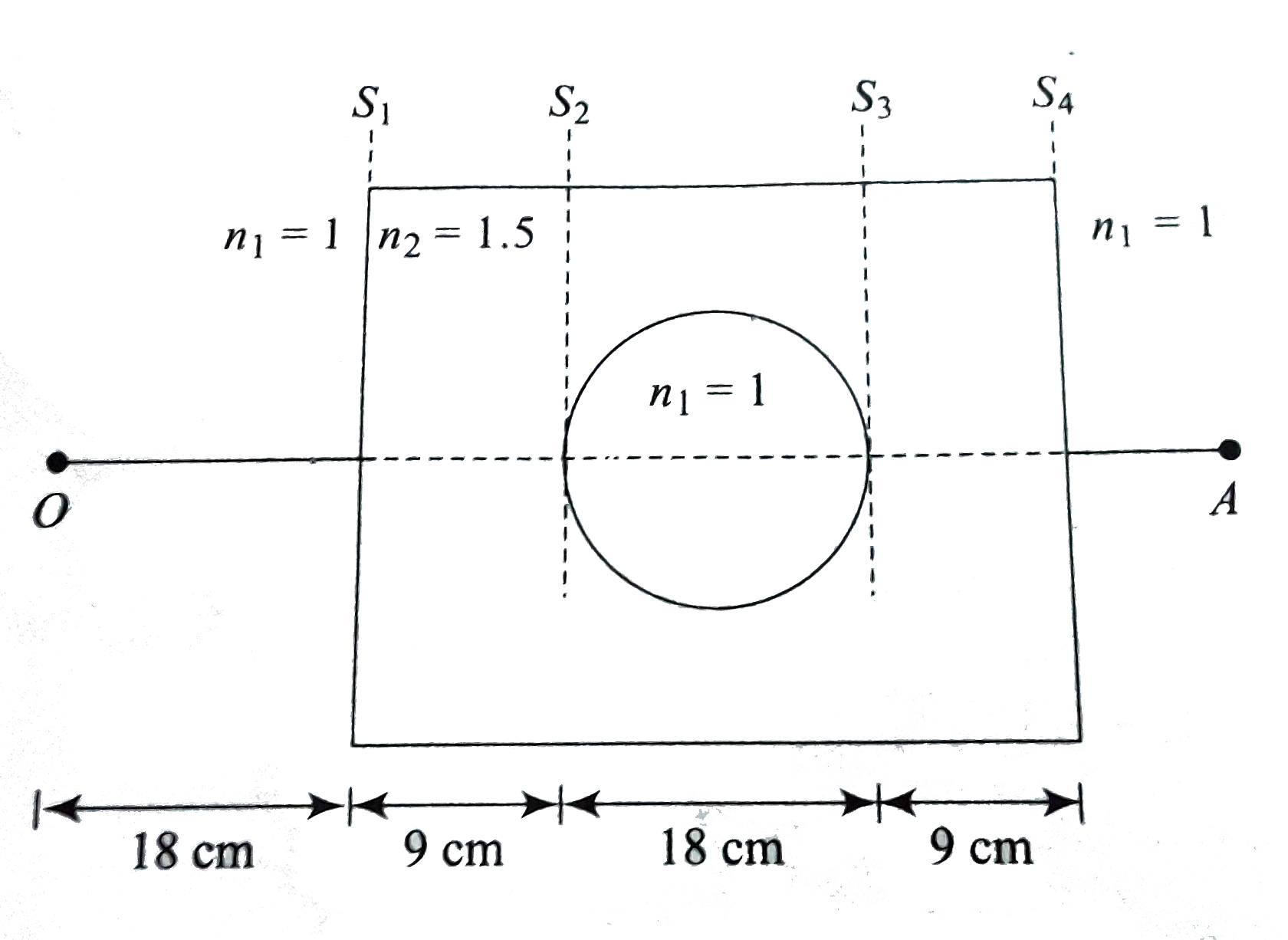
17cm, left of S4
25cm, right of S4
13cm, left of S4
10cm, right of S4
The correct Answer is:a.
We have to consider four refractions at S1,S2,S3andS4 respectively. At each refraction, we will apply single surface refraction equation.
For refractive at first surface S1:
3/2υ1−1(−18)=0
υ1=−27cm
First image lies to the left of S1 .
For refractive at second surface S2:
1υ2−3/2−(27+9)=(1−3/2)+9
υ2=−727cm
Note that origin of Cartesian coordinate system lies at vertex of surface S2. The object distacne is (27+9)cm . The second image lies to left of S2.
For refractive at third surface S3:
u3=−(727+18)=−1987
1.5υ3−1(−198/7)=(1.5−1)(−9)
υ3=−16.5cm
For refractive at fourth surface S4:
u4=−(16.5+9)=−25.5cm
1υ4−3/2(−25.5)=(1−3/2)∞=0
υ4=−17cm
The final image lies at 17cm to the left of surface S4.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Assertion-Reasoninig
2 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Linked Comprehension
51 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Subjective
26 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
27 Videos
Similar Questions
A sphere of radius 2R and mas M has a spherical cavity of radius R as shown in the figure. Find the value of gravitational field at a point P at a distance of 6R from centre of the sphere.

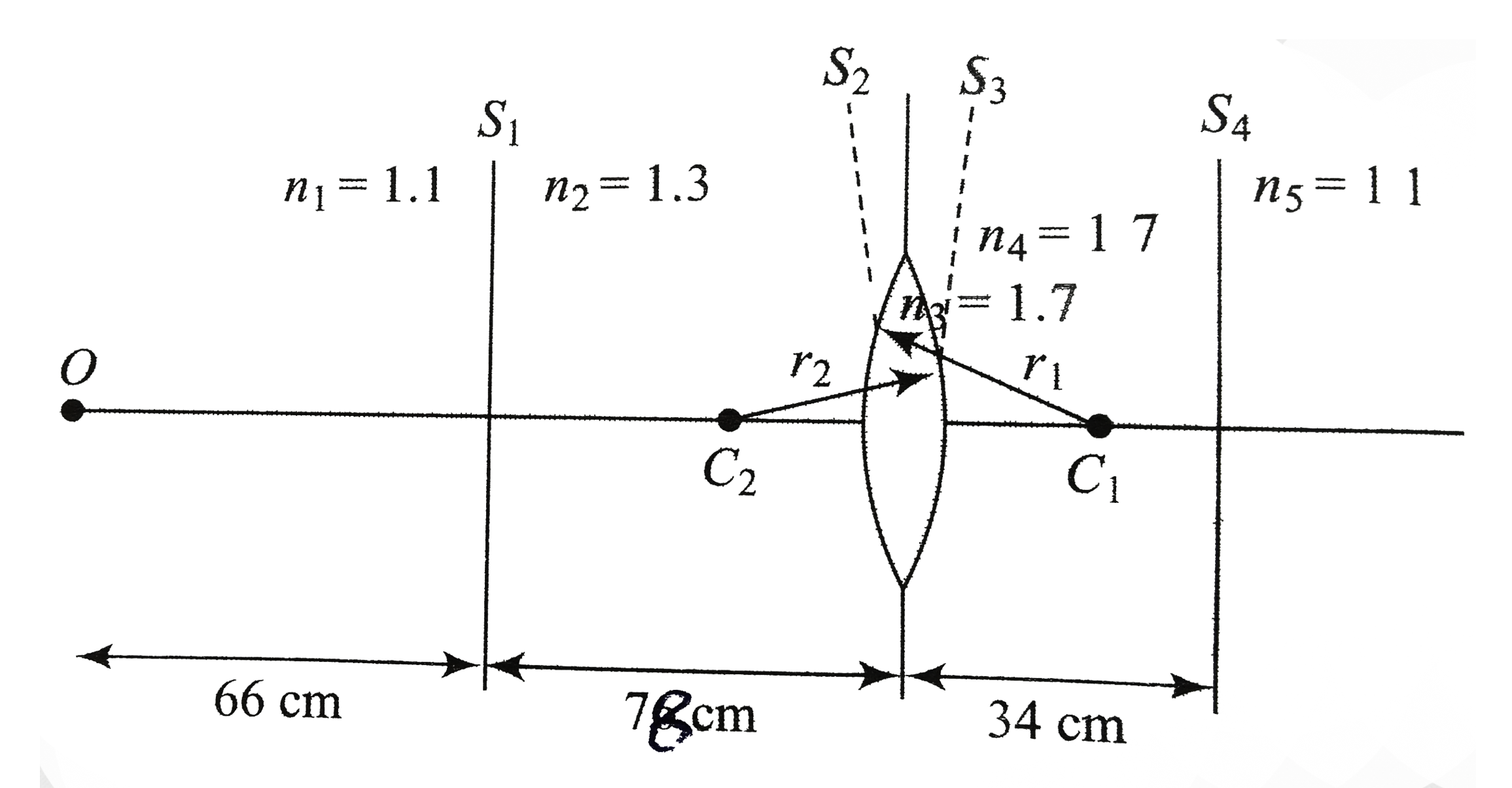
View SolutionA biconvex lens separates two media of refractive indices 1.3 and 1.7. the refractive index of the lens is 1.5 and the radii of curvature of the two sides of the lens are r1=10cm and r2=60cm .
The medium of refractive index 1.3 extends to 78 cm from the lens and that of refractive index 1.7 extends of 34 cm from the lens. A luminous object O is at a distance of 144 cm from the lens. Find the position of the final image from the lens.
View Solution
Knowledge Check
A double convex lens made of glass of refractive index 1.56 has both radii of curvature of magnitude 20cm. If an object is placed at a distance of 10cm from this lens, find the position of image formed.
A22.86 same side of the objectB22.86 opposite side of the objectC44.89 same side of the objectD44.89 opposite side of the object.
There is a spherical glass shell of refractive index 1.5, inner radius 10 cm and outer radius 20 cm. Inside th espherical cavity, there is air. A point object is placed at a point O at a distance of 30cm from the outer spherical surface. Find the final position of th eimage as seen eye.

View SolutionIn a spherical paper weight (R = 10 cm) made of glass of refractive index μ=32, an object is embedded at a distance 5 cm from its centre. What is the apparent position of the object when seen from the opposite side (see figure)?
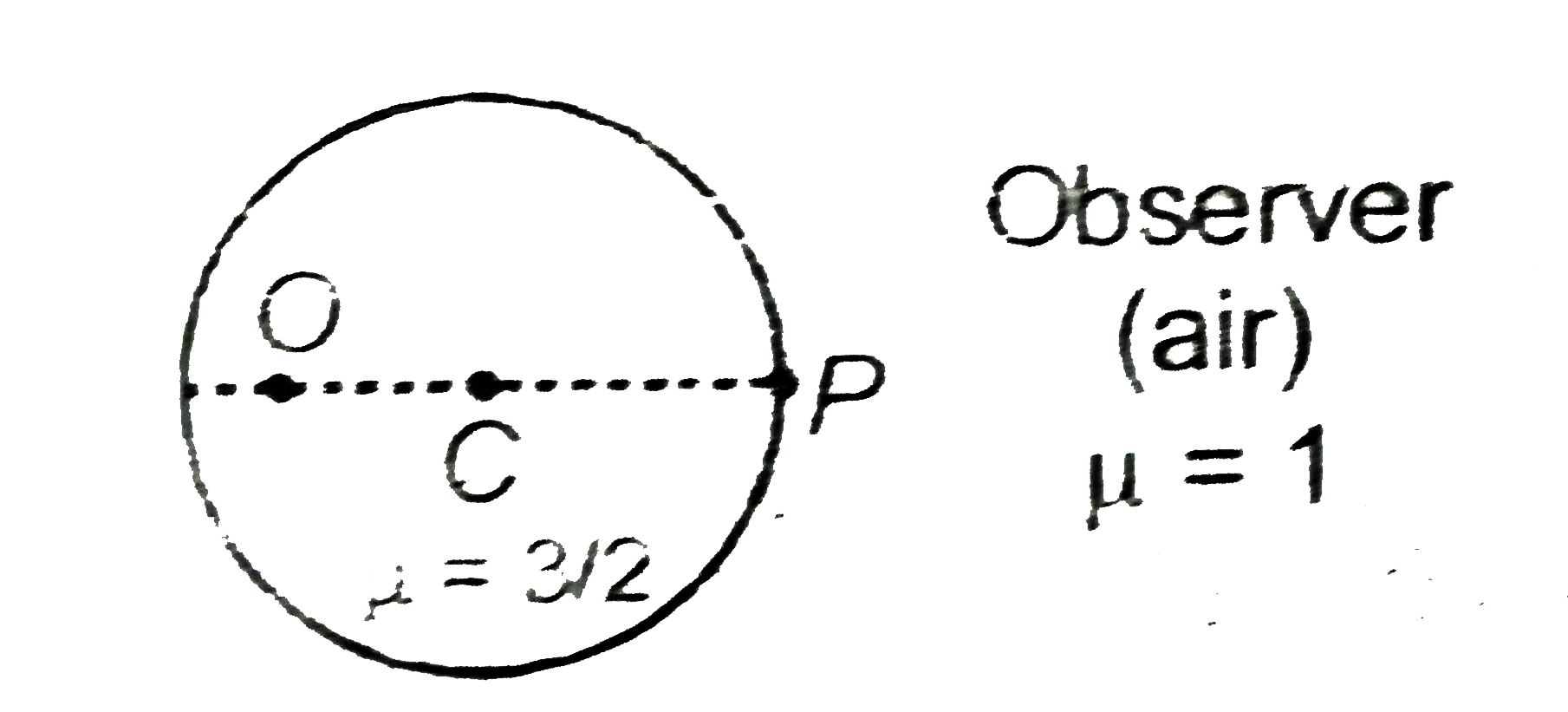
View SolutionA glass sphere of radius 2R and refractive index n has a spherical cavity of radius R, concentric with it.
Q. When viewer is on right side of the hollow sphere, what will be apparent change in position of the object?

View SolutionIn a medium of refractive index 1.6 and having a convex surface has a point object in it at a distance of 12 cm from the pole. The radius of curvature is 6 cm. Locate the image as seen from air
View SolutionA glass sphere of radius 2R and refractive index n has a spherical cavity of radius R, concentric with it.

Q. When viewer is ono left side of the hollow sphere, what will be the shift in position of the object?
View SolutionA glass sphere, refractive index 1.5 and radius 10cm, has a spherical cavity of radius 5cm concentric with it. A narrow beam of parallel light is directed into the sphere. Find the final image and its nature.

View SolutionA denser medium of refractive index 1.5 has a concave surface of radius of curvature 12 cm. An object is situated in the denser medium at a distance of 9 cm from the pole. Locate the image due to refraction in air.
View Solution
