A current carrying loop free to turn is placed in a uniform magnetic field. What will be its orientation relative to the rection of magnetic field in the equilibrium state?
To solve the problem, we need to determine the orientation of a current-carrying loop in a uniform magnetic field when it reaches an equilibrium state. Here’s a step-by-step solution:
Step 1: Understand the Concept of Torque
In a magnetic field, a current-carrying loop experiences a torque. The torque (τ) acting on the loop is given by the equation:
τ=m×B
where m is the magnetic moment of the loop and B is the magnetic field vector.
Hint: Remember that torque is a vector quantity and depends on the angle between the magnetic moment and the magnetic field.
Step 2: Condition for Equilibrium
For the loop to be in equilibrium, the net torque acting on it must be zero:
τ=0
This implies that the cross product of the magnetic moment and the magnetic field must be zero:
m×B=0
Hint: Think about what it means for the cross product to be zero. It indicates that the two vectors are either parallel or anti-parallel.
Step 3: Analyze the Magnetic Moment
The magnetic moment (m) of the loop is defined as:
m=I⋅A
where I is the current flowing through the loop and A is the area vector of the loop, which is perpendicular to the plane of the loop.
Hint: The direction of the area vector is determined by the right-hand rule based on the direction of the current.
Step 4: Determine the Orientation
For the torque to be zero, the area vector (A) must be aligned with the magnetic field vector (B). This means that the angle θ between the area vector and the magnetic field must be either 0° or 180°:
sin(θ)=0
This implies that θ=0° or θ=180°.
Hint: Consider what these angles mean in terms of the loop's orientation with respect to the magnetic field.
Step 5: Conclusion
In equilibrium, the current-carrying loop will orient itself such that its area vector is parallel to the direction of the magnetic field. If the magnetic field is directed upwards, the loop will lie flat in the plane perpendicular to the magnetic field.
Thus, the final orientation of the current-carrying loop in the equilibrium state is such that the plane of the loop is perpendicular to the direction of the magnetic field.
Final Answer: The orientation of the current-carrying loop in equilibrium is such that its area vector is parallel to the magnetic field vector.
In a magnetic field, a current-carrying loop experiences a torque. The torque (τ) acting on the loop is given by the equation:
τ=m×B
where m is the magnetic moment of the loop and B is the magnetic field vector.
For the loop to be in equilibrium, the net torque acting on it must be zero:
τ=0
This implies that the cross product of the magnetic moment and the magnetic field must be zero:
m×B=0
The magnetic moment (m) of the loop is defined as:
m=I⋅A
where I is the current flowing through the loop and A is the area vector of the loop, which is perpendicular to the plane of the loop.
For the torque to be zero, the area vector (A) must be aligned with the magnetic field vector (B). This means that the angle θ between the area vector and the magnetic field must be either 0° or 180°:
sin(θ)=0
This implies that θ=0° or θ=180°.
In equilibrium, the current-carrying loop will orient itself such that its area vector is parallel to the direction of the magnetic field. If the magnetic field is directed upwards, the loop will lie flat in the plane perpendicular to the magnetic field.
Topper's Solved these Questions
- ELECTROMAGNETICSBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - PROBLEMS (LEVEL -I)
40 Videos
- ELECTROMAGNETICSBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - PROBLEMS (LEVEL -II)
40 Videos
- ELECTROMAGNETICSBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - EXERCISE (SHORT ANSWER QUESTIONS)
6 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - EXERCISE -II
22 Videos
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
5 Videos
Similar Questions
Knowledge Check
A current carrying loop is placed in a uniform magnetic field. The torque acting on it does not depend upon
Aarea of loopBvalue of currentCmagnetic fieldDNone of these
A current carrying loop is free to turn in a uniform magnetic field. The loop will then come into equilibrium vhen its plane is inclined at
View SolutionA current carrying loop in a uniform magnetic field will experience
View SolutionWhen a current carrying coil is placed in a uniform magnetic field with its magnetic moment anti-parallel to the field.
View SolutionWhen a current carrying coil is placed in a uniform magnetic field with its magnetic moment anti-parallel to the field.
View SolutionA current loop placed in a magnetic field behaves like a
View Solutionthe force on current carrying wire placed in uniform magnetic field B as shown in figure is
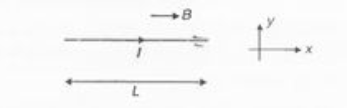
View SolutionA current carrying loop is placed in the non-uniform magnetic field whose variation in space is shown in fig. Direction of magnetic field is into the plane of paper. The magnetic force experienced by the loop is
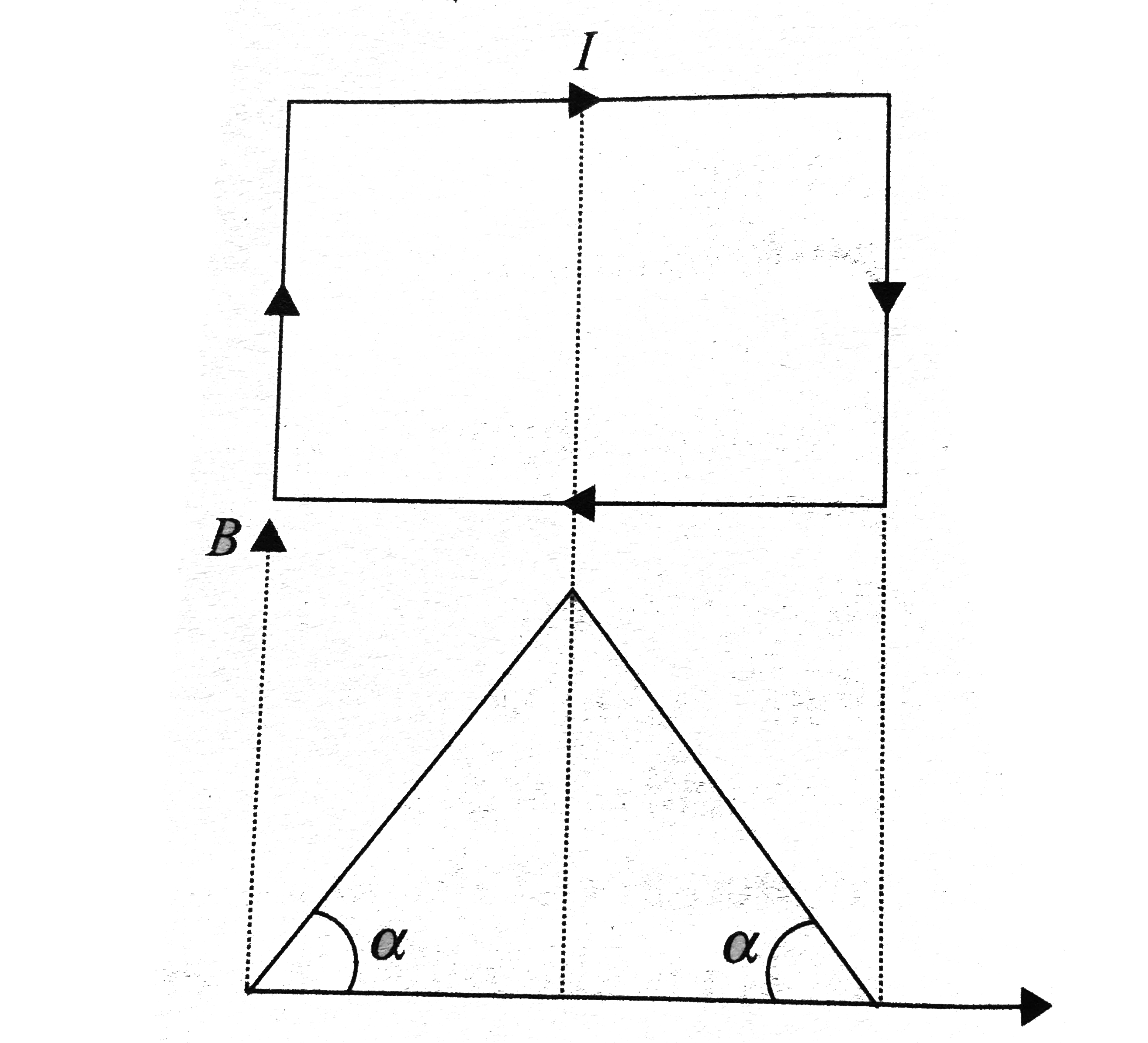
View Solution

