What is the work done in taking a north pole of strength m around a long and straight conductor in a circular path at a perpendicular distance of r from the straight conductor?
To solve the problem of calculating the work done in taking a north pole of strength m around a long and straight conductor in a circular path at a perpendicular distance r from the conductor, we can follow these steps:
1. Understand the Concept of Work Done:
Work done W is defined as the product of the force F acting on an object and the displacement d of that object in the direction of the force. Mathematically, it can be expressed as:
W=F⋅d=F⋅d⋅cos(θ)
where θ is the angle between the force and displacement vectors.
2. Identify the Force Acting on the Magnetic Pole:
The force F acting on the north pole of strength m in a magnetic field B is given by:
F=m⋅B
We need to determine the magnetic field B at a distance r from the long straight conductor carrying current i.
3. Calculate the Magnetic Field B:
The magnetic field B around a long straight conductor carrying current i at a distance r is given by:
B=μ0i2πr
where μ0 is the permeability of free space.
4. Substitute B into the Force Equation:
Now, substituting the expression for B into the force equation, we get:
F=m⋅(μ0i2πr)=μ0im2πr
5. Determine the Displacement:
When the north pole moves in a circular path around the conductor at a distance r, the displacement d is equal to the circumference of the circle:
d=2πr
6. Calculate the Work Done:
Since the angle θ between the force and displacement is 0∘ (both are in the same direction), we can simplify the work done to:
W=F⋅d=(μ0im2πr)⋅(2πr)
The 2πr terms cancel out:
W=μ0im
Final Answer:
The work done in taking a north pole of strength m around a long and straight conductor in a circular path at a perpendicular distance r from the conductor is:
W=μ0im
Work done W is defined as the product of the force F acting on an object and the displacement d of that object in the direction of the force. Mathematically, it can be expressed as:
W=F⋅d=F⋅d⋅cos(θ)
where θ is the angle between the force and displacement vectors.
The force F acting on the north pole of strength m in a magnetic field B is given by:
F=m⋅B
We need to determine the magnetic field B at a distance r from the long straight conductor carrying current i.
The magnetic field B around a long straight conductor carrying current i at a distance r is given by:
B=μ0i2πr
where μ0 is the permeability of free space.
Now, substituting the expression for B into the force equation, we get:
F=m⋅(μ0i2πr)=μ0im2πr
When the north pole moves in a circular path around the conductor at a distance r, the displacement d is equal to the circumference of the circle:
d=2πr
Since the angle θ between the force and displacement is 0∘ (both are in the same direction), we can simplify the work done to:
W=F⋅d=(μ0im2πr)⋅(2πr)
The 2πr terms cancel out:
W=μ0im
The work done in taking a north pole of strength m around a long and straight conductor in a circular path at a perpendicular distance r from the conductor is:
W=μ0im
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - PROBLEMS (LEVEL -I)40videos
ELECTROMAGNETICS
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - PROBLEMS (LEVEL -II)40videos
ELECTROMAGNETICS
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - EXERCISE (SHORT ANSWER QUESTIONS)6videos
ELECTROMAGNETICS
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - EXERCISE -II22videos
ELECTROMAGNETIC WAVES
- BOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)5videos
ELECTROSTATICS
Similar Questions
How much work is done in taking an electron around a nucleus in a circular path?
View SolutionA magnetic pole of strength 4 Am is moved twice around a long straight wire carrying a current of 3A. The work done is
View SolutionA straight conductor of length 32 cm carries a current of 30A. Magnetic induction at a point which is in air at a perpendicular distance of 12cm from the mid point of the conductor is
View SolutionFind the magnetic induction due to a straight conductor of length 16cm carrying current of 5A at a distance of 6cm from the midpoint of conductor
View SolutionA square loop, carrying a steady current I, is placed in a horizontal plane near a long straight conductor carrying a steady current I1 at a distance d from the donductor as shown in figure. The loop will experience
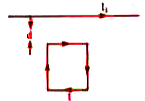 View Solution
View SolutionA current 'I' flows along an infinitely long straight conductor. If 'r' is the perpendicular distance of a point from the lower end of the conductor, then the magnetic induction B is given by
View SolutionAn electron is ejected from the surface of a long, thick straight conductor carrying a current, initially in a direction perpendicular to the conductor. The electron will
View SolutionA long straight vertical conductor carries a current of 8A in the upward direction. What the magnitude of the resultant magnetic induction at a point in the horizonatal plane at a distance of 4 cm from the conductor towards South? (The horizontal compo-nent of earth's magnetic induction =4×10−5T)
View SolutionWhat is the amount of work done in moving a point charge around a circular are of radius r at the centre where another point charge is located ?
View Solution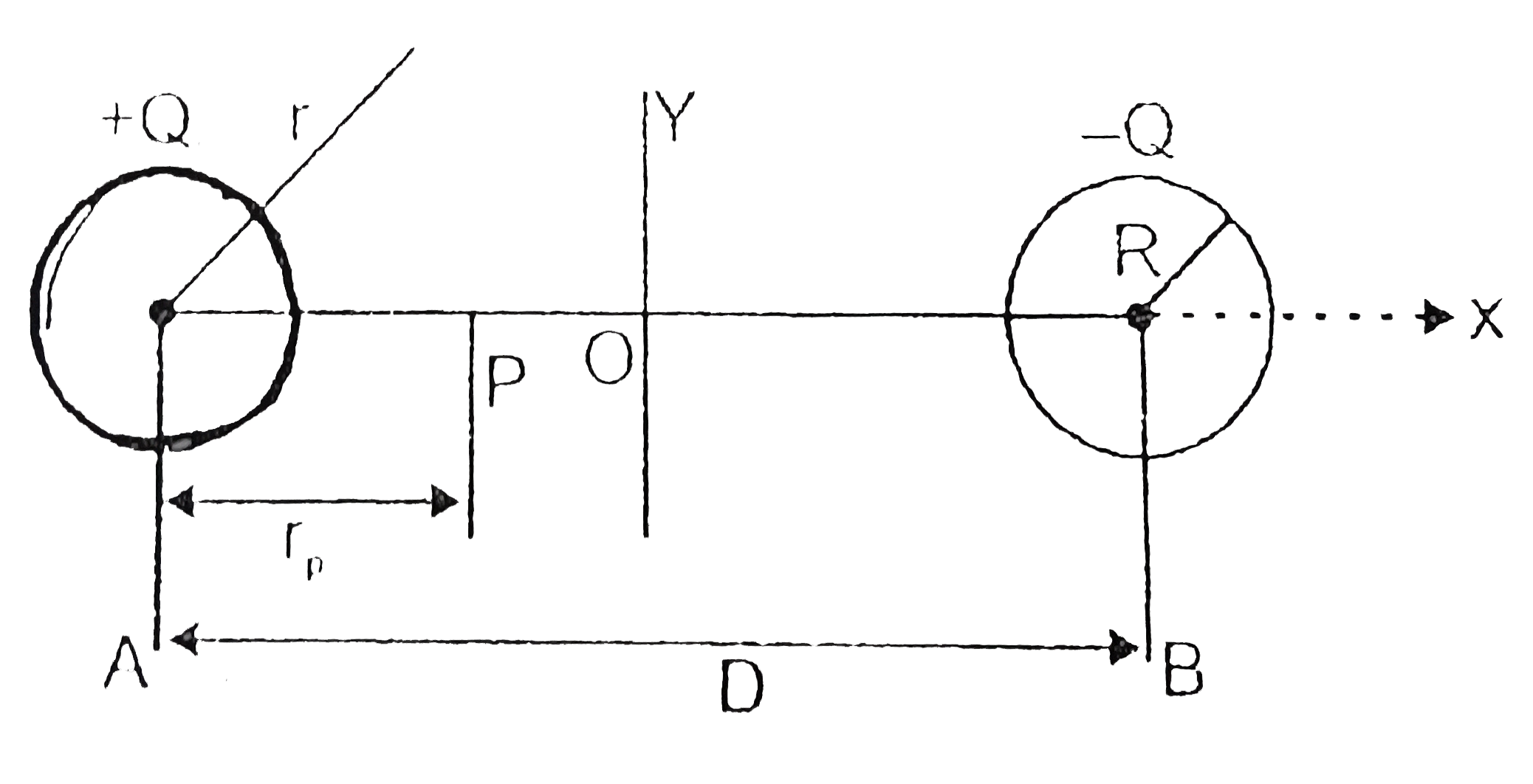
The figure shows two identical long straight metal wires, A and B placed parallel to z-axis the cross sectional radius of each wire is R and the separation of the two wires is D>>R. The electric potential at a perpendicular distance r>R from a long straight wire due to that wire is given by V=−kln(rR) where k is a positive constant. the wires carry charges +Q and −Q per unit length respectively. Then
Q. As D>>R, the electric field due to a long straight wire has cylindrical symmetry. The charge per unit length of the wire isView Solution
