A current I flows in a circuit shaped like an isosceles trapizium. The ratio of the bases is 2. The length of the smaller base is l. Calculate the megnetic field induction at point P located in the plane of the trapizium, but at a distance a from the midpoint of the smaller base,

From similar triangles APF and CPE, we find d=2a and
tanα=12a. Magnetic field at P due to wire 1 is
B1=μ0I4πd[sinα−sin(−α)]=μ0Isinα2πd=μ0Isinα4πa
The direction of the magnetic field is into the plane of the paper.
α is the half-angle subtended by the wire 1 at point P and d is the
perpendicular distance between the wire and point P.

Magnetic field at P due to wires (2) and (4) is zero.
Megnetic field at P due to wire 3 is
B=B3−B1=μ0Isinα2πa−μ0Isinα4πa=μ0Isinα4πa
or B=μ0I4πa[1√l2+4a2]
out of the plane of the paper.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Solved Example20videos
SOURCES OF MAGNETIC FIELD
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Concept Exercise 2.135videos
SOURCES OF MAGNETIC FIELD
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.612videos
RAY OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Comprehension Type14videos
WAVE OPTICS
Similar Questions
A current I=√2 A flows in a circuit having the shape of isosceles trapezium. The ratio of the bases of the trapezium is 2. Find the magnetic induction B at symmetric point O in the plane of the trapezium. The length of the smaller base of the trapezium is 100mm and the distance r=50mm.
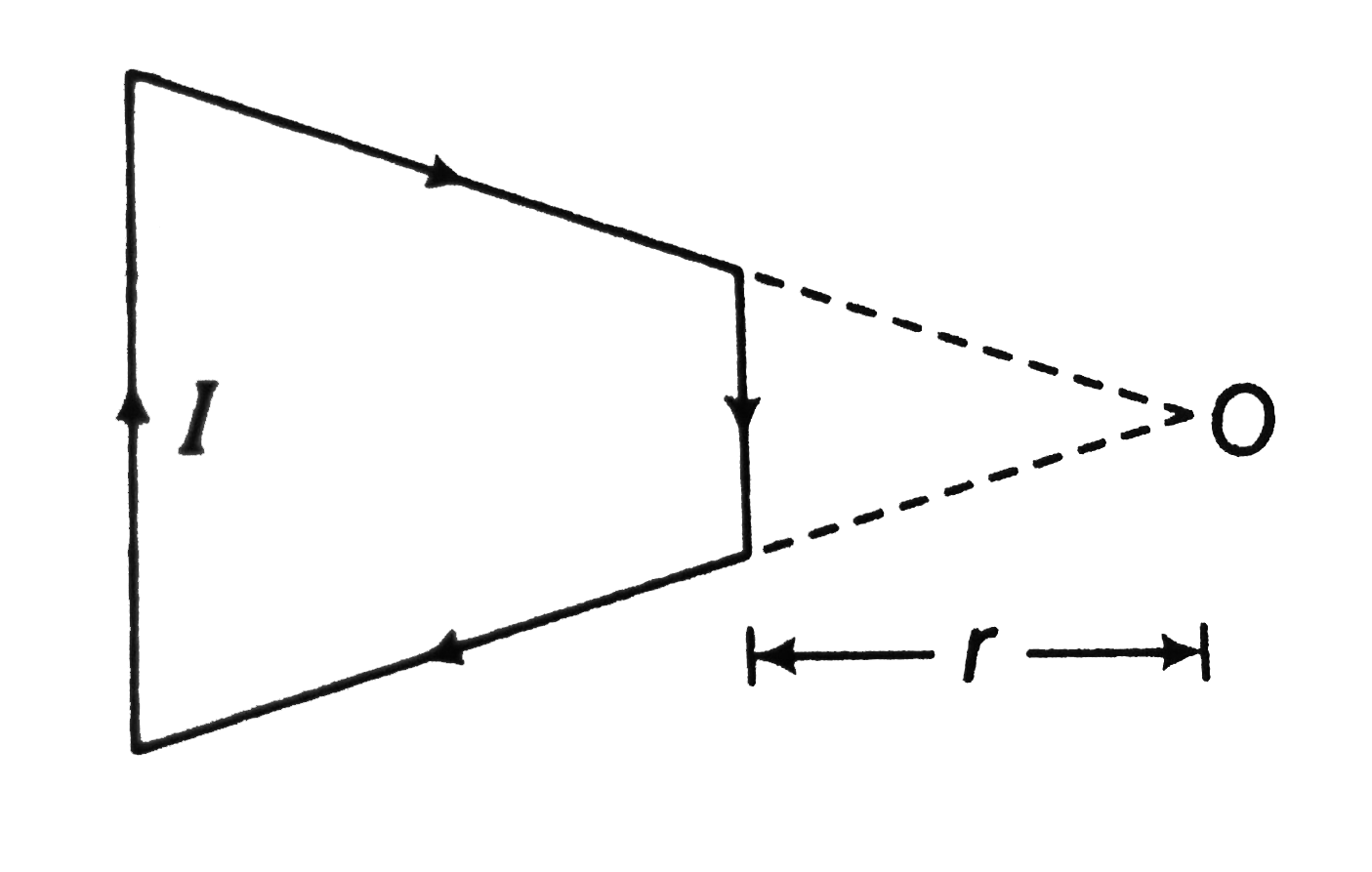 View Solution
View SolutionA rod of length l, has a uniform positive charge per unit length and a total charge Q. calculate the electric field at a point P located along the long axis of the rod and at a distance a from one end
 View Solution
View SolutionTwo long parallel wires carry equal current I flowing in the same direction are at a distance 2d apart. The magnetic field B at a point lying on the perpendicular line joining the wires and at a distance x from the midpoint is
View SolutionDerive an expression for the magnetic field at a point on the axis located at a distance x from the centre of a magnetic dipole of length 2l and magnetic moment M.
View SolutionFigure shows a cross-section of a long ribbon of width ω that is carrying a uniformly distributed total current i into the page. Calculate the magnitude and direction of the magnetic field B at a point P in the plane of the ribbon at a distance d from its edge.
 View Solution
View SolutionFigure shows a straight wire of length a carrying a current I. What is the magnitude of magnetic field induction produced by the current at P, which is lying at a perpendicular distance a from one end of the wire.

 View Solution
View SolutionTwo long straight parallel wieres are 2m apart, perpendicular to the plane of the paper. The wire A carries a current of 9.6A, directed into the plane of the paper. The wire B carries a current such that the magnetic field of induction at the point P, at a distance of 1011 m from the wire B, is zero. find
a. the magnitude and directiion of the current in B.
b. the magnitude of the magnetic field of induction of the pont S.
c. the force per unit length on the wire B.
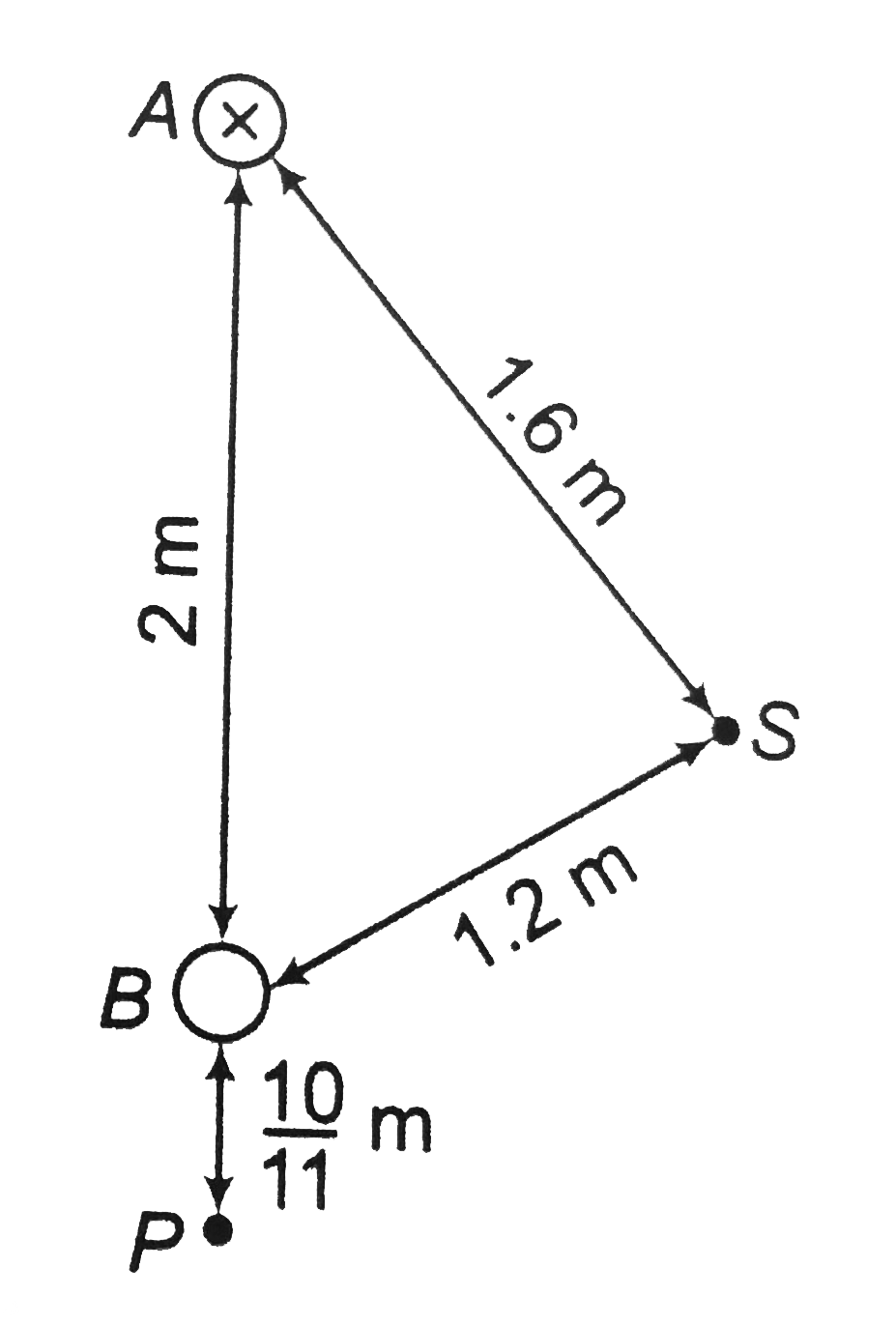 View Solution
View SolutionA circular coil of radius 2R is carrying current 'i' . The ratio of magnetic fields at the centre of the coil and at a point at a distance 6R from the centre of the coil on the axis of the coil is
View SolutionIn Fig. two long parallel wires (seen end-on) that are a distance R apart carry equal currents i in the same sense. Find the magnitude of the magnetic field at point P , which lies quidistant from the two wires at an angle θ from the plane of the wires.
 View Solution
View SolutionAn arbitrary shaped closed coil is made of a wire of length L and a current I ampere is flowing in it. If the plane of the coil is perpendicular to megnetic field →B, the force on the coil is
View Solution

