A cylinder is rotating with angular velocity ω0 and is gently put on a rough horizontal floor. Assume mass of the cylinder is m and radius R. Calculate the velocity of cylinder when it starts pure rolling on the surface.
To solve the problem of a cylinder rotating with an initial angular velocity ω0 and transitioning to pure rolling on a rough horizontal surface, we can follow these steps:
Step 1: Understand the Initial Conditions
The cylinder is initially rotating with an angular velocity ω0 and has a radius R. When it is placed on the rough surface, the bottommost point of the cylinder tends to move backward due to its rotation.
Step 2: Identify the Forces Acting on the Cylinder
When the cylinder touches the rough surface, a frictional force f acts on it in the forward direction. This frictional force is responsible for the acceleration of the center of mass of the cylinder.
Step 3: Write the Equations of Motion
- The linear acceleration a of the cylinder can be expressed as:
a=fm
where m is the mass of the cylinder.
- The angular acceleration α can be expressed using the torque produced by the frictional force:
α=τI
where τ=fR (torque due to friction) and I=12mR2 (moment of inertia of a solid cylinder). Thus,
α=fR12mR2=2fmR
Step 4: Relate Linear and Angular Quantities
Using the kinematic equations, we can express the linear and angular velocities:
- Linear velocity v after time t:
v=u+at=0+fmt=ftm
- Angular velocity ω after time t:
ω=ω0+αt=ω0−2fmRt
Step 5: Condition for Pure Rolling
For pure rolling to occur, the condition v=ωR must be satisfied. Substituting the expressions for v and ω:
ftm=(ω0−2fmRt)R
Step 6: Solve for Linear Velocity
Rearranging the equation:
ftm=ω0R−2ftm
Combining terms gives:
ftm+2ftm=ω0R
3ftm=ω0R
Thus, we can express f in terms of v:
f=mω0R3t
Step 7: Substitute Back to Find v
Now substituting f back into the equation for v:
v=ftm=mω0R3t⋅tm=ω0R3
Conclusion
The linear velocity v of the cylinder when it starts pure rolling on the surface is:
v=ω0R3
The cylinder is initially rotating with an angular velocity ω0 and has a radius R. When it is placed on the rough surface, the bottommost point of the cylinder tends to move backward due to its rotation.
When the cylinder touches the rough surface, a frictional force f acts on it in the forward direction. This frictional force is responsible for the acceleration of the center of mass of the cylinder.
- The linear acceleration a of the cylinder can be expressed as:
a=fm
where m is the mass of the cylinder.
α=τI
where τ=fR (torque due to friction) and I=12mR2 (moment of inertia of a solid cylinder). Thus,
α=fR12mR2=2fmR
Using the kinematic equations, we can express the linear and angular velocities:
- Linear velocity v after time t:
v=u+at=0+fmt=ftm
- Angular velocity ω after time t:
ω=ω0+αt=ω0−2fmRt
For pure rolling to occur, the condition v=ωR must be satisfied. Substituting the expressions for v and ω:
ftm=(ω0−2fmRt)R
Rearranging the equation:
ftm=ω0R−2ftm
Combining terms gives:
ftm+2ftm=ω0R
3ftm=ω0R
Thus, we can express f in terms of v:
f=mω0R3t
Now substituting f back into the equation for v:
v=ftm=mω0R3t⋅tm=ω0R3
The linear velocity v of the cylinder when it starts pure rolling on the surface is:
v=ω0R3
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - NCERT FILE ( NCERT TEXTBOOK EXERCISES )
21 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - NCERT FILE ( NCERT (ADDITIONAL EXERCISES) )
12 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Conceptual Questions
24 Videos
- PHYSICAL WORLD BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)
6 Videos
- THERMAL PROPERTIES OF MATTERBOOK - MODERN PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
A cylinder rotating with angular velocity ω0 is put on a rough horizontal floor so that edge touches a vertical rough wall. Rotational motion of the cylinder is retarded and after some time cylinder comes to rest. If m is mass of cylinder and R is its radius then calculate number of revolutions made by the cylinder before it comes to rest. Assume μ is coefficient of friction for floor as well as wall.
View SolutionA solid cylinder of mass 20kg rotates about its axis with angular velocity of 100 radian s−1. The radius of the cylinder is 0.25m. The magnitude of the angular momentum of the cylinder about its axis of rotation is
View Solution
Knowledge Check
A hoop of radius r mass m rotating with an angular velocity ω0 is placed on a rough horizontal surface. The initial velocity of the centre of the hoop is zero. What will be the velocity of the centre of the hoop when it cases to slip ?
Arω02Brω0Crω04Drω03A hoop of radius r and mass m rotating with an angular velocity ω0 is placed on a rough horizontal surface. The initial velocity of the centre of the hoop is zero. What will be the velocity of the centre of the hoop when it ceases ot slip?
Arω04Brω03Crω02Drω0Three identical cylinders of radius R are in contact.Each cylinder is rotating with angular velocity ω.A thin belt is moving without sliding on the cylinders. Calculate the magnitude of velocity of point P with respect to Q.P and Q are two points of belt which are in contact with the cylinder.
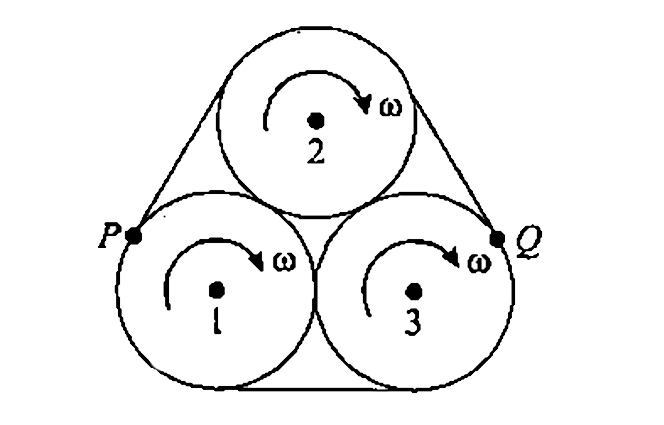 A2RωBRωCRω/2DRω/√3
A2RωBRωCRω/2DRω/√3
An cylinder of mass m is rotated about its axis by an angular velocity ω and lowered gently on an inclined plane as shown in figure. Then :
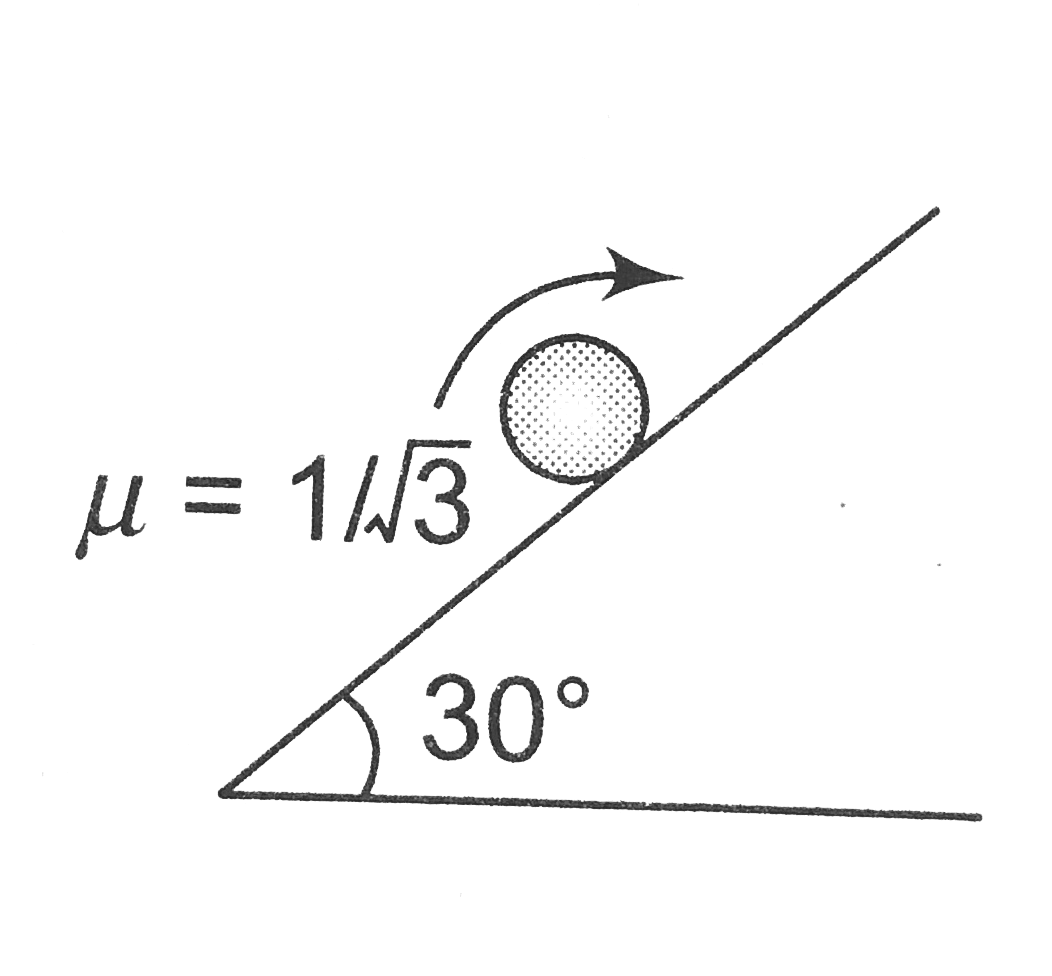 .
.
View SolutionA uniform ring of radius R is given a back spin of angular velocity V0/2R and thrown on a horizontal rough surface with velocity of centre to be V0. The velocity of the centre of the ring when it starts pure rolling will be
View SolutionA point mass m collides with a disc of mass m and radius R resting on a rough horizontal surface as shown . Its collision is perfectly elastic. Find angular velocity of the disc after pure rolling starts

View SolutionA solid sphere with a velocity (of centre of mass) v and angular velocity ω is gently placed on a rough horizontal surface. The frictional force on the sphere :
View Solution
A uniform solid cylinder of mass m and radius R is placed on a rough horizontal surface. A horizontal constant force F is applied at the top point P of the cylinder so that it start pure rolling. The acceleration of the cylinder is
View Solution
