A cylinder of mass m rests on a supporting block as shown. If β=60∘ and θ=30∘, calculate the maximum acceleration 'a' which the block may be given up the incline so that the cylinder does not lose contact at B. Neglect friction anywhere).

g/2
g
g/3
g/4
The correct Answer is:B
Step by step video, text & image solution for A cylinder of mass m rests on a supporting block as shown. If beta=60^(@) " and " theta=30^(@), calculate the maximum acceleration 'a' which the block may be given up the incline so that the cylinder does not lose contact at B. Neglect friction anywhere). by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
A block of metal is lying on the floor of a bus. The maximum acceleration which can be given to the bus so that the block may remain at rest, will be -
View SolutionA cylinder of mass m and radius R rolls down an inclined plane of inclination θ. Calculate the linear acceleration of the axis of cylinder.
View Solution
Knowledge Check
A block of mass m is placed on the top of another block of mass M as shown in the figure. The coefficient of friction between them is μ.

The maximum acceleration with which the block M may move so that m also moves along with it isAμgBμMmgCμmMgDgμA block is kept on a smooth inclined plane of angle of inclination θ that moves wuth a contact acceleration so that the block does not slide relative to the inclined plane. If the inclined plane stops the normal contact force offered by the plane on the block changes by a factor
AtanθBtan2θCcos2θDcotθ
A cylinder of mass m and radius R rolls down an inclined plane of inclination θ. Calculate the linear acceleration of the axis of cylinder.
View SolutionIn the fig. shown, the pulley and string are mass less and the incline is frictionless. The segment AP of the string is parallel to the incline and the segment PB is perpendicular to the incline. End of the string is pulled with a constant force F.
(a) If the block is moving up the incline with acceleration while being in contact with the incline , then angle θ must be less than θ0. Find θ0
If θ=θ02 find the maximum acceleration with which the block can move up the plane without losing contact with the incline.

View SolutionA block of mass m is placed on the rough incline of a wedge of mass M and inclination α to the horizontal. Calculate the maximum and minimum acceleration that can be imparted to the wedge so that the block may remain stationary relative to the wedge. The coefficient iof friction between the block and the wedge is μ.
View SolutionA block of mass 1.0 kg rests on a wedge of angle θ. The acceleration which should be given to the wedge so that the block falls freely is :
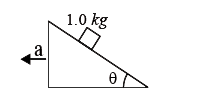
View SolutionA system consists of block A and B each of mass m connected by a light spring as shown in the figure with block B in contact with a wall. The block A compresses the spring by 3mg/k from natural length of spring and then released from rest. Neglect friction anywhere.
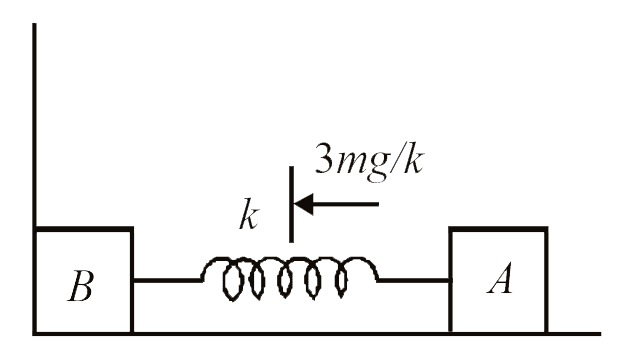
Maximum extension in the spring after system loses contact with wall
View SolutionA system consists of block A and B each of mass m connected by a light spring as shown in the figure with block B in contact with a wall. The block A compresses the spring by 3mg/k from natural length of spring and then released from rest. Neglect friction anywhere.
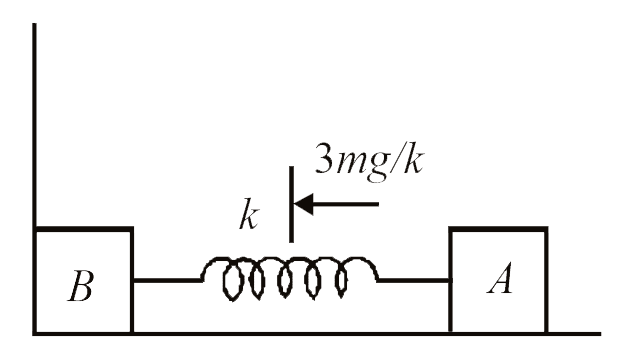
Velocity of centre of mass of system comprising A and B when block B just loses contact with the wall
View Solution
