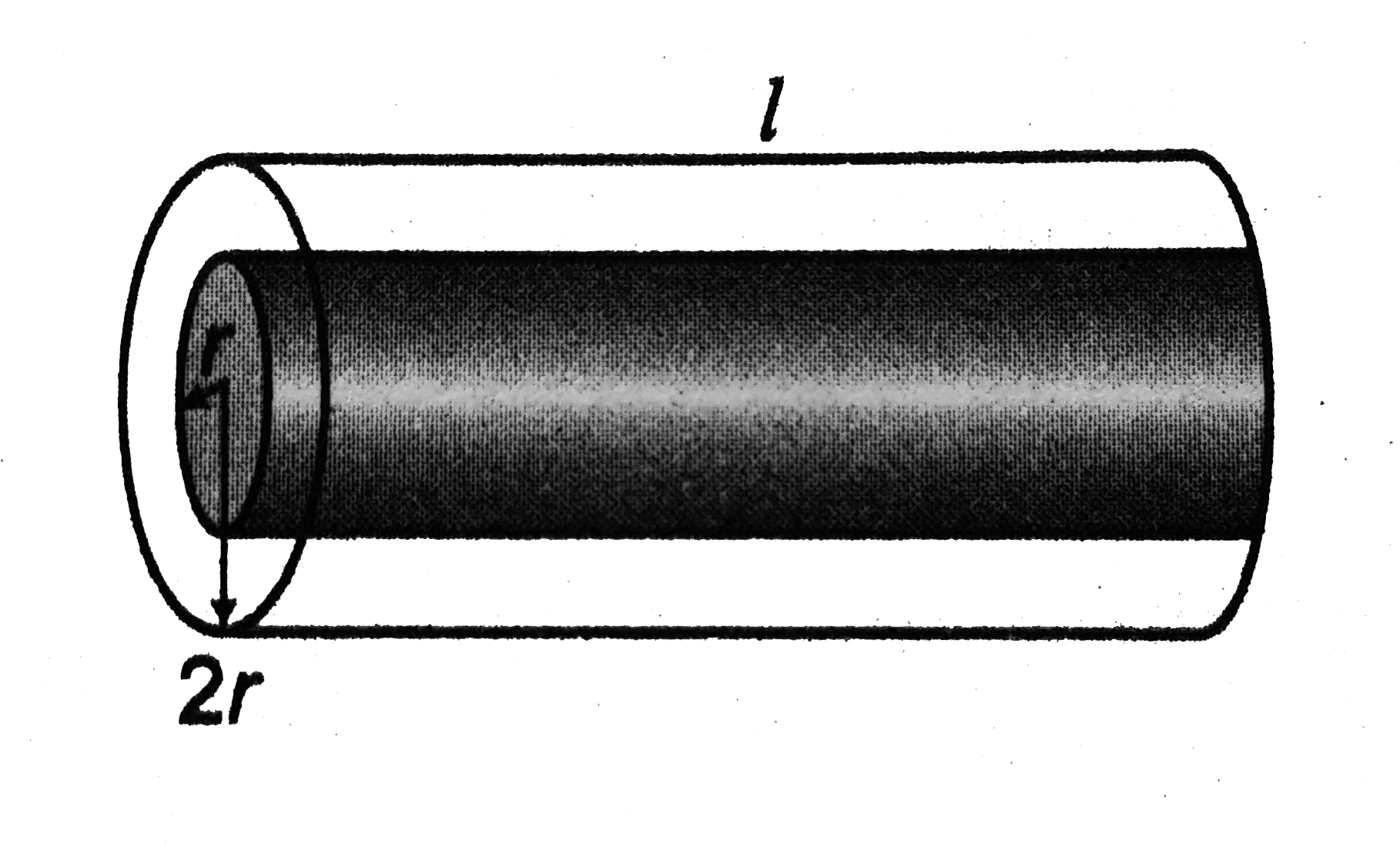
A cylinder of radius R made of a material of thermal conductivity K1 is surrounded by a cylindrical shell of inner radius R and outer radius 2R made of a material of thermal conductivity K2. The two ends of the combined system are maintained at two different temperatures. There is no loss of heat across the cylindrical surface and the system is in steady state. The effective thermal conductivity of the system is
(a) K1+K2 (b) K1K2/(K1+K2)
(c )(K1+3K2)/4
(d) (3K1+K2)/4.
The correct Answer is:A
To find the effective thermal conductivity of the given system, we will analyze the heat transfer through the inner cylinder and the outer cylindrical shell step by step.
Step 1: Identify the Components
We have:
- An inner cylinder of radius R and thermal conductivity K1.
- An outer cylindrical shell with inner radius R and outer radius 2R, made of a material with thermal conductivity K2.
Step 2: Write the Heat Flow Equations
In steady state, the heat flow through both the inner cylinder and the outer shell must be equal.
The heat flow ΔQ through a cylindrical surface can be expressed as:
ΔQ=K⋅A⋅ΔTL
where:
- K is the thermal conductivity,
- A is the cross-sectional area,
- ΔT is the temperature difference,
- L is the length of the cylinder.
Step 3: Calculate the Heat Flow for the Inner Cylinder
For the inner cylinder:
- Area A1=πR2
- Heat flow through the inner cylinder:
ΔQ1=K1⋅πR2⋅ΔTL
Step 4: Calculate the Heat Flow for the Outer Cylinder
For the outer cylindrical shell:
- The area A2 is the difference between the outer and inner surfaces:
A2=π((2R)2−R2)=π(4R2−R2)=π(3R2)
- Heat flow through the outer cylinder:
ΔQ2=K2⋅π(3R2)⋅ΔTL
Step 5: Set Up the Equation for Steady State
Since the heat flow through both components is equal:
ΔQ1=ΔQ2
Substituting the expressions we derived:
K1⋅πR2⋅ΔTL=K2⋅π(3R2)⋅ΔTL
Step 6: Simplify the Equation
Cancel out common terms (π,R2,ΔT,L):
K1=3K2
Step 7: Find the Effective Thermal Conductivity
Now, we need to express the effective thermal conductivity K of the entire system. The effective thermal conductivity can be found by combining the contributions from both cylinders:
K=K1+3K24
Conclusion
Thus, the effective thermal conductivity of the system is:
K1+3K24
We have:
- An inner cylinder of radius R and thermal conductivity K1.
- An outer cylindrical shell with inner radius R and outer radius 2R, made of a material with thermal conductivity K2.
In steady state, the heat flow through both the inner cylinder and the outer shell must be equal.
ΔQ=K⋅A⋅ΔTL
where:
- K is the thermal conductivity,
- A is the cross-sectional area,
- ΔT is the temperature difference,
- L is the length of the cylinder.
For the inner cylinder:
- Area A1=πR2
- Heat flow through the inner cylinder:
ΔQ1=K1⋅πR2⋅ΔTL
For the outer cylindrical shell:
- The area A2 is the difference between the outer and inner surfaces:
A2=π((2R)2−R2)=π(4R2−R2)=π(3R2)
- Heat flow through the outer cylinder:
ΔQ2=K2⋅π(3R2)⋅ΔTL
Since the heat flow through both components is equal:
ΔQ1=ΔQ2
Substituting the expressions we derived:
K1⋅πR2⋅ΔTL=K2⋅π(3R2)⋅ΔTL
Cancel out common terms (π,R2,ΔT,L):
K1=3K2
Now, we need to express the effective thermal conductivity K of the entire system. The effective thermal conductivity can be found by combining the contributions from both cylinders:
K=K1+3K24
Thus, the effective thermal conductivity of the system is:
K1+3K24
Topper's Solved these Questions
- CALORIMETRY & HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Example Type 1
4 Videos
- CALORIMETRY & HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Example Type 2
2 Videos
- BASIC MATHEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise
13 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery
38 Videos
Similar Questions
A cylinder of radius R made of a material of thermal conductivity K1 is surrounded by cylindrical shell of inner radius R and outer radius 2R made of a material of thermal con-ductivity K2 The two ends of the combined system are maintained at two differnet tem-peratures There is no loss of heat across the cylindrical surface and system is in steady state What is the effective thermal conductivity of the system
 .
.
View SolutionA cylinder of radius r made of a material of thermal conductivity K1 is surrounded by a cylindrical shell of inner radius r and outer radius 2r made of a material of thermal conductivity K2. The two ends of the combined system are maintained at two different temperatures. There is no loss of heat across the cylindrical surface and the system is in steady state. Show that the effective thermal conductivity of the system is (K1+3K2)/4.
View Solution
Knowledge Check
A copper cylindrical tube has inner radius a and outer radius b. The resistivity is p. The resistance of . the cylinder between the two ends is
Aρlb2−a2Bρl2π(b−a)Cρlπ(b2−a2)Dπ(b2−a2)ρl
A cylinder of radius R is surrounded by a cylindrical shell of inner radius R and oputer radius 2R. The thermal conductivity of the material of the inner cylinder is k1 and that of the outer cylinder is K2 ,Assumming no loss of heat , the effective thermal conductivity of the system for heat flowing along the length of the cylinder is :
View SolutionThermal conductivity of inner core of radius r is K and of the outer one of radius 2r is 2K. Find equivalent value of thermal conductivity between its two ends.
View SolutionCalculated thermal conductance for radial flow of a spherical sheel of inner and outer radius r1and r2. Assume that thermal conductivity of the material is K
View SolutionThe ends of a rod of uniform thermal conductivity are maintained at different (constant) temperatures. Afer the steady state is achieved:
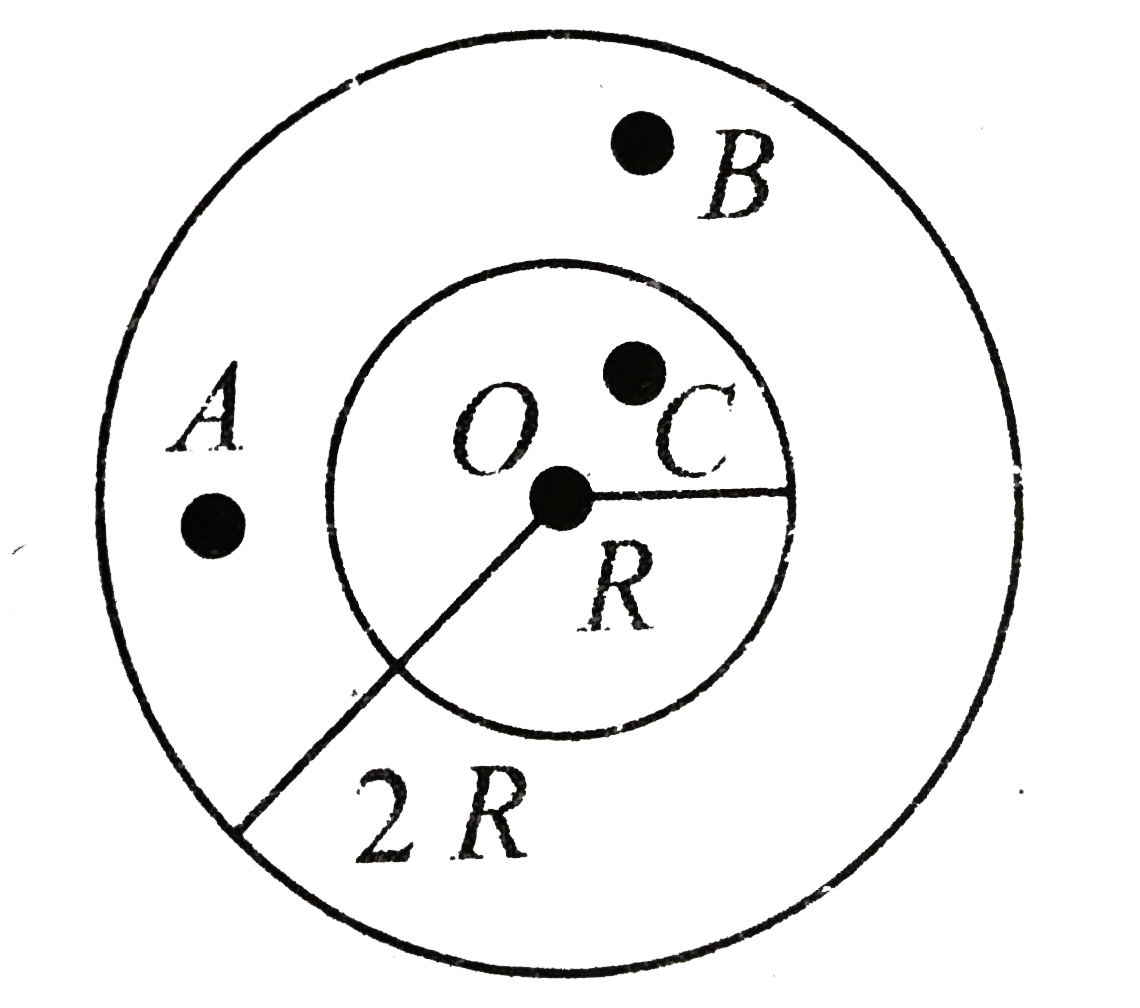
View SolutionA hollow conducting sphere of inner radius r and outer radius 2R is given charge Q as shown in figure, then the
View SolutionA cylinder of radius R and length l is made up of substance whose thermal conductivity K varies with the distance x from the axis as K=K1x+K2. Determine the the effective thermal conductivity between the flat faces of the cylinder.
View SolutionConsider a compound slab consisting of two different material having equal thickness and thermal conductivities K and 2K respectively. The equivalent thermal conductivity of the slab is
View Solution
