A cylinder wire of radius R is carrying uniformly distributed current I over its cross-section. If a circular loop of radius r is taken as amperian loop, then the variation value of ∮→B⋅→dl over this loop with radius 'r' of loop will be best represented by
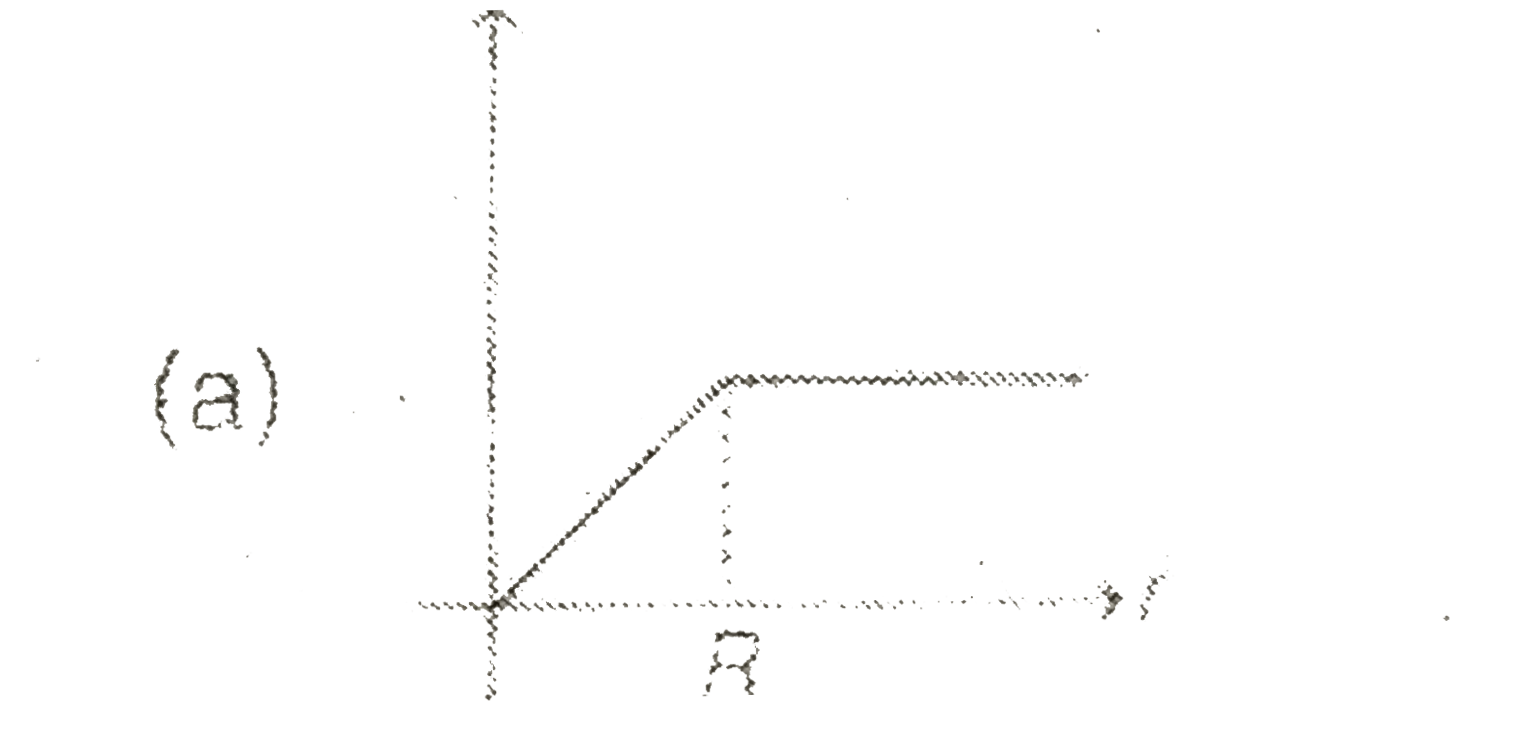


The correct Answer is:b
To solve the problem, we will analyze the magnetic field around a cylindrical wire carrying a uniformly distributed current using Ampere's Circuital Law.
1. Understanding the Setup:
We have a cylindrical wire of radius R carrying a current I uniformly distributed across its cross-section. We want to analyze the magnetic field around this wire using an Amperian loop of radius r.
2. Applying Ampere's Circuital Law:
According to Ampere's Circuital Law, the line integral of the magnetic field →B around a closed loop is equal to μ0 times the current enclosed by that loop:
∮→B⋅d→l=μ0Ienclosed
3. Determining the Current Enclosed:
- If r<R (the loop is inside the wire), we need to find the current enclosed by the loop. The current density J is given by:
J=IπR2
- The area of the circular loop of radius r is πr2. Thus, the current enclosed Ienclosed is:
Ienclosed=J×Area=(IπR2)×πr2=Ir2R2
4. Calculating the Line Integral:
- For r<R:
∮→B⋅d→l=μ0(Ir2R2)
- The left side can be simplified since →B is constant along the circular path of radius r:
B(2πr)=μ0(Ir2R2)
- Therefore, we can express B:
B=μ0Ir2πR2
5. For r≥R:
- The entire current I is enclosed, so:
∮→B⋅d→l=μ0I
- Thus, for r≥R:
B(2πr)=μ0I⟹B=μ0I2πr
6. Graphing the Results:
- For r<R, B varies linearly with r (specifically, B∝r).
- For r≥R, B decreases with r (specifically, B∝1r).
- The graph of ∮→B⋅d→l versus r will show a parabolic increase for r<R and a hyperbolic decrease for r≥R.
Conclusion:
The variation of ∮→B⋅d→l over the loop will be best represented by a curve that increases parabolically for r<R and then becomes constant for r≥R.
We have a cylindrical wire of radius R carrying a current I uniformly distributed across its cross-section. We want to analyze the magnetic field around this wire using an Amperian loop of radius r.
According to Ampere's Circuital Law, the line integral of the magnetic field →B around a closed loop is equal to μ0 times the current enclosed by that loop:
∮→B⋅d→l=μ0Ienclosed
- If r<R (the loop is inside the wire), we need to find the current enclosed by the loop. The current density J is given by:
J=IπR2
- The area of the circular loop of radius r is πr2. Thus, the current enclosed Ienclosed is:
Ienclosed=J×Area=(IπR2)×πr2=Ir2R2
- For r<R:
∮→B⋅d→l=μ0(Ir2R2)
- The left side can be simplified since →B is constant along the circular path of radius r:
B(2πr)=μ0(Ir2R2)
- Therefore, we can express B:
B=μ0Ir2πR2
- The entire current I is enclosed, so:
∮→B⋅d→l=μ0I
- Thus, for r≥R:
B(2πr)=μ0I⟹B=μ0I2πr
- For r<R, B varies linearly with r (specifically, B∝r).
- For r≥R, B decreases with r (specifically, B∝1r).
- The graph of ∮→B⋅d→l versus r will show a parabolic increase for r<R and a hyperbolic decrease for r≥R.
The variation of ∮→B⋅d→l over the loop will be best represented by a curve that increases parabolically for r<R and then becomes constant for r≥R.
Topper's Solved these Questions
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - More than One Option is Correct
25 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Comprehension type Questions
16 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Integer type Questions
10 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
- MEASUREMENT AND ERRORSBOOK - DC PANDEY ENGLISHCHAPTER - MEASUREMENT AND ERRORSEXERCISE - Subjective
19 Videos
Similar Questions
A long thick conducting cylinder of radius 'R' carries a current uniformly distributed over its cross section :
View SolutionA long, straight wire of radius R carries a current distributed uniformly over its cross section. The magnitude of the magnetic field is
View SolutionA cylindrical long wire of radius R carries a current I uniformly distributed over the cross sectional area of the wire. The magnetic field at a distance x from the surface inside the wire is
View SolutionA uniform current I is flowing in a long wire of radius R. If the current is uniformly distributed across the cross-sectional area of the wire, then
View SolutionWhat will be magnetic field at centre of current carrying circular loop of radius R?
View SolutionThe moment of inertia of a circular loop of radius R, at a distance of R/2 around a rotating axis parallel to horizontal diameter of loop is
View SolutionA square loop of sides L is placed at centre of a circular loop of radius r (r << L) such that they are coplanar, then mutual inductance between both loop is
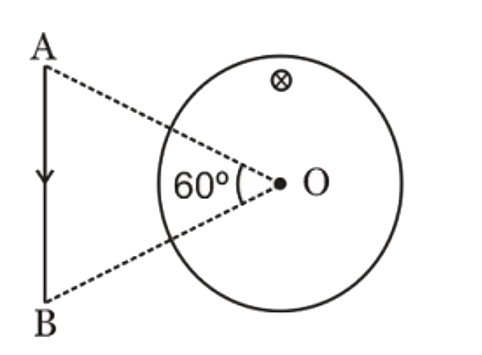
View SolutionA very long cylindrical wire is carrying a current I0 distriuted uniformly over its cross-section area. O is the centre of the cross-section of the wire and the direction of current in into the plane of the figure. The value ∫BA→B.→dl along the path AB (from A to B ) is
View SolutionA current − carrying circular loop of radius R is placed in the XY− plane with centre at the origin. Half of the loop with x>0 is now bent so that is now lies in the YZ− plane
View SolutionA current i is uniformly distributed over the cross section of a long hollow cylinderical wire of inner radius R1 and outer radius R2. Magnetic field B varies with distance r form the axis of the cylinder is
View Solution
