A deadweight suspended from a weightless spring extends it by Δx=9.8cm. What will be the oscillation period of the dead weight when it is pushed slightly in the vertical direction ? The logarithmic damped decrement is equal to λ=3.1
The Eqn of the dead weight is
m..x+2βm.x+mω20x=mg
so Δx=gω20 or ω20=gΔ.x
Now λ=2πβω=2πβ√ω20−β2 or ω0√ω20−β2=√1+(λ2π)2
Thus T=2π√ω20−β2=2πω0√1+(λ2π)2
=2π√Δxg√1+(λ2π)2=√Δxg(4π2+λ2)=0.70sec.
Topper's Solved these Questions
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electric Oscillations
56 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Elastic Waves
39 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Exercise
2 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics
49 Videos
Similar Questions
A ball of mass m when suspended by a spring stretches the latter by Δl. Due to external vertical lforce varying according to a harmonic law with amplitude F0 the ball performs forced oscillations. The logarighmic damping decrement if equal to λ. Neglecting the mass the spring, find the angular frequency of the external force at which the displacemetn amplitude of the ball is maximum. What is the magnitude of that amplitude ?
View SolutionA particle was displaced from the equlibrium position by a distance l=1.0cm and then left along . What is the distance that the particle covers in the process of oscillations till the complete stop, if the logarithmic damping decrement is equal to λ=0.020?
View Solution
Knowledge Check
If the same weight is suspended from three springs having length in the ratio 1 : 3 : 5 , the period of oscillations shall be the ratio of
A1:3:5B1:√3:√5C15:5:3D1:1√3:1√15When a body is suspended from two light springs separately, the periods of vertical oscillations are T1 and T2. When the same body is suspended from the two spring connected in series, the period will be
AT1+T2B√T1T2C√T21+T222D√T21+T22Consider the plane of the paper to be vertical plane with direction of 'g' as shown in the figure. A rod (MM') of mass 'M' and carrying a current I. The rod is suspended vertically through two insulated spring of spring constant K at two ends. A uniform magnetic field is applied perpendicular to the plane of the paper such that the potential energy stored in the spring, in equilibrium position is zero. If the rod is slightly displaced in the vertically direction from the position of equilibrium, then the time period of oscillation is
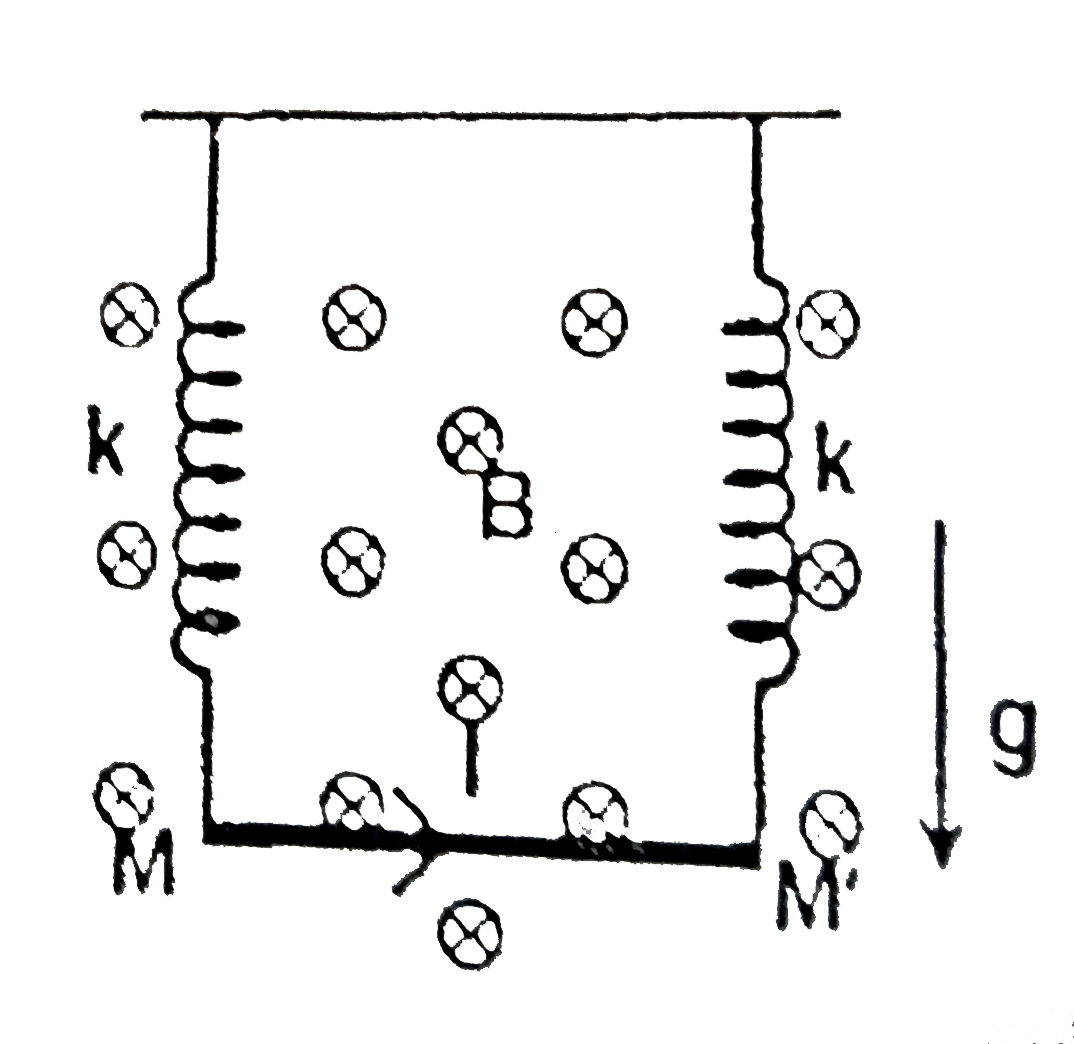 A2π√mKB2π√m2KC2π√K2mD2π√mK⋅mgIlB
A2π√mKB2π√m2KC2π√K2mD2π√mK⋅mgIlB
A uniform disc of radius R=13cm can rotate about a horizontal axis perpendicular to its plane and passing through the edge of the disc. Find the period of small oscillations of that disc if the logarithmic damping decrement is eqal to λ=1.00.
View SolutionA disc A of radius R suspended by an elastic threat between two stationary plane ( figure ) performs torsional oscillations about its axis OO′ . The moment of inertia of the disc relative to that axis is equal to I, the clearance between the disc and each of the planes is equal to h, with h<<R. Find the viscosity of the gas surrounding the disc A if the oscilaltion period of the disc equals T and the logarithmic damping decrement, λ.

View SolutionAn external harmonic force F whose frequency can be varied, with amplitude maintained constant, acts in a vertical direction on a ball suspended by a weightless spring. The damping coefficient is η times less than the natural oscillation frequency ω0 of the ball. How much, in per cent, does the mean power (:P:) developed differ from the maximum mean power (:P:)max? Averaging is performed over one oscillation period.
View SolutionWhen a weight of 2kg is suspended from a spring, its length increases by 3 cm. If the weight is further pulled down by 12 cm and then released, it executes S.H.M. What will be the period of oscillation of the arrangement ? Also calculate the potential energy of the spring .
View Solution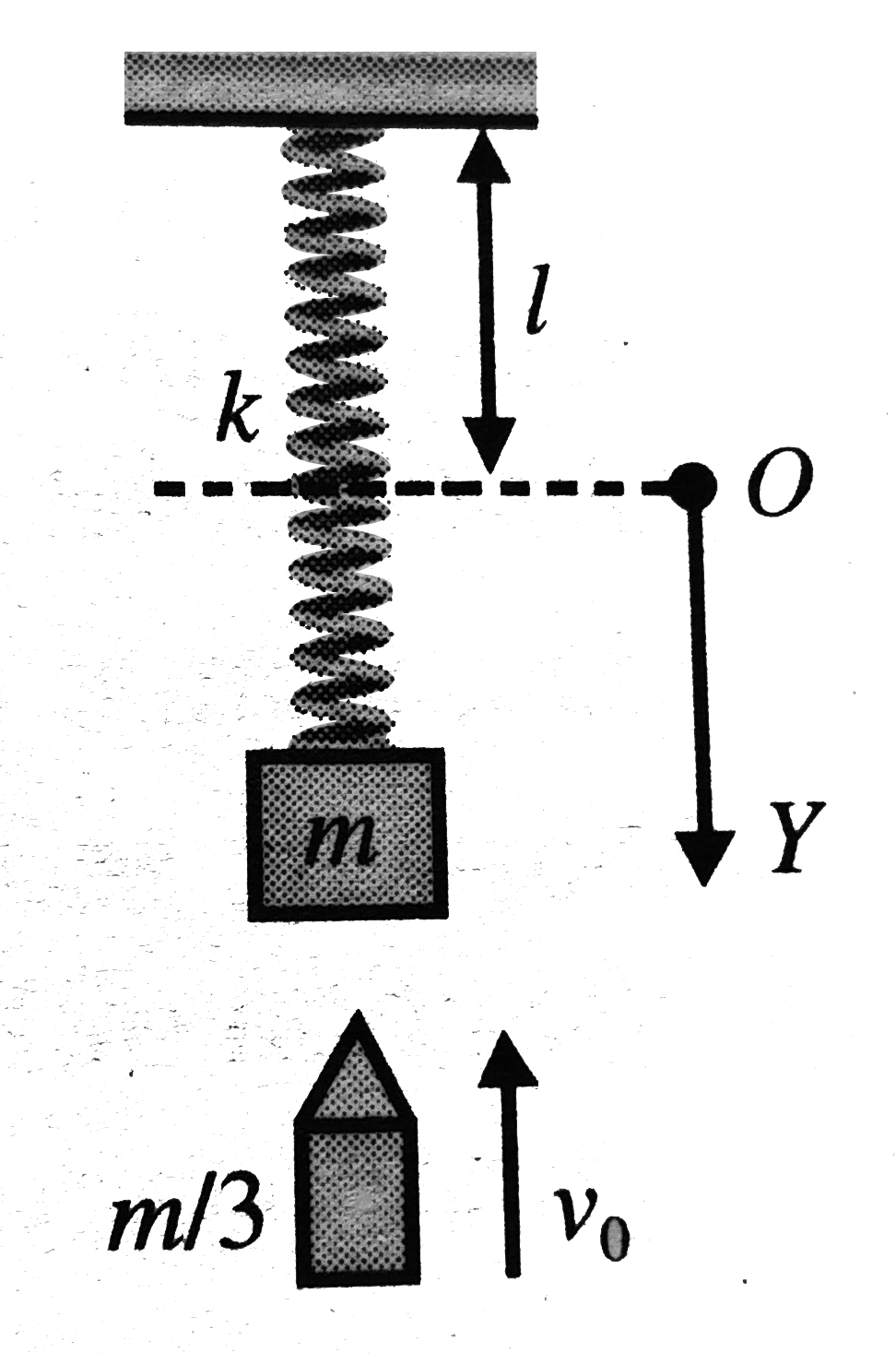
A block of mass m is suspended from one end of a light spring as shown. The origin O is considered at distance equal to natural length of the spring from the ceiling and vertical downwards direction as positive y-axis. When the system is in equilibrium a bullet of mass m3 moving in vertical up wards direction with velocity v0 strikes the block and embeds into it. As a result, the block (with bullet embedded into it) moves up and start oscillating. Based on the given information, answer the following question:
Q. The amplitude of oscillation would be
View Solution
